Аксиоматическое исчисление высказываний

Следует проводить различие между системами с конечным множеством аксиом (системы с аксиомами) и бесконечным множеством аксиом (системы со схемами аксиом). Аксиомой в символической логике называют формулу языка. В пропозициональной логике в качестве аксиомы можно рассматривать формулу 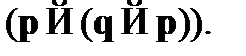Схема аксиом – это выражение метаязыка, которое по сути является множеством формул определенной структуры. Примером может служить выражение 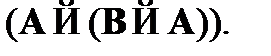Возможны разные системы, представляющие собой формализацию одной и той же пропозициональной логики.

Алфавит и понятие формулы в строящемся ниже исчислении AP – аксиоматическом пропозициональном исчислении – полностью совпадают с алфавитом и понятием формулы, введенных для логики высказываний.

Аксиомы

A1. 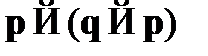– закон утверждения консеквента;

A2. 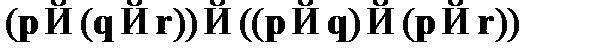– закон самодистрибутивности импликации;

A3. 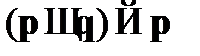– закон удаления конъюнкции₁;

A4. 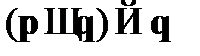– закон удаления конъюнкции₂;

A5. 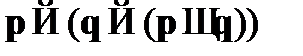– закон введения конъюнкции;

A6. 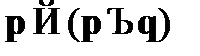– закон введения дизъюнкции₁;

A7. 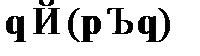– закон введения дизъюнкции₂;

A8. 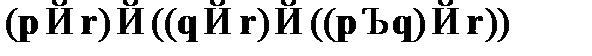– закон исключения дизъюнкции (рассуждение по случаям);

A9. 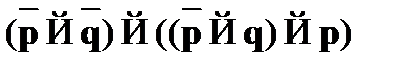– закон введения отрицания (доказательство от противного);

A10. 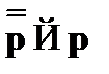– закон исключения отрицания.

Правила вывода: 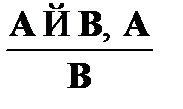– правило modus ponens;

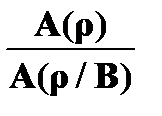– правило подстановки.

В данных правилах символами A и B обозначаются схемы аксиом. В правиле подстановки символом « r » обозначается любая пропозициональная переменная. Само правило позволяет формуле A везде, где встречается переменная r, подставить вместо нее произвольную формулу B.

Доказательством в аксиоматическом исчислении высказываний называют непустую конечную линейно упорядоченную последовательность формул 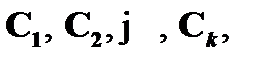каждая из которых является либо аксиомой, либо была получена из предыдущих по одному
из правил вывода. Последняя формула в последовательности, как и в случае натурального исчисления высказываний, называется доказуемой формулой или теоремой. Тот факт, что некоторая формула A является теоремой, фиксируется посредством метаутверждения 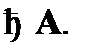При этом последовательность, состоящая из одной формулы (аксиомы), является доказательством этой формулы. Таким образом, любая аксиома – одновременно теорема.

Пример 1. Рассмотрим доказательство формулы 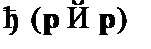в исчислении высказываний
с аксиомами:

(1) 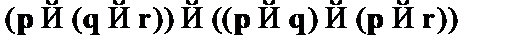– A2 (закон самодистрибутивности импликации);

(2) 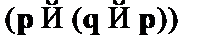– A1 (закон консеквента);

(3) 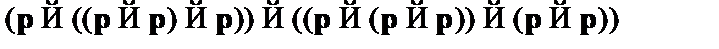– правила подстановк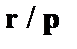и и 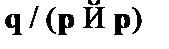, (1);

(4) 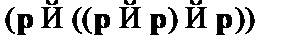– правило подстановки 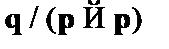, (2);

(5) 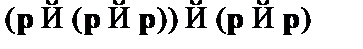– из (3) и (4) по правилу modus ponens;

(6) 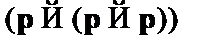– правило подстановки 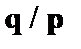к (2);

(7) 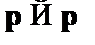– из (5) и (6) по правилу modus ponens.

В данном доказательстве на первом и втором шаге были взяты аксиомы A2 и A1. Третья, четвертая и шестая формулы были получены с применением правила подстановки. Антецендент третьей формулы совпадает с четвертой формулой, что позволило на пятом шаге применить правило modus ponens. Антецендент пятой формулы совпадает с шестой формулой, полученной по правилу подстановки из закона консеквента (A1), что позволило на последнем шаге применить modus ponens к пятой и шестой формулам, получив формулу 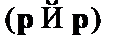. Так как последняя формула последовательности графически совпадает с доказываемой формулой, то теорему следует считать доказанной.

Построение исчисления высказываний со схемами аксиом строится по тому же самому принципу.Исчисление со схемами аксиом является модификацией рассмотренного выше исчисления и содержит бесконечное число аксиом. Модификация состоит в том, что каждая из рассмотренных аксиом заменяется бесконечным множеством аксиом одной и той же структуры. Каждое такое множество представимо некоторой схемой аксиом, которая как раз и задает их общую структуру.

Основные схемы аксиом

CA1. 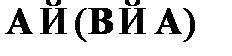– схема утверждения консеквента;

CA2. 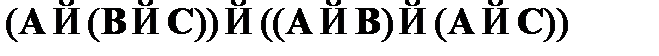– схема самодистрибутивности импликации;

CA3. 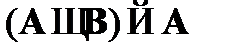– схема исключения конъюнкции;

CA4. 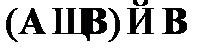– схема исключения конъюнкции;

CA5. – схема введения конъюнкции;

CA6. 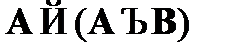– схема введения дизъюнкции;

CA7. 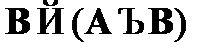– схема введения дизъюнкции;

CA8. 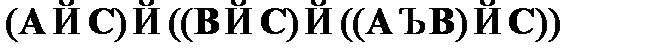– схема исключения дизъюнкции;

CA9. 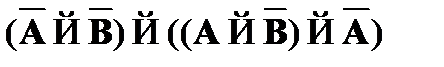– схема введения отрицания;

CA10. 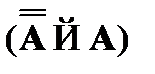– схема исключения отрицания.

Правила вывода.Единственным правилом в исчислении высказываний со схемами аксиом является уже знакомое нам правило modus ponens. Правило подстановки в данном случае оказывается ненужным. Однако исчисление высказываний с аксиомами и исчисление высказываний со схемами аксиом являются дедуктивно эквивалентными.

Выводом формулы B из множества допущений (посылок) Г в системе исчисления высказываний со схемами аксиом является непустая, конечная последовательность формул 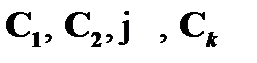, каждая из которых есть либо допущение из Г, или аксиома, или формула, полученная из предыдущих по правилу modus ponens. Таким образом, если формулы 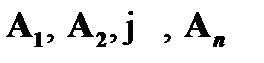– это посылки вывода 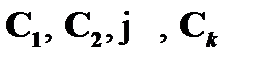, а последняя формула 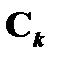графически совпадает с формулой B, то говорят, что формула B выводима из посылок 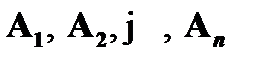. Схематически это записывается в виде выражения 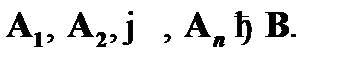Доказательством называется вывод из пустого множества допущений.

В.А. Бочаров и В.И. Маркин указывают на то, что отношение выводимости обладает следующими важными свойствами:

1) 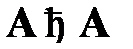(рефлексивность);

2) 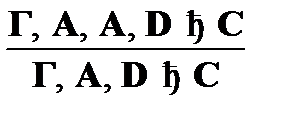(сокращение);

3) 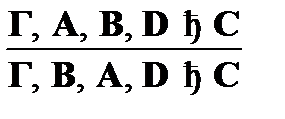(перестановка);

4) 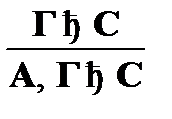(утончение);

5) 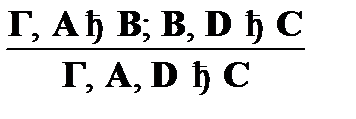(сечение) [15].

Пример 2. Рассмотрим доказательства в исчислении высказываний со схемами аксиом формулы, выражающей закон обратной транзитивности :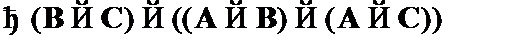

(1) 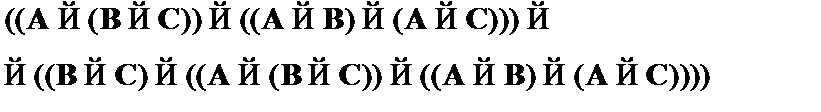– частный случай CA1;

(2) 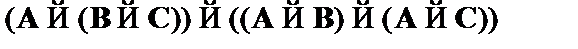– схема аксиом CA2;

(3) – modus ponens к (1), (2);

(4) 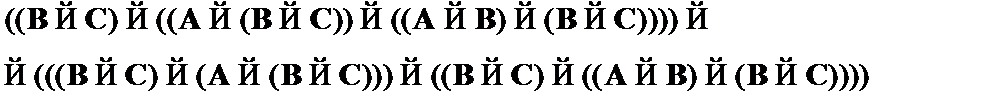– частный случай CA2;

(5) 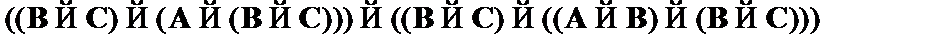– modus ponens к (4), (3);

(6) 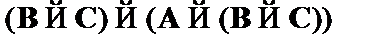– частный случай CA1;

(7) 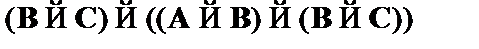– modus ponens к (5), (6).

Пример 3. Рассмотрим доказательство формулы закона транзитивности :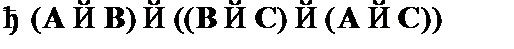

(1) 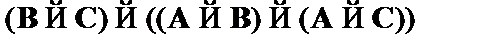– закон обратной транзитивности;

(2) 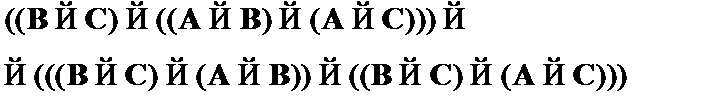– частный случай CA2;

(3) 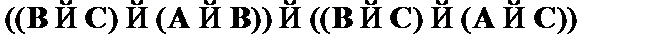– modus ponens к (2), (1);

(4) 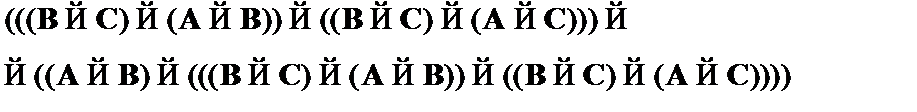– частный случай CA1;

(5) 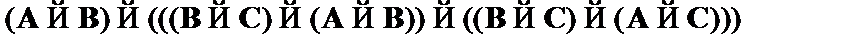– modus ponens к (4), (3);

(6) 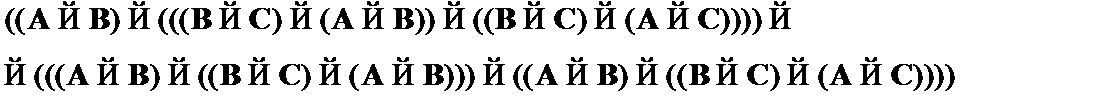– частный случай CA2;

(7) 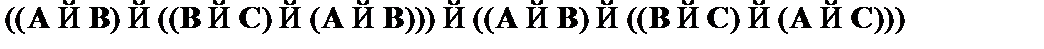– modus ponens к (5), (6);

(8) 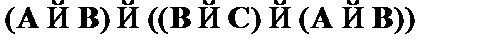– частный случай CA1;

(9) 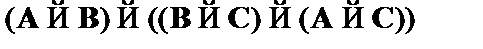– modus ponens к (7), (8).

В данном примере первая формула не является аксиомой, что нельзя рассматривать как нарушение правил, так как доказательство формулы, открывающей последовательность, всегда можно привести. Также данный пример показывает всю сложность обоснования теорем в аксиоматических исчислениях.

Вывод и доказательство в аксиоматическом исчислении высказываний представляет собой сложную задачу. Главная сложность заключается в подборе нужных аксиом. Вывод и доказательство теорем упростится, если будет обоснована метатеорема дедукции: если из множества формул Г и формулы A выводима формула B 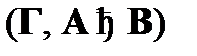, то из множества формул Г выводима формула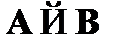 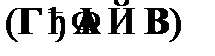. Символически данное определение может быть записано так:

.

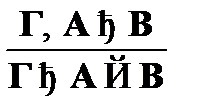Метатеорема: в исчислении высказываний со схемами аксиом справедлива теорема дедукции.

Доказательство ведется методом возвратной индукции по длине вывода. Индуктивное допущение: допустим, имеется упорядоченное множество объектов (< m, ..., n > ) таких, что для всех объектов m (при m < n) выполнимо свойство 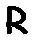, т. е. верно 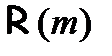. Индуктивное допущение может быть выражено посредством записи: 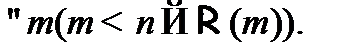В случае если данное допущение является истинным, то свойство будет выполняться и для n-го объекта множества, т. е. пытаются доказать утверждение 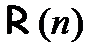. Переход от допущения 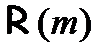к доказательству 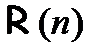называется индуктивным шагом. Индуктивный шаг обозначается при помощи записи: . Если эти рассуждения проделаны успешно, то считают, что свойство 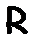выполняется для любого объекта из данного множества. В формализованной записи данный принцип возвратной индукции имеет следующий вид:

.

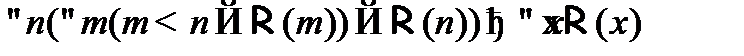В случае нашей метатеоремы упорядоченным множеством объектов будут формулы, входящие в вывод вида 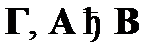. Знаками m и n обозначаются формулы вывода
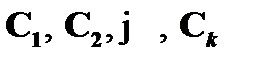( ) с номерами m и n. Свойством Â является сама теорема дедукции. Формулы, входящие в множество Г, и формула A – посылки вывода; формулы, которые входят в множество Г, называются неустранимыми посылками, так как они должны быть сохранены в результирующем выводе 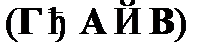. Формула A называется устраняемой посылкой, так как в результирующем выводе ее нет среди посылок.

Доказательство метатеоремы. Рассмотрим некоторый вывод ( 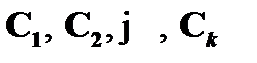) формулы B из посылок Г и A. Индуктивное допущение: для всех формул с номером m < n
в этом выводе справедливо метаутверждени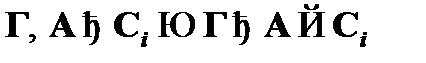е: , где 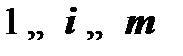. Покажем теперь, что данное свойство будет обязательно выполнено и для формулы C_n (индуктивный шаг).

Дальнейшее рассуждение зависит от того, чем является формула C_n в исходном выводе ( 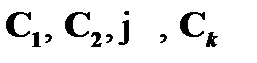) формулы B из посылок Г и A. Согласно понятию вывода, формула C_n может быть или аксиомой, или неустраняемой посылкой из Г, или устраняемой посылкой A, или, наконец, может быть получена из предыдущих формул ( 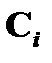и 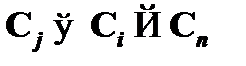, где i и j 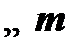) по правилу modus ponens. В соответствии с этим для доказательства необходимо показать, что теорема дедукции ( 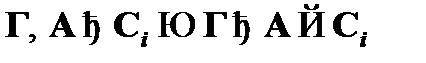) верна для каждого из указанных случаев.

I. Предположим, что C_n в исходном выводе 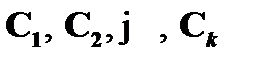формулы B из посылок Г и A графически совпадает с произвольной аксиомой. Тогда C_n доказуема и является теоремой( 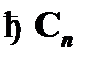), так как доказуема в исчислении высказываний со схемами аксиом, и, следовательно, в соответствии со свойством утончения имеет место 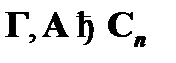. В таком случае требуется показать наличие вывода 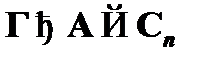, в котором формула 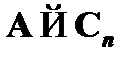выводится только из множества посылок Г без использования неустранимой посылки A. Для этого достаточно рассмотреть следующую последовательность формул:

(1) 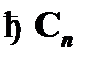– аксиома;

(2) 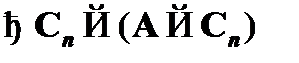– частный случай схемы CA1 (схема утверждения консеквента);

(3) 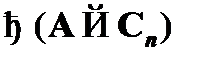– правило modus ponens к формулам (1) и (2).

Данные формулы последовательности показывают, что 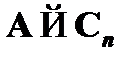является теоремой исчисления высказываний со схемами аксиом ( 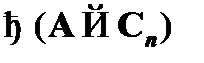), а значит, по свойству утончения, должен существовать вывод вида 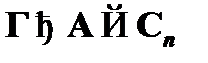, что и доказывает метаутверждение 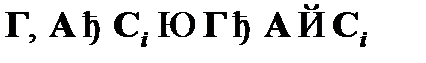для этого случая.

II. Далее предположим, что C_n – произвольная неустранимая посылка. Таким образом, 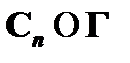, и для него верно утверждение 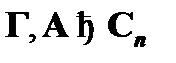, а следовательно, и вывод 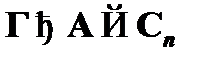. Это видно из следующей последовательности:

(1) 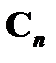, где 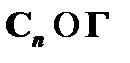– следует из понятия неустранимой посылки;

(2) 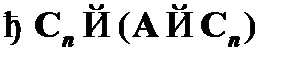– аксиома CA1;

(3) 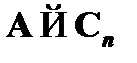– правило modus ponens к (1) и (2).

Таким образом, формула 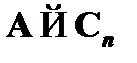выводима из формулы 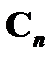, т. е. имеем 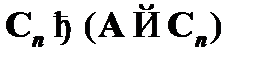. Но, как нам известно, 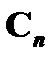является неустранимой посылкой ( 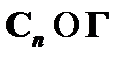), а значит, 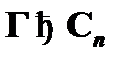, и по сечению мы можем получить 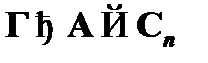. Следовательно, метаутверждение для данного случая также является верным.

III. Допустим, что имеется графическое совпадение 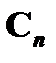с устраняемой посылкой A ( 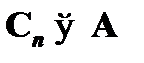). В силу графического равенства вывод 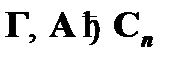принимает вид 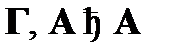. Для того чтобы показать наличие вывода вида 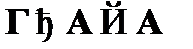, необходимо рассмотреть последовательность формул:

(1) 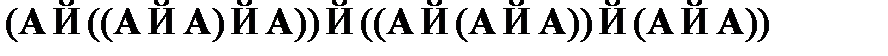– частный случай схемы аксиом CA2;

(2) 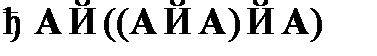– частный случай схемы CA1;

(3) 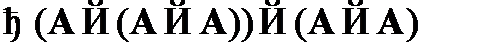– из (1) и (2) по правилу modus ponens;

(4) 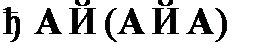– частный случай CA1;

(5) 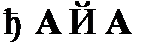– из (3) и (4) по правилу modus ponens.

Таким образом, доказано, что является теоремой исчисления высказываний со схемами аксиом, а значит, (по утончению) должен существовать вывод 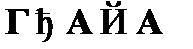, что и доказывает метаутверждение для этого случая.

IV. Наконец, предположим, что формула 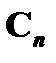получена из предыдущих формул 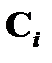и 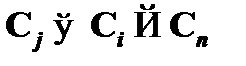по правилу modus ponens. Так как формулы 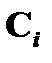и 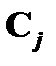предшествуют формуле 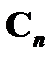, то их номер в последовательности ( i и j ) меньше n. Это означает, что по индуктивному предположению для формулы 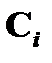имеет место 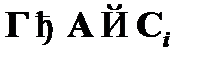, а для формулы 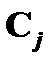будет иметь место 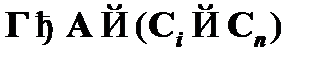. Для того чтобы показать наличие вывода вида 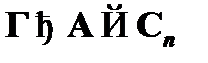, необходимо рассмотреть последовательность формул:

(1) 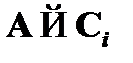– выполнимость свойства 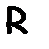для формулы ;

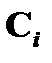(2) 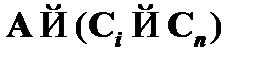– выполнимость свойства для формулы ;

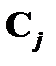(3) 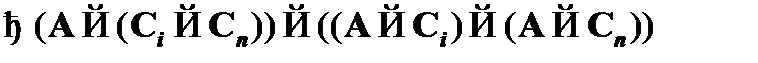– частный случай схемы аксиом CA2;

(4) 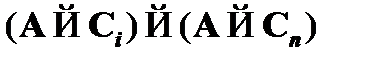– применение правила modus ponens к (3) и (2);

(5) 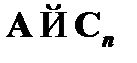– применение правила modus ponens к (4) и (1).

Данная последовательность доказывает выводимость 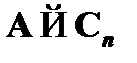из посылок 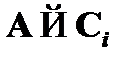и 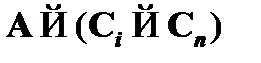, т. е. обосновывает вывод вида 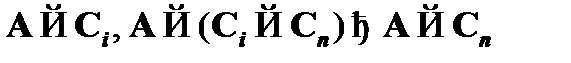. По индуктивному допущению для 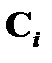имеет место 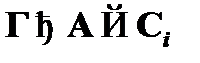, а для формулы 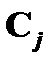– 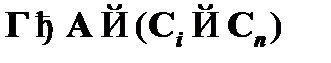. Последовательно применив сечение, получаем 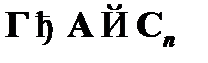. Таким образом, индуктивный шаг следует считать доказанным. Тем самым доказана теорема дедукции.

Прямы и непрямые правила вывода. Прямые правила вывода указывают на непосредственную выводимость некоторой формулы B из множества формул (посылок правила) 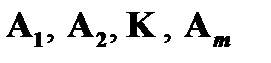(где 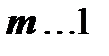). Непрямое правило позволяет непосредственно заключить от наличия некоторых выводимостей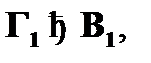 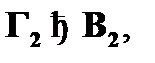..., 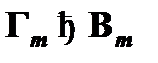к наличию определенной выводимости 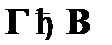(где 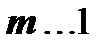). Правило, соответствующее теореме дедукции, представляет собой простое сокращение вывода. Однако введение непрямых правил в систему создает определенные трудности. Понимая выводы как последовательности формул, необходимо в каждом случае применения правила дедукции отмечать тот факт, что формула 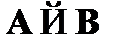выводится не из всех посылок исходного вывода 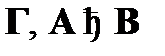, а лишь из множества Г. Применяя теорему
дедукции, необходимо каждый раз исключать из последовательности все формулы, выведенные на основе допущения.

Рассмотрим доказательство формулы вида :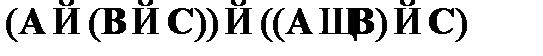

(1) 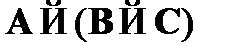– допущение;

(2) 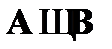– допущение;

(3) 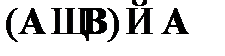– CA3 (схема исключения конъюнкции);

(4) A – по правилу modusponensиз (3), (2);

(5) 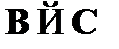– по правилу modusponensиз (1), (4);

(6) 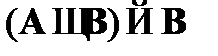– CA4 (схема исключения конъюнкции);

(7) B – по правилу modusponensиз (6), (2);

(8) C – по правилу modusponensиз (5), (7);

(9) 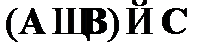– теорема дедукции к (2)–(8);

(10) 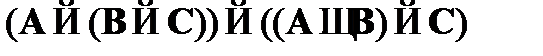– теорема дедукции к (1)–(9).

Вертикальная сплошная черта указывает в данном случае на шаги вывода, следующие за допущением, к которым применяется теорема дедукции. Отмеченные шаги исключаются из дальнейшего рассуждения.