
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Моделирование в динамике материальной точки
И системы частиц Согласно фундаментальной концепции Ньютона свойства природы в больших масштабах полностью определяются её микроскопическим строением. Поэтому изучение природы было бы естественно начинать с нахождения подлинных «кирпичиков» мироздания и установления характеристик, определяющих их состояние и движение. Однако свойства реальных элементарных объектов нам пока неизвестны. В этих условиях, следуя Ньютону, вместо реальных объектов природы на роль таких «кирпичиков» целесообразно выбирать их идеализированную модель [2]. Наиболее подходящей для этого является модель частицы, или корпускулы, интуитивное представление о которой имеет каждый человек. Под ней, как правило, подразумевается малая доля любого материального объекта. Характерные особенности этой модели мы начали раскрывать в предыдущем семестре (пропедевтический курс физики). Выделенная роль модели частицы в описании природы определяется двумя обстоятельствами. Во-первых, эта модель универсальна, ибо в определённых условиях и реальная элементарная частица (например, электрон), и пылинка, и биллиардный шар, и планета, и галактика могут рассматриваться как частицы. Во-вторых, она предельно проста, поскольку состояние частицы минимально фиксируется всего двумя параметрами, определяющими все остальные её характеристики До сего момента, в частности, в работе [3], мы говорили о модели свободной частицы. Однако для реальных ситуаций, к рассмотрению которых мы приступаем, частицы испытывает непрерывное внешнее воздействие, но и к ним, всё же, применима модель частицы [2]. Это означает возможность моделирования материальных объектов «несвободными» частицами, характеристики состояния которых изменяются со временем. Такая модель обладает рядом преимуществ. Во-первых, она позволяет использовать такую частицу в качестве «зонда» при исследовании характеристик внешних воздействий и их взаимосвязей со свойствами пространства и времени. Во-вторых, в модели «несвободной» частицы известные характеристики состояния свободной частицы не остаются со временем без изменения. В связи с этим представляет интерес установление объективных характеристик внешнего воздействия на частицу, и открытие и применение законов, управляющих изменением характеристик состояния частицы со временем. Рассуждая о проблемах исследования довольно простых систем – либо о свободных частицах, либо об одиночной частице, испытывающей непрерывное воздействие со стороны окружающих её массивных тел, мы, вместе с тем, не должны забывать, что в природе гораздо чаще встречаются совокупности материальных объектов, каждый из которых можно моделировать частицей. Такова, например, Солнечная система или рассмотренная ранее нами модель идеального газа. Общей особенностью таких совокупностей является взаимодействие составляющих их объектов между собой либо кратковременно (например, в газах), либо непрерывно (планетные системы). Возможно ли описать подобные совокупности материальных объектов, опираясь на введённые модели свободной и несвободной частицы? Для упрощения аналитического решения задачи будем рассматривать только изолированные совокупности частиц. В то же время не будем забывать, изолированная система взаимодействующих частиц, взятая сама по себе, – это обобщение модели свободной частицы, но лишь в те моменты, когда её размерами можно пренебречь. Таким образом, модель изолированной системы взаимодействующих частиц имеет то преимущество, что её свойства жёстко связаны со свойствами пространства и времени, описываемыми фундаментальными законами сохранения. Опираясь на эти законы можно описать движение частиц при различных способах их взаимодействия и движения в изолированной системе, а также движение самой системы как целого. При этом у нас появляется возможность постепенного перехода от кратковременного взаимодействия, проявляющегося внутри системы, к непрерывному взаимодействию, характерному для движения системы как целого. Ранее, в работе [3, гл. 4; 5] мы уже использовали процессы кратковременного взаимодействия частиц, или, иначе, столкновения, для введения ряда фундаментальных величин, характеризующих свободную частицу. Переход от свободной частицы к изолированной системе частиц, взаимодействующих кратковременно, позволил нам сформулировать фундаментальные законы сохранения импульса и энергии для этой системы. Оказалось, знание одних только фундаментальных законов сохранения позволяет описать многие свойства изолированной системы частиц, взаимодействующих кратковременно, даже при отсутствии какой-либо информации о деталях взаимодействия. В связи с этим содержание данной главы сводится к динамике частиц и введению характеристик не только для одиночной частицы, но и для системы частиц, определяющих состояние и движение системы как целого. Следует также обратить внимание на то, что в работе [3, с. 15] нами были предприняты усилия по рассмотрению динамики прямолинейного движения тел; здесь, однако, предметом исследования была физическая причина, обусловливающая тот или иной характер движения тела. Однако движущееся тело, как мы знаем, состоит из большого ансамбля частиц, материальных точек – молекул или атомов. В связи с этим естественно возникает вопрос, а «работают» ли законы динамики Ньютона при рассмотрении движения единичной частицы и каковы предельные размеры рассматриваемой частицы? Частично убедиться в этом нам удалось при рассмотрении колебательных процессов, механики сплошных сред и статистических методов исследования в работе [3, гл. 3; 4; 5].
1.2. Пространственные и временные отношения, Прежде чем приступить к рассмотрению обозначенных в данной главе вопросов, уместно кратко остановиться на однородности и изотропности пространства и однородности времени; частично эти вопросы были подняты в предыдущем семестре [3, с.6–8]. Однако к их пониманию сейчас мы подготовлены лучше, поскольку выработанное на данный момент на основании повседневного опыта интуитивное представление о пространстве, времени и движении позволяет утверждать: пространство – это порядок взаимного расположения материальных объектов, выражаемый словами ближе–дальше; время – это порядок сменяющих друг друга состояний материальных объектов, выражаемый словами раньше–позже. Отсюда немедленно следует первое общее свойство пространства и времени – их относительность. Вместе с тем, говорить о пространстве и о времени без материальных объектов, без каких-то процессов не имеет смысла. Второе общее свойство пространства и времени – их взаимозависимость. Не существует пространственных и временных отношений по отдельности. В природе любой процесс происходит в некоторой области пространства, а материальный объект как-то изменяется со временем. Поэтому имеет смысл говорить лишь о единых пространственно-временных отношениях между событиями, характеризующими – где и когда что-то происходит в природе. Каково объективное содержание этих понятий и как их описывать количественно – наша цель. Пространственные и временные отношения относятся к наиболее фундаментальным понятиям и их невозможно свести к другим, более простым. В физике такие понятия принято определять путём указания процедуры их измерения. Будем пока считать, что эти отношения друг от друга не зависят, и дадим их определения, начав с временных отношений. С этой целью введём эталонный процесс, называемый часами. В качестве такового можно использовать любой периодический процесс, в котором с достаточной точностью повторяется одно и то же состояние материального объекта. Примеры подобных процессов человечество «поймало» из повседневной жизни: движение Земли вокруг оси Солнца; пульс человека, колебания математического маятника и т. п. Измерение длительности любого процесса состоит в его сравнении с длительностью эталонного процесса, играющего роль деления шкалы времени.
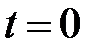 или на одномерной шкале – оси времени t временную координату или на одномерной шкале – оси времени t временную координату 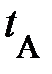 (рис. 1.1, нижняя ось времени). Естественно ожидать, моменты времени одного и того же события относительны (рис. 1.1, нижняя ось времени). Естественно ожидать, моменты времени одного и того же события относительны 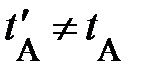 (рис.1.1, верхняя ось времени). Они «чувствительны» к выбору начала отсчёта времени, так что сами по себе не являются объективными характеристиками времени; начало отсчёта верхней оси времени не совпадает с началом отсчёта нижней оси времени (рис. 1.1., обратили внимание? ). Например, в момент Вашего появления читатель на территории России Ваши дальние родственники в Европе зафиксировали (поставили в соответствие) другое число – момент времени события или временную координату (рис.1.1, верхняя ось времени). Они «чувствительны» к выбору начала отсчёта времени, так что сами по себе не являются объективными характеристиками времени; начало отсчёта верхней оси времени не совпадает с началом отсчёта нижней оси времени (рис. 1.1., обратили внимание? ). Например, в момент Вашего появления читатель на территории России Ваши дальние родственники в Европе зафиксировали (поставили в соответствие) другое число – момент времени события или временную координату 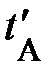 на одномерной шкале – оси времени на одномерной шкале – оси времени 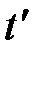 ; можете воспользоваться просторами России, проявится то же самое. ; можете воспользоваться просторами России, проявится то же самое.
Из приведённых выше рассуждений следует, объективной характеристикой временных отношений может служить лишь промежуток времени
Переходя с символического языка математической записи на знаковый (словесный) язык, можно сказать, промежутки времени инвариантны, неизменны по отношению к выбору начала отсчёта времени. В этой аналитической записи, представленной знаковым языком, отражается важнейшее свойство времени – его однородность (см. рис. 1.1). Разобравшись с математическим описанием временных отношений, перейдём к рассмотрению пространственных отношений. Разумеется, в обозначенной нами задаче для поступательного движения частицы достаточно пока определить пространственные отношения вдоль прямой, по которой происходит это движение. Для этого придётся ввести эталонный объект, в качестве которого можно использовать любой материальный объект, размер которого фиксирован с достаточной точностью; например, линейка, метр и т.п.
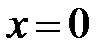 (рис. 1.2, ось Х слева), любой другой материальной точке или частице на одномерной шкале пространственной оси Х можно поставить в соответствие одно число – пространственную координату события (рис. 1.2, ось Х слева), любой другой материальной точке или частице на одномерной шкале пространственной оси Х можно поставить в соответствие одно число – пространственную координату события 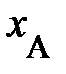 , например, появлению вас, читатель, на территории северного района. Очевидно, пространственные координаты одного и того же события А относительны. Они «чувствительны» к выбору начала отсчёта на пространственной оси, например, ось , например, появлению вас, читатель, на территории северного района. Очевидно, пространственные координаты одного и того же события А относительны. Они «чувствительны» к выбору начала отсчёта на пространственной оси, например, ось 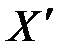 (рис. 1.2., справа) (рис. 1.2., справа) 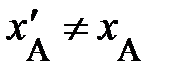 ; следовательно, сами по себе пространственные координаты не являются объективными характеристиками пространства. Действительно, событию вашего появления на территории северного района родственниками южного района будет приписана пространственная координата ; следовательно, сами по себе пространственные координаты не являются объективными характеристиками пространства. Действительно, событию вашего появления на территории северного района родственниками южного района будет приписана пространственная координата 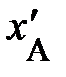 . .
Возникшие трудности могут быть преодолены, если мы поступим так же, как это было проделано при математическом описании временных отношений (1.1). Действительно, если воспользоваться понятием расстояния
Из этой аналитической записи и рис. 1.2 следует, значение расстояния
1.3. Характеристики прямолинейного движения. Приведённые выше описания временных и пространственных отношений можно считать независимыми лишь условно. В реальности необходимость анализа поведения материальных объектов в пространстве с течением времени неизбежно приводит к переходу к взаимосвязанным пространственно-временным отношениям. Их математическое описание можно получить, объединив введённые описания отношений (рис. 1.1 и 1.2) вдоль осей х и t соответственно. Для этого мы связывали декартову систему координат с телом отсчёта и «местными» часами [3], что позволило нам ввести понятие системы отсчёта. В этом случае каждому событию, характеризующему где и когда находится частица (тело), в системе отсчёта S (рис. 1.3) соответствует мировая точка А или два числа Действительно, понятия событие, мировая точка, мир событий в повседневной жизни неявно использует каждый человек. Ранее без них мы не могли описать даже столь простое явление, как прямолинейное движение. В частности, одного указания на то, что траектория частицы – это прямая, например, ось Х, для описания частицы недостаточно. Вдоль одной и той же прямой частица может двигаться направо или налево, равномерно или неравномерно (рис. 1.3) и т. п. Поэтому для последовательного описания прямолинейного движения необходимо использовать «двумерный» мир событий. В нём с прямолинейным движением частицы вдоль оси Х сопоставляется непрерывная совокупность событий, указывающих, где и когда находится движущийся объект. По сути на плоскости Хt прямолинейное движение изображается непрерывной кривой Итак, физики, опираясь на математический аппарат (пусть и простой в нашем случае), показали, характеристика быстроты движения – скорость – определяется через пространственные и временные отношения, определение которых в свою очередь связано с движением [2, 6]. Это говорит о том, что всякое раздельное рассмотрение пространственных и временных отношений (даже в неподвижной системе отсчёта) является непоследовательным. Окружающая же нас природа существует в едином многообразии – мире событий, в котором понятие пространства, времени и движения взаимосвязаны и неразрывны. Говоря здесь для простоты о двумерном мире событий – плоскости Хt – мы в реальности имеем дело не с отношениями вдоль отдельных осей Х и t, а принципиально с отношениями на плоскости Хt. Это целостное двумерное многообразие, на котором заданы как расстояния и промежутки времени, так и любые мировые точки событий, и мировые линии любой формы, соответствующие движению материальных объектов. Какое отношение имеет сказанное выше для вопроса, обозначенного в данной главе? Во-первых, мы убедились в том, что если задан график движения
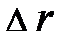 характеризуется одним числом и имеет в данной точке пространства одинаковое значение в любой неподвижной системе отсчёта. Векторная физическая величина – вектор расстояния характеризуется одним числом и имеет в данной точке пространства одинаковое значение в любой неподвижной системе отсчёта. Векторная физическая величина – вектор расстояния 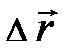 характеризуется численным значением и направлением в пространстве. Вектор расстояния характеризуется численным значением и направлением в пространстве. Вектор расстояния 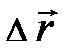 (рис. 1.4) – пример математической величины, обладающей не только численным значением, но и направлением. Графически вектор принято изображать стрелкой, направленной от А к В, а его модуль в двумерном пространстве (для простоты записи) может быть представлен через проекции на координатные оси следующим образом: (рис. 1.4) – пример математической величины, обладающей не только численным значением, но и направлением. Графически вектор принято изображать стрелкой, направленной от А к В, а его модуль в двумерном пространстве (для простоты записи) может быть представлен через проекции на координатные оси следующим образом: 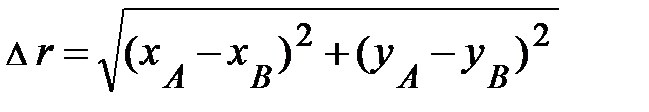 . .
Следует заметить, запись физических законов (в неподвижных системах отсчёта) через скаляры и векторы существенна лишь для установления самих этих законов или для демонстрации каких-то общих объективных свойств. Для практических же целей их целесообразно спроецировать на оси более удобной неподвижной системы отсчёта; этим мы, кстати, и занимаемся при решении задач. Таким образом, свойства однородности и изотропности пространства, позволившие выделить объективные характеристики пространственных отношений, предопределяют наиболее общие свойства любых физических величин, пригодных для объективного описания природы. Вместе с этим законы, записанные в форме математического соотношения, содержащего скаляры и векторы, ковариантны, т е. имеет одинаковый вид в любой неподвижной системе отсчёта.
1.4. Принцип инерции. Импульс как характеристика Обсуждение пространственно-временных отношений позволило прописать поступательное движение частиц (корпускул) и выявить важнейшие характеристики состояния материального объекта { Из опыта известно, характер движения частицы зависит от воздействия на неё окружающих материальных объектов, причём с удалением частицы от них это воздействие убывает. Теперь представим идеализированную ситуацию – частица движется столь удалённо от всех остальных материальных объектов (включая и тело отсчёта), что их воздействием на неё можно вообще пренебречь. Кстати, такую частицу принято называть свободной. В реальных условиях примером движения свободной частицы может служить установившееся движение парашютиста; тяготение Земли компенсируется сопротивлением воздуха. Разумно предположить, в мире событий (§ 1.3) график движения свободной частицы х =х(t) должен быть максимально прост. Изучая форму мировых линий на плоскости Хt(рис. 1.3), нетрудно понять – простейшей формой обладают мировые линии, для которых Закон движения свободной частицы (принцип инерции) был сформулирован ещё в начале XVII в. Г. Галилеем. В современной трактовке, как первый закон Ньютона, принцип инерции читается так: существуют системы отсчёта, в которых любая свободная частица движется равномерно и прямолинейно или покоится. Очевидна его тесная связь с проблемой выбора систем отсчёта, относительно которых должна быть инвариантна (неизменна) форма законов природы, поэтому он оказался первым фундаментальным законом физики. Системы отсчёта, в которых выполняется закон инерции, называются инерциальными; все остальные – неинерциальными. Здесь уместно заметить, несмотря на внешнюю простоту принципа инерции, это одно из крупнейших достижений в истории физики; с этого момента появилась возможность формулировать объективные законы природы, а физика родилась как наука. Из закона инерции следует важный вывод, скорость – это характеристика движения свободной частицы. При наличии же внешнего воздействия это уже не так – разные частицы, двигавшиеся первоначально с одинаковой скоростью, изменяют её по-разному. Это значит, помимо скорости частицам (телам) присуща какая-то характеристика, отличающая одну частицу от другой и играющая роль внутренней характеристики самой материи. Такой универсальной характеристикой материи служит масса. В области привычных для нас скоростей имеет место правило – в одних и тех же условиях более массивное тело способно приобрести меньшую скорость; т. е. оно более инертно. Понятие массы m(инертной) столь же
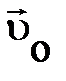 =0 (представлено пунктиром), то частицы 1 и 2 движутся вдоль прямой, а векторы =0 (представлено пунктиром), то частицы 1 и 2 движутся вдоль прямой, а векторы 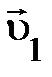 и и 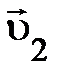 направлены в противоположные стороны (рис. 1.5.). Моделируя распады направлены в противоположные стороны (рис. 1.5.). Моделируя распады
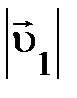 и и 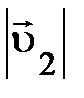 могут изменяться, но их отношение не зависит от самих могут изменяться, но их отношение не зависит от самих 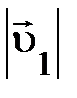 и и 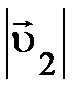 , оставаясь постоянным: , оставаясь постоянным: 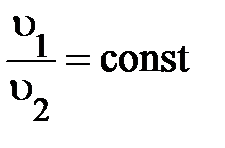 . Кроме того, если исходная частица распалась на две другие частицы, то это отношение измениться, но опять . Кроме того, если исходная частица распалась на две другие частицы, то это отношение измениться, но опять 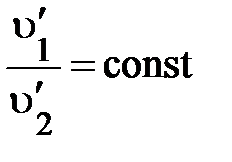 . Очевидно, отношение модулей скоростей образовавшихся частиц характеризует какое-то их внутреннее свойство не связанное непосредственно с движением. Всё это указывает на то, что отношение модулей скоростей частиц, образующихся при распаде покоящейся исходной частицы, обратно пропорционально их массам, характеризующим способность изменять свою скорость в одних и тех же условиях. Аналитически это может быть представлено так: . Очевидно, отношение модулей скоростей образовавшихся частиц характеризует какое-то их внутреннее свойство не связанное непосредственно с движением. Всё это указывает на то, что отношение модулей скоростей частиц, образующихся при распаде покоящейся исходной частицы, обратно пропорционально их массам, характеризующим способность изменять свою скорость в одних и тех же условиях. Аналитически это может быть представлено так:
Несмотря на простоту, утверждение (1.3) не противоречит интуитивным представлениям об инертности – из двух частиц, образовавшихся при распаде, меньшей скоростью (по модулю) обладает частица с большей массой. Оно так же даёт способ измерения инертной массы, например, на борту космического корабля. На практике применяются другие методы (какие? ). Таким образом, масса является «визитной карточкой» частицы – например, элементарной, из которой состоят атомы, молекулы и более крупные тела. Из опыта следует, где бы и когда бы ни была обнаружена подобная частица, её масса остаётся одним и тем же внутренне присущим ей числом. Оно не «чувствительно» к положению частицы в пространстве и к моменту времени её наблюдения. Всё это позволяет предположить, масса – скалярная величина, не зависящая от выбора инерциальной системы отсчёта, а повседневный опыт подсказывает, она обладает свойством аддитивности (складывающиеся): Здесь мы подошли к важному выводу – для всестороннего описания движения свободной частицы необходимо знать не только её скорость В его важности можно убедиться, воспользовавшись двухчастичным распадом (рис. 1.5). Поскольку после распада частицы всегда разлетаются по прямой в противоположные стороны, из формулы 1.3 получаем: Закон сохранения импульса оказывается полезным при обобщении понятия скорости поступательного движения для изолированной системы частиц как целого в тех случаях, когда её нельзя моделировать одной частицей.
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 848; Нарушение авторского права страницы