
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Вычисление момента инерции для простейших тел
В предыдущем параграфе было показано, что момент инерции может быть представлен как произведение массы а. т. т. на квадрат эффективного радиуса оси инерции: В частном случае для системы N частиц с одинаковой массой mi = m средний квадрат расстояния от оси симметрии может быть представлен следующим образом:
и для тонкого обруча радиусом r, когда все Ri = r = const,
Читателю желательно самостоятельно проделать преобразования, поскольку они требуют сопровождения внутренней речью. В частности, нужно не забыть, что mi = m и что запись суммы требует произведения массы m на квадрат расстояния r. Убедились в этом самостоятельно? Было бы неплохо тонкий обруч отобразить на рисунке с обозначением заданных величин.
где dm – элементарная масса стержня, удалённая от оси вращения Z на расстояние r и обладающая моментом инерции dJ = r2× dm. Поскольку плотность материала стержня r одинакова по всей длине, элементарная масса может быть записана: dm = r× dV = r× S× dr; здесь S – площадь поперечного сечения стержня, а dr – длина бесконечно малого элемента стержня массой dm. Подставляя эти значения в уравнение (3.10) приходим к выражению:
Проведя несложные преобразования, пытливый читатель приходит к уравнению вида:
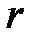 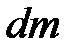 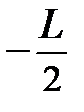 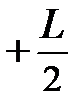 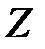 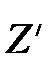 Описание свободного вращения стержня можно упростить, воспользовавшись тем, что угловая скорость wсист.z, будучи общей для всех элементарных масс, не зависит от параллельного переноса оси вращения. Допустим, что наш стержень свободно вращается вокруг оси симметрии Z, проходящей через центр инерции с угловой скоростью wZ. Рассмотрим теперь его вращение вокруг мгновенной оси Z /, параллельной оси Z Описание свободного вращения стержня можно упростить, воспользовавшись тем, что угловая скорость wсист.z, будучи общей для всех элементарных масс, не зависит от параллельного переноса оси вращения. Допустим, что наш стержень свободно вращается вокруг оси симметрии Z, проходящей через центр инерции с угловой скоростью wZ. Рассмотрим теперь его вращение вокруг мгновенной оси Z /, параллельной оси Z (рис. 3.5). В этом случае мы, по существу, имеем дело с комбинацией двух движений – «чистого» вращения вокруг оси Z, характеризуемого моментом импульса Lz = J× wz, и поступательного движения центра инерции стержня по окружности радиуса R = L/2, где R – расстояние между осями Z и Z /, со скоростью uсист = R× wz. Сумму кинетических энергий K поступательного движения и вращения системы частиц в этом случае можно представить в виде:
Входящий в формулу (3.11) эффективный момент инерции Jэф относительно мгновенной оси Z / равен:
где R – расстояние между осями Z и Z /. Формула (3.12) называется формулой Гюйгенса-Штейнера [2] и позволяет вычислять момент инерции для простейших систем. Убедимся в том, что она имеет право на существование. Рассмотрим свободное вращение системы, представленной на рис. 3.5 относительно оси Z /. По формуле Гюйгенса-Штейнера эффективный момент инерции Jэф складывается из момента инерции стержня относительно оси его центра масс Jz и момента инерции центра масс стержня по отношению к оси Z /. Подставляя в выражение (3.12) заданные параметры, приходим к выражению вида: Проверим результат формулы (3.12) Jэф = (1/3)× mL2 через математическую операцию интегрирования. Воспользуемся формулой (3.10),
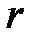 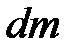 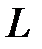 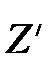 Подставив вместо r верхний предел интегрирования L, читатель придёт к выражению: Подставив вместо r верхний предел интегрирования L, читатель придёт к выражению:
Применяя дифференциально-интегральное исчисление можно вычислить момент инерции для однородного: точечного тела, находящегося на расстоянии R от заданной оси вращения J = mR2; сплошного шара относительно оси, проходящей через его центр J = (2/5)× mR2; полого цилиндра относительно оси, проходящей параллельно его стенкам через центр масс, как разность моментов инерции наружного и внутреннего (отсутствующего) цилиндров J = 1/2m1× R12 – 1/2 m2× R22, или J = 1/2m× (R12 + R22), где m = m1 – m2 есть масса полого цилиндра. Для пытливого читателя следует заметить, при попытке получить конечное выражение учтите, что в выражение массы mi так же входит Ri; может помочь в преобразованиях. Удачи.
Основное уравнение вращения Наши рассуждения в работе [3] и те, которые представлены в предыдущих параграфах, позволяют утверждать, что концепция дальнодействия позволила нам во многих случаях рассматривать вещество как систему взаимодействующих частиц в условиях внешнего воздействия. В свою очередь эти внешние воздействия созданы другими материальными объектами. Естественно, понятие вещества при этом следует трактовать весьма широко. В наших рассуждениях это были: планетная система, кристалл или газ в сосуде. Очевидно, единообразного описания столь различных объектов можно достичь только в рамках какого-то общего приближённого подхода. И контуры его нами были фактически намечены не только в работе [3], но и в предыдущих параграфах. В частности, нам удалось показать, что систему исходных взаимодействующих частиц в определённых условиях можно смоделировать эквивалентной системой независимых «квазичастиц». Следующий шаг, который нам удалось сделать, это переход от модели свободной частицы к модели несвободной частицы, находящейся во внешнем поле. Естественно, модель несвободной «квазичастицы» сложнее модели частицы, поэтому ограничимся анализом лишь простейших систем непрерывно взаимодействующих частиц, которые моделируются изученными выше «квазичастицами». К ним, в частности, относятся «квазичастица» с приведённой массой и центр инерции, с которыми нам приходилось работать и ранее [3]. В предыдущих рассуждениях нам удалось достичь сколько-нибудь полного описания движения материальных объектов только в приближении а. т. т., которому соответствует простейшее предположение об энергии парного взаимодействия: Приступая к изучению движения системы частиц при наличии внешнего воздействия целесообразно начать с введения характеристик такого воздействия. Если оговорённые выше условия выполняются, т. е. к системе применимо приближение а. т. т., то внешнее воздействие на неё сводится, лишь, к воздействию на поступательное движение и вращение системы частиц как целого. В этом случае систему частиц уже нельзя считать изолированной, подобное воздействие непосредственно связано с нарушением свойств однородности и изотропности пространства. В связи с этим за характеристики внешнего воздействия на систему частиц целесообразно выбрать «темп», (быстроту) изменения со временем её фундаментальных физических величин – импульса С этой целью запишем импульс
Здесь И тогда «темп» (быстрота) изменения импульса системы со временем
Аналогично в качестве специфической характеристики внешнего воздействия на вращение системы частиц как целого выберем «темп» изменения со временем момента импульса системы частиц. Аналитически это запишется (см. 3.13):
Поскольку R – радиус-вектор центра инерции является величиной постоянной, то производная от векторного произведения приводит к выражению
и тогда, наконец, мы получаем уравнение (3.15) в виде:
Таким образом, из приведённого рассмотрения следует, внешнее воздействие на систему взаимодействующих частиц как целое можно описать независимыми величинами: вектором полной силы вектором вращающего момента Независимость приведённых величин видна хотя бы из того, что из равенства До сих пор мы рассматривали лишь результаты внешнего воздействия на фундаментальные характеристики системы частиц – импульс Pсист и момент импульса Lсист. Для дальнейшего анализа необходимо получить выражение для энергии внешнего воздействия на систему частиц. Чтобы упростить рассмотрение, ограничимся потенциальными внешними силами, для которых
Наша цель – конкретизировать аналитическое выражение для энергии внешнего воздействия
При сдвиге системы частиц как целого на dR, а все dri º dR, из уравнения (3.18) с учётом того, что мы имеем дело с потенциальными силами, следует: dUпост = –
Аналогично рассуждая при повороте системы частиц как целого на угол dj z вокруг оси Z, проходящей через центр инерции, все dri º [djz ri]. Поэтому из уравнения (3.18) приходим к выражению вида:
Отсюда следует, что вращающий момент
Таким образом, в потенциальном поле сил, векторные характеристики внешнего воздействия на систему частиц – полная сила
Теперь мы готовы к тому, чтобы ответить на основной вопрос данного параграфа – как выглядит закон механики для вращательного движения. Во-первых, нам удалось установить, если система частиц, имеющая выделенную ось или центр, испытывает внешнее воздействие, то результатом этого воздействия является изменение её момента импульса
Работа при вращении идёт на изменение кинетической энергии вращения K = Jw2/2. Элементарное изменение работы равно элементарному изменению энергии, т.е. dAвр = dKвр = d(Jw2/2), и тогда, продифференцировав выражение кинетической энергии вращения, уравнение (3.22) может быть представлено в виде (проделали преобразования? ):
Если учесть, что
Момент силы, действующий на тело, равен произведению момента инерции на угловое ускорение.
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 905; Нарушение авторского права страницы