
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Момент импульса частицы. Понятие момента инерции
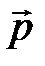 как характеристика состояния частицы обладает существенными преимуществами перед скоростью как характеристика состояния частицы обладает существенными преимуществами перед скоростью 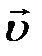 . Важнейшее из них – сохранение импульса изолированной системы . Важнейшее из них – сохранение импульса изолированной системы 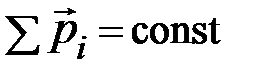 – тесно связано со свойствами пространства. Это является прямым следствием неизменности свойств изолированной системы относительно выбора начала отсчёта; другими словами, является следствием однородности пространства. Это обстоятельство наводит нас на мысль, при выборе фундаментальных характеристик состояния частицы (в мире событий) главным критерием должно служить требование сохранения этих величин для изолированной системы. Так появилась следующая фундаментальная характеристика частицы – энергия. Она, как и импульс частицы, обладает свойством аддитивности (сложения) и сохранения для изолированной системы. Эти свойства обозначенных величин, являющихся характеристиками состояния частицы, обусловлены тем, что они отражают фундаментальное свойство пространства и времени – их однородность. Рассуждая по аналогии, было бы естественно допустить, что свойства изолированной системы не должны зависеть и от выбора направлений осей координат системы отсчёта; так проявляется ещё одно свойство пространства – его изотропность; независимость характеристик состояния частицы, в нашем случае механических, от направления осей координат системы отсчёта. Иными словами, должна существовать ещё одна фундаментальная характеристика состояния частицы, проявляющая свойства аддитивности и сохранения её величины для изолированной системы, но «чувствительная» к требованию её инвариантности (неизменности) относительно поворотов системы отсчёта в пространстве. И такой характеристикой является момент импульса частицы. Почему? Специфический характер рассматриваемой величины проявляется особенно в тех случаях, когда система в целом обладает выделенной осью или центром. – тесно связано со свойствами пространства. Это является прямым следствием неизменности свойств изолированной системы относительно выбора начала отсчёта; другими словами, является следствием однородности пространства. Это обстоятельство наводит нас на мысль, при выборе фундаментальных характеристик состояния частицы (в мире событий) главным критерием должно служить требование сохранения этих величин для изолированной системы. Так появилась следующая фундаментальная характеристика частицы – энергия. Она, как и импульс частицы, обладает свойством аддитивности (сложения) и сохранения для изолированной системы. Эти свойства обозначенных величин, являющихся характеристиками состояния частицы, обусловлены тем, что они отражают фундаментальное свойство пространства и времени – их однородность. Рассуждая по аналогии, было бы естественно допустить, что свойства изолированной системы не должны зависеть и от выбора направлений осей координат системы отсчёта; так проявляется ещё одно свойство пространства – его изотропность; независимость характеристик состояния частицы, в нашем случае механических, от направления осей координат системы отсчёта. Иными словами, должна существовать ещё одна фундаментальная характеристика состояния частицы, проявляющая свойства аддитивности и сохранения её величины для изолированной системы, но «чувствительная» к требованию её инвариантности (неизменности) относительно поворотов системы отсчёта в пространстве. И такой характеристикой является момент импульса частицы. Почему? Специфический характер рассматриваемой величины проявляется особенно в тех случаях, когда система в целом обладает выделенной осью или центром. Попробуем убедиться в этом. Пусть частица массы m, обладающая импульсом
здесь Следует заметить, для свободной частицы момент импульса не является самостоятельной характеристикой, поскольку его сохранение следует непосредственно из закона сохранения импульса. Убедимся в этом. Для этого продифференцируем выражение (3.1); (зачем нужна такая математическая операция? ) В результате дифференцирования получаем выражение вида:
Здесь второе слагаемое правой части равно нулю; действительно, производная от постоянной величины Однако специфический характер рассматриваемой величины отчётливо проявляется лишь для системы частиц. Равномерное движение по окружности (рис. 3.1.) представляет собой движение в плоскости. Однако в работе [3, с. 13] мы показали, несмотря на то, что движение плоское, его можно трактовать как одномерное движение с характеристиками состояния частицы – угол поворота
Поскольку здесь sina равен единице (почему? ) (рис. 3.1.), а при движении по окружности
Из приведённых рассуждений следует: при равномерном движении по окружности, w = const, момент импульса частицы сохраняется по модулю, L = const, и имеет всего одну отличную от нуля компоненту. Направление вектора В аналитическом выражении (3.2) масса m – внутренне присущее частице число (см. с. 17), а R – радиус её удалённости от выделенной оси движения. Естественно ожидать, что произведение Итак, мы убедились в том, что при наличии выделенной оси или центра вращения характеристиками состояния частицы целесообразно выбирать такие величины, которые явно учитывают наличие элементов симметрии. В заключение параграфа сравним теперь в качестве характеристик состояния частицы угловую скорость w и момент импульса
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 813; Нарушение авторского права страницы