Неинерциальные системы отсчёта. Сила инерции
Во всех предыдущих параграфах мы рассматривали движение частицы только в инерциальных системах отсчёта (ИСО). Однако достаточно серьёзных препятствий к использованию в этих целях неинерциальных систем отсчёта (НСО) не существует. Более того, в ряде практических случаев, например, вращение планеты Земля, такие системы отсчёта обладают даже определёнными преимуществами. В своих рассуждениях ограничимся достаточно простыми типами движения НСО. Тогда оказывается, что всё различие в описании движения частицы в ИСО и НСО может быть сведено к учёту своеобразных дополнительных внешних воздействий на частицу.
Ранее отмечалось, за систему отсчёта можно выбрать любой материальный объект, к которому применима модель абсолютно твёрдого тела (а. т. т.). Напомним так же, система отсчёта является неинерциальной, если она движется с ускорением 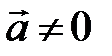 . Ограничимся рассмотрением НСО, движущейся с малыми скоростями, значительно меньшими, чем скорость света. В этом случае пространственно-временные отношения в разных системах отсчёта приближённо описываются преобразованиями Галилея, основанными на очевидных геометрических соображениях:
. Ограничимся рассмотрением НСО, движущейся с малыми скоростями, значительно меньшими, чем скорость света. В этом случае пространственно-временные отношения в разных системах отсчёта приближённо описываются преобразованиями Галилея, основанными на очевидных геометрических соображениях: 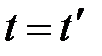 ,
, 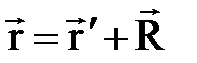 , где
, где 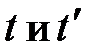 – моменты времени, а
– моменты времени, а 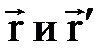 – радиус-векторы частицы в системах
– радиус-векторы частицы в системах 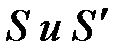 соответственно (см. рис. 1.8),
соответственно (см. рис. 1.8), 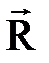 – радиус-вектор начала отсчёта
– радиус-вектор начала отсчёта 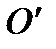 системы
системы 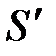 в системе отсчёта
в системе отсчёта 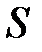 (рис. 1.8).
(рис. 1.8).
Для простоты сначала рассмотрим НСО 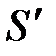 , движущуюся поступательно относительно исходной ИСО
, движущуюся поступательно относительно исходной ИСО 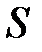 . Тогда, продифференцировав радиус-вектор
. Тогда, продифференцировав радиус-вектор 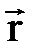 по общему времени
по общему времени 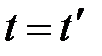 , получим выражение для скорости частицы по отношению к ИСО
, получим выражение для скорости частицы по отношению к ИСО 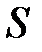 :
: 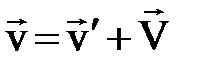 , или
, или
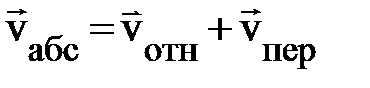 , (1.7)
, (1.7)
где по традиции скорость частицы по отношению к инерциальной системе отсчёта (ИСО) называют абсолютной ( 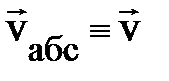 ), её скорость по отношению к НСО называют относительной
), её скорость по отношению к НСО называют относительной 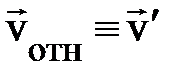 , а скорость поступательного движения неинерциальной системы отсчёта
, а скорость поступательного движения неинерциальной системы отсчёта  или скорость её начала отсчёта
или скорость её начала отсчёта 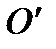 (рис. 1.8) по отношению к ИСО называют переносной (
(рис. 1.8) по отношению к ИСО называют переносной ( 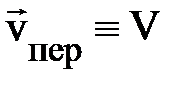 ).
).
 Рис. 1.8. Движение неинерциальной системы
отсчёта
Рис. 1.8. Движение неинерциальной системы
отсчёта  в инерциальной
системе отсчёта в инерциальной
системе отсчёта  . .
|
Дифференцируя уравнение (1.7) повторно получаем аналогичные соотношения и для соответствующих ускорений:
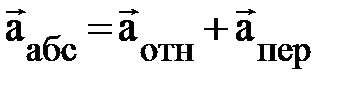 , (1.8)
, (1.8)
где, в свою очередь, 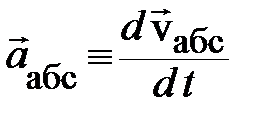 ,
, 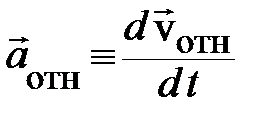 ,
, 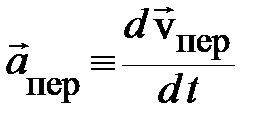 . Следует подчеркнуть ещё раз всю условность названия «абсолютная» скорость в выражении (1.7). Оно имеет смысл только для двух выбранных систем отсчёта. При переходе в любую другую ИСО аналитическое выражение для абсолютной скорости может измениться, в том числе и обратиться в нуль. Разумеется, в соответствии с законом преобразования скоростей Галилея. Заметим так же, что переносное движение частицы с
. Следует подчеркнуть ещё раз всю условность названия «абсолютная» скорость в выражении (1.7). Оно имеет смысл только для двух выбранных систем отсчёта. При переходе в любую другую ИСО аналитическое выражение для абсолютной скорости может измениться, в том числе и обратиться в нуль. Разумеется, в соответствии с законом преобразования скоростей Галилея. Заметим так же, что переносное движение частицы с 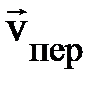 называется так только потому, что это движение неподвижной в неинерциальной системе отсчёта частицы вместе с неинерциальной системой отсчёта относительно инерциальной системы отсчёта.
называется так только потому, что это движение неподвижной в неинерциальной системе отсчёта частицы вместе с неинерциальной системой отсчёта относительно инерциальной системы отсчёта.
Наша цель – научиться описывать относительное движение частицы в НСО, считая её переносное движение заданным. При этом мы можем опираться на известные законы движения частицы в инерциальных системах отсчёта (ИСО). В принятых нами ограничениях (малые скорости движения НСО), уравнение для «абсолютного» движения частицы – это уравнение Ньютона:
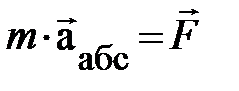 , (1.9)
, (1.9)
где 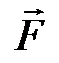 – результирующая сила, определяемая внешним окружением. В такой форме оно справедливо для любой инерциальной системы отсчёта (ИСО). Преобразуя левую часть уравнения Ньютона с помощью выражения (1.8), представим его в виде уравнения для интересующего нас относительного движения:
– результирующая сила, определяемая внешним окружением. В такой форме оно справедливо для любой инерциальной системы отсчёта (ИСО). Преобразуя левую часть уравнения Ньютона с помощью выражения (1.8), представим его в виде уравнения для интересующего нас относительного движения:
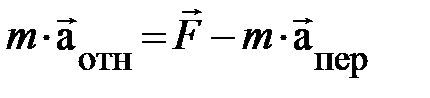 . (1.10)
. (1.10)
Это уравнение относительного движения частицы в неинерциальной системе отсчёта (НСО), движущейся поступательно. Сравним теперь два уравнения движения одной и той же частицы в ИСО и НСО соответственно. В уравнении Ньютона ускорение частицы в ИСО определяется единственной причиной. В частности, воздействием внешнего окружения, которое в модели несвободной частицы описывается результирующей силой 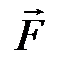 . В то же время, в уравнении (1.9) ускорение частицы в НСО определяется двумя качественно различными причинами – воздействием внешнего окружения, характеризуемым силой
. В то же время, в уравнении (1.9) ускорение частицы в НСО определяется двумя качественно различными причинами – воздействием внешнего окружения, характеризуемым силой 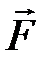 , и воздействием неравномерного движения НСО, характеризуемым переносным ускорением
, и воздействием неравномерного движения НСО, характеризуемым переносным ускорением 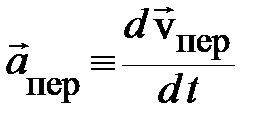 . Даже если
. Даже если 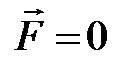 частица в НСО движется с ускорением:
частица в НСО движется с ускорением: 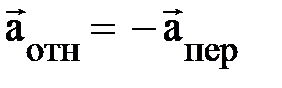 . Если же
. Если же 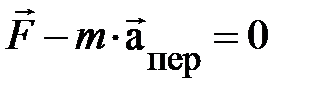 , то действие обеих причин компенсируется. В этом случае
, то действие обеих причин компенсируется. В этом случае 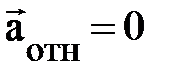 , частица в НСО движется равномерно и прямолинейно; или покоится.
, частица в НСО движется равномерно и прямолинейно; или покоится.
В заключение заметим, для нахождения закона движения частицы 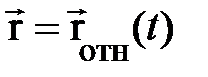 в неинерциальной системе отсчёта существенно лишь задание явного вида правой части уравнения движения (1.10). Поэтому для независимого второго члена справа в (1.10) удобно ввести обозначение
в неинерциальной системе отсчёта существенно лишь задание явного вида правой части уравнения движения (1.10). Поэтому для независимого второго члена справа в (1.10) удобно ввести обозначение 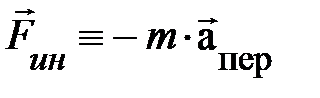 . Эту величину принято называть силой инерции (по-видимому, по причине её пропорциональности массе) или псевдосилой. Название
. Эту величину принято называть силой инерции (по-видимому, по причине её пропорциональности массе) или псевдосилой. Название 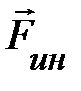 псевдосилой не в последнюю очередь обусловлено тем, что её появление не связано с воздействием окружающих материальных объектов на частицу, а определяется только характером движения НСО. Таким образом, введение силы инерции
псевдосилой не в последнюю очередь обусловлено тем, что её появление не связано с воздействием окружающих материальных объектов на частицу, а определяется только характером движения НСО. Таким образом, введение силы инерции 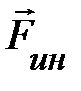 – просто способ учёта вполне реального дополнительного воздействия на частицу, связанного с переходом из ИСО в НСО. Реальность подобных воздействий читателю хорошо известна в проходе автобуса, или другого средства перемещения при торможении или разгоне.
– просто способ учёта вполне реального дополнительного воздействия на частицу, связанного с переходом из ИСО в НСО. Реальность подобных воздействий читателю хорошо известна в проходе автобуса, или другого средства перемещения при торможении или разгоне.
Не меньший интерес представляют вращающиеся системы отсчёта. Для упрощения будем считать, что угловая скорость вращения системы отсчёта 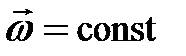 .Взаимосвязь векторов скорости частицы в ИСО и НСО остаётся без изменения(1.7):
.Взаимосвязь векторов скорости частицы в ИСО и НСО остаётся без изменения(1.7): 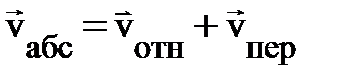 .Пусть частица движется равномерно со скоростью
.Пусть частица движется равномерно со скоростью 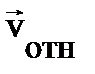 по краю равномерно вращающегося диска в направлении его вращения (рис. 1.9). Если учесть, что
по краю равномерно вращающегося диска в направлении его вращения (рис. 1.9). Если учесть, что 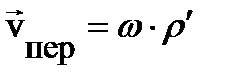 , где
, где 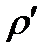 – радиус диска, из (1.7) следует
– радиус диска, из (1.7) следует 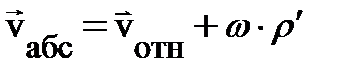 . Поскольку
. Поскольку 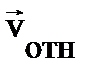 ,
, 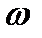 , и
, и 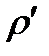 – постоянные, движение частицы в ИСО – это равномерное движение по окружности с
– постоянные, движение частицы в ИСО – это равномерное движение по окружности с 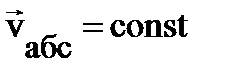 . Тогда ускорение в ИСО – это центростремительное ускорение, связанное только с изменением направления скорости
. Тогда ускорение в ИСО – это центростремительное ускорение, связанное только с изменением направления скорости 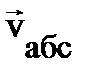 , и может быть представлено:
, и может быть представлено: 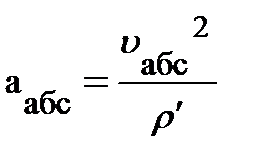 .
.
 Рис. 1.9. Вращающаяся система отсчёта
Рис. 1.9. Вращающаяся система отсчёта
|
Подставляя в правую часть полученного выражения для
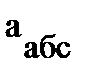
, правую часть уравнения для
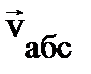
, получаем выражение вида:
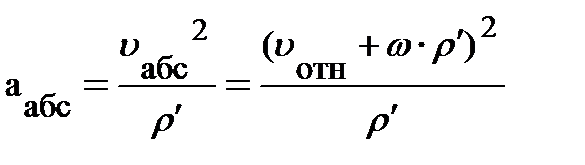
. Наконец, возводя в квадрат числитель, приходим к уравнению для абсолютного ускорения в виде:
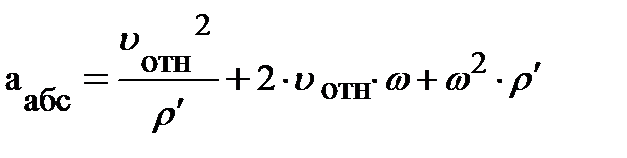
. Первый член справа – это центростремительное ускорение
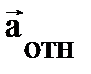
в НСО, характеризующее относительное движение частицы; следующая часть абсолютного ускорение
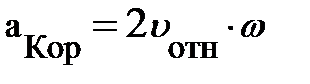
называется ускорением Кориолиса, а последнее ускорение, являясь переносным, равно
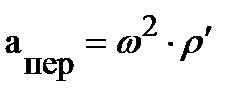
. Таким образом, последние два члена в уравнении абсолютного ускорения учитывают движение в НСО.
Воздействие вращения НСО на относительное движение частицы можно описать компактно, вновь введя соответствующие псевдосилы или силы инерции. Эти псевдосилы имеют вид 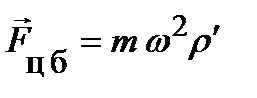 ,
, 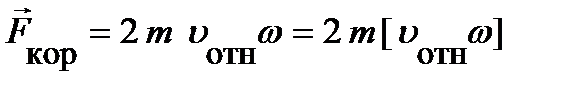 и называются, соответственно, центробежной силой инерции и кориолисовой силой. Произведение в квадратных скобках называется векторным. Его можно уточнить через концептуальный аппарат математики. Формально указанные силы можно рассматривать в качестве дополнительных сил, косвенно учитывающих внешнее воздействие, связанное с вращением НСО.
и называются, соответственно, центробежной силой инерции и кориолисовой силой. Произведение в квадратных скобках называется векторным. Его можно уточнить через концептуальный аппарат математики. Формально указанные силы можно рассматривать в качестве дополнительных сил, косвенно учитывающих внешнее воздействие, связанное с вращением НСО.
Такой подход позволяет эти дополнительные силы классифицировать стандартным образом. В частности, центробежная сила, направленная от оси вращения, является осесимметричной и потенциальной и напоминает упругую силу. Сила Кориолиса, в свою очередь, типичная гироскопическая, или прецессионная сила. Она всегда перпендикулярна относительной скорости частицы (и этим напоминает магнитную часть силы Лоренца).
Типичным примером вращающейся НСО является поверхность Земли.
Популярное:


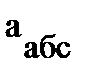 , правую часть уравнения для
, правую часть уравнения для 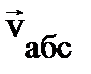 , получаем выражение вида:
, получаем выражение вида: 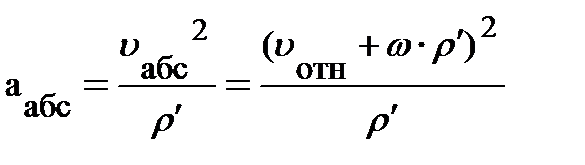 . Наконец, возводя в квадрат числитель, приходим к уравнению для абсолютного ускорения в виде:
. Наконец, возводя в квадрат числитель, приходим к уравнению для абсолютного ускорения в виде: 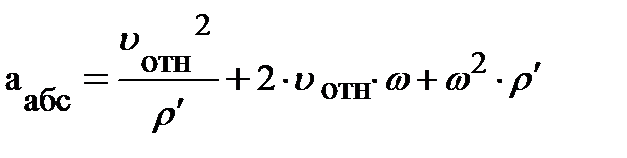 . Первый член справа – это центростремительное ускорение
. Первый член справа – это центростремительное ускорение 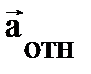 в НСО, характеризующее относительное движение частицы; следующая часть абсолютного ускорение
в НСО, характеризующее относительное движение частицы; следующая часть абсолютного ускорение 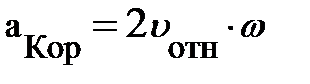 называется ускорением Кориолиса, а последнее ускорение, являясь переносным, равно
называется ускорением Кориолиса, а последнее ускорение, являясь переносным, равно 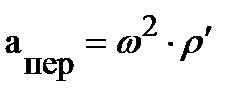 . Таким образом, последние два члена в уравнении абсолютного ускорения учитывают движение в НСО.
. Таким образом, последние два члена в уравнении абсолютного ускорения учитывают движение в НСО.