Релятивистский импульс и релятивистская энергия

⇐ ПредыдущаяСтр 12 из 23Следующая ⇒

Ранее, с. 15–17, мы убедились в том, что понятие импульса как характеристика состояния частицы обладает существенными преимуществами перед скоростью. Во-первых, через массу понятие отражает специфику материальных объектов, моделируемых частицами, которая проявляется при их взаимодействии. Во-вторых, импульс, в отличие от скорости, для систем свободных частиц аддитивен. В-третьих, для изолированных систем импульс, в отличие от скорости, сохраняется, и это свойство не зависит от выбора медленно u < < с движущихся ИСО. В-четвёртых, понятие импульса универсально. В частности, независимая процедура для определения массы света отсутствует. Тем не менее, импульс света можно определить, например, по двухчастичному распаду, если вторым продуктом распада является частица массы М. Примером такого распада может служить процесс излучения света первоначально покоящимся атомом. Учитывая, что атом до испускания света и атом вместе со светом после его испускания образуют изолированную систему, естественно было бы предположить, что импульс системы первоначально равный нулю, сохраняется. Тогда можно считать, что импульс света 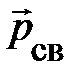– векторная величина, определяемая условием: 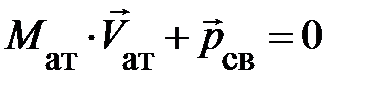. Измеряя на опыте скорость движения атома после излучения и, зная его массу , которую можно считать неизменной, можем определить импульс света. Отсюда следует, импульс – универсальная характеристика любых материальных объектов, имеющая смысл целостной фундаментальной величины, не зависящей в общем случае от массы и скорости.

Это обстоятельство позволяет предположить, что импульс может сохранить смысл характеристики состояния и при больших скоростях движения. По крайней мере, это верно для света, ибо между его импульсом и скоростью нет жёсткой связи. По-видимому, такими же качествами должен обладать импульс любой частицы с m ¹ 0 при её движении с предельной скоростью, близкой к скорости света.

Возникает, однако, вопрос, сгодится ли для этой цели конкретное выражение для нерелятивистского импульса частицы 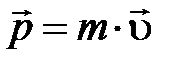, полученное при малых скоростях. Многочисленные эксперименты [2] с распадами и столкновениями элементарных частиц, движущихся с околосветными скоростями, показали, что установленные выше свойства импульса и массы в этих условиях не выполняются: нерелятивистский импульс системы частиц не сохраняется; масса системы величина неаддитивная; суммы масс начальных и конечных частиц, как правило, не совпадают: 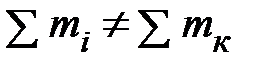. Таким образом, несмотря на то, что выбор импульса вместо скорости в качестве характеристики состояния частицы явно предпочтителен, конкретное выражение для нерелятивистского импульса оказывается непригодным, так что его обобщение неизбежно.

Важнейшим преимуществом импульса как характеристики состояния частицы перед скоростью является его сохранение в изолированной системе и тесно связанное со свойствами пространства. Приступая к обобщению понятия импульса частицы, мы должны стремиться к тому, чтобы оно стало пригодным для описания экспериментов при любых скоростях.

В определение нерелятивистского импульса 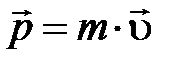входят две величины: специфическая характеристика частицы – масса m и пространственно-временная характеристика – скорость u. Масса m служит неизменной «визитной карточкой» внутренне присущей частице при любых скоростях. Вследствие её определения через измерение в пределах u ®0 она не зависит от скорости частицы. Поэтому естественно предположить, что определённая таким образом масса – это не только скаляр, но и инвариант, не зависящий от выбора любых ИСО.

Формулы преобразований Лоренца для проекций вектора скорости при переходе в различные ИСО сложны, см. (4.14), что предопределяет неинвариантный характер произведения mu_х = m× dx/dt. В то же время мы знаем, что помимо неинвариантной величины dt существует инвариантное (4.17) собственное время 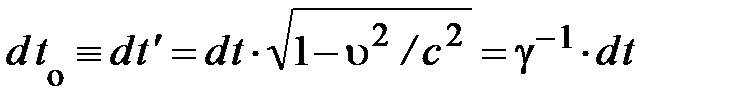. Таким образом, хотя вектор 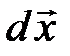сам по себе нековариантен, его можно трактовать как совокупность пространственных проекций ковариантной величины пространственно-временного интервала 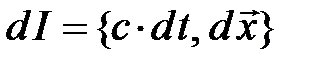: 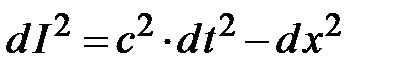; для простоты записи (4.15) здесь используются преобразования Лоренца на плоскости X t. Таким образом, естественным обобщением нерелятивистского импульса частицы служит величина

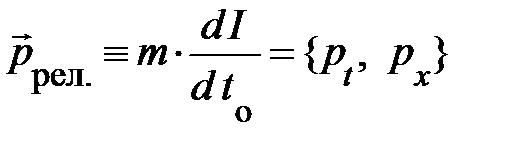. (4.18)

Поскольку величина 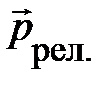образована из двух инвариантов m и 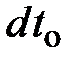и интервала dI, при преобразованиях Лоренца она преобразуется как пространственно-временной интервал, так что выражение (4.18) одинаково во всех ИСО. Чтобы выяснить физический смысл 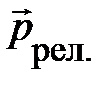, рассмотрим его проекци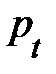и и 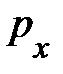по отдельности.

Прежде всего, пространственная проекция 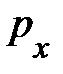образует вектор на плоскости X t:

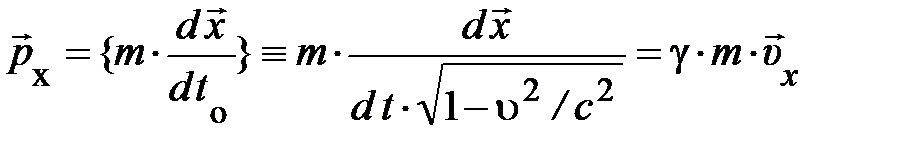. (4.19)

Нетрудно убедиться, что этот вектор в пределе u < < с переходит в нерелятивистский импульс 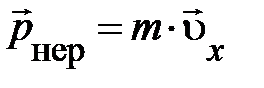. Поэтому его (4.19) принято называть релятивистским импульсом, иначе импульсом частицы.

Сравним теперь поведение релятивистского импульса и скорости частицы при больших значениях последней (u ~ с). В этом пределе u » с = = const, а модуль релятивистского импульса 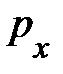неограниченно возрастает. Таким образом, обобщение нерелятивистского импульса привело к величине вида (4.19), которая совместно с радиус-вектором частицы на плоскости X t фиксирует в общем случае её состояние в момент времени t при любых скоростях и в любой ИСО.

Здесь важно подчеркнуть, что при обобщении от нерелятивистского вектора 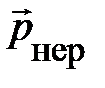к релятивистскому 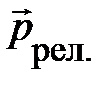импульсу меняется не только сам вектор 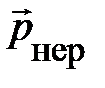. Вектор 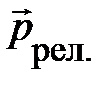как единая величина во всех ИСО содержит ещё одну проекцию-скаляр (4.18):

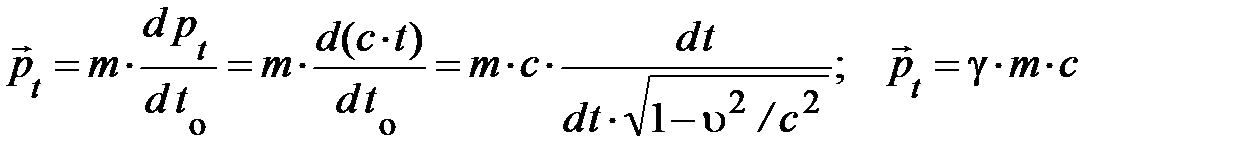. (4.20)

Исторически сложилось так [2], что принято иметь дело не с самой 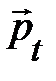, а с величиной:

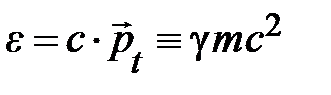, (4.21)

называемой релятивистской энергией частицы или её полной энергией. По сути, релятивистская энергия e (4.21) вместе с её релятивистским импульсом 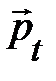(4.20) – проекции единой ковариантной величины 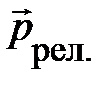(4.18) – вектора энергии-импульса, представленного для плоскости X t. Естественно, при переходе от одной ИСО к другой они преобразуются согласно формулам, следующим из преобразований Лоренца. В частности, при переходе в ИСО, движущуюся вдоль оси Х, для 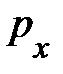и e справедливы преобразования, аналогичные преобразованиям Лоренца (4.13), (4.14):

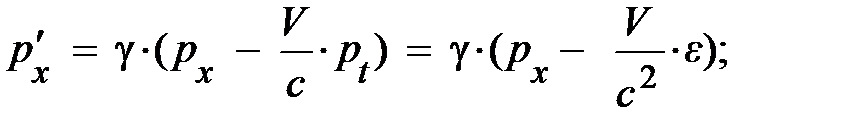
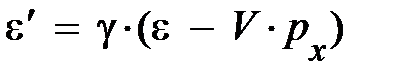. (4.22)

Для свободной частицы, согласно закону инерции, скорость 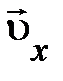= = const, так что её вектор импульса (4.18) также постоянен 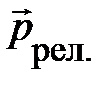= const. Для отдельных его проекций (4.19) и (4.21) выражения примут вид:

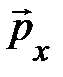= const, e = const, (4.23)

что означает, релятивистский импульс 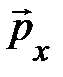и релятивистская энергия e свободной частицы сохраняются. Однако следует заметить, релятивистский импульс частицы 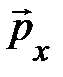сохраняется во всех ИСО только при условии, что одновременно сохраняется и её релятивистская энергия, и наоборот. Таким образом, сделанное выше обобщение понятия нерелятивистского импульса частицы справедливо и для других изолированных систем. Как показывают многочисленные эксперименты [2], оно приводит вместо (4.23) к законам сохранения импульса 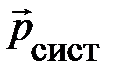и энергии 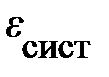для изолированных систем, отражающим фундаментальные свойства однородности пространства и времени, и свойствам их аддитивности для системы свободных частиц. Причём эти свойства аналогичны свойствам, которыми обладал нерелятивистский импульс при малых скоростях. Кроме того, в нерелятивистском пределе u < < с, когда 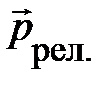® 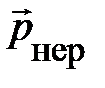, энергия частицы (4.21) не исчезает: e ® 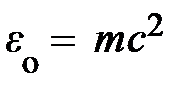. Тем самым свойства сохранения и аддитивности энергии, справедливые при любых скоростях, переходят в этом пределе в известные свойства сохранения и аддитивности массы, справедливые лишь при малых скоростях.

Итак, преобразования Лоренца для проекций импульса и энергии (4.22) справедливы во всех ИСО. На опыте же удобны две ИСО – лабораторная система (ЛСО) S, в которой находится наблюдатель, и собственная или сопровождающая система (ССО) , в которой покоится частица. В этой системе 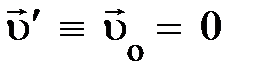, а V = u, так что:

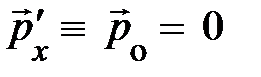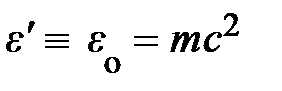; . (4.24)

То, что импульс покоя частицы оказался равным нулю, естественно. В то же время энергия покоя частицы 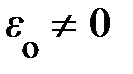. Поскольку она выражается через инварианты m и c, энергия покоя 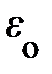сама является инвариантом, т.е. характеристикой, внутренне присущей частице. Сравнение формул (4.19) – – (4.21) и (4.24) показывает, что выражения для импульса и энергии можно привести к виду, более удобному для обобщения:

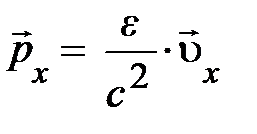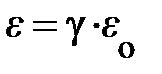; . (4.25)

Первая формула даёт определение скорости частицы 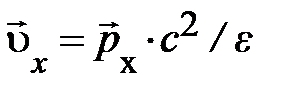через фундаментальные величины – проекции вектора 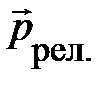(4.18) – импульс 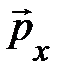и энергию 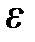. Вторая формула (4.25) связывает энергию 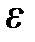с инвариантом 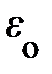соотношением, эквивалентным формуле (4.6), выражающей промежуток времени d t через инвариантное собственное временя .

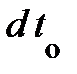Вспомним, важнейшей характеристикой всякого четыревектора, является квадрат его модуля (4.15). В нашем случае для плоскости X t (4.18) с учётом (4.21) и (4.24) примет вид: 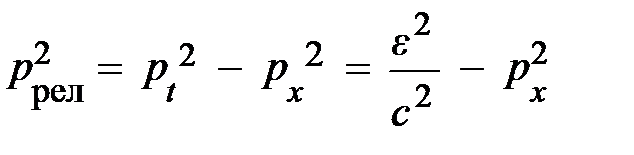. Квадрат четыревектора энергии-импульса, в силу одинаковости его величины во всех ИСО, для ССО запишется:

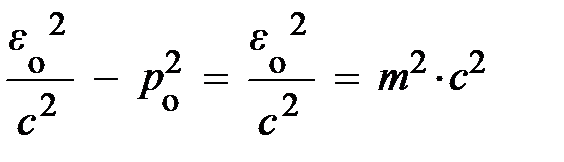. (4.26)

Это значит, что масса частицы, инвариантность которой в мире событий устанавливается независимо на опыте, инвариантна вовсе не случайно. Она обладает новым фундаментальным качеством – служить «квадратом длины» четыревектора (4.18), связывающим воедино в любой ИСО две важнейшие характеристики частицы – релятивистскую энергию e и релятивистский импульс 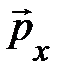. И тогда из (4.26) следует, связь между энергией e, модулем p и массой m, справедливая в любой ИСО, запишется:

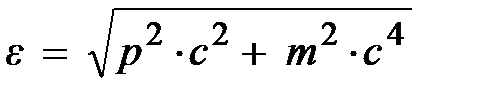. (4.27)

Таким образом, заслуга Эйнштейна состоит в установлении нового свойства массы. В связи с этим формула (4.27) называется формулой Эйнштейна. Обычно её записывают в виде 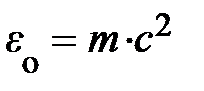и говорят, что она выражает эквивалентность массы и энергии покоя. Однако, по мнению А.Д. Суханова [2], это высказывание очень неточно передаёт суть дела. Как утверждает автор, речь должна идти о наличии у одной и той же величины (массы) двух независимых и качественно различных свойств –быть мерой инертности и определять «квадрат длины» четыревектора энергии-импульса в мире событий по измеряемым независимо энергии e и импульса .

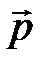Из определения релятивистской энергии частицы (4.25) или (4.27) следует, что она скаляр в трёхмерном пространстве и не является инвариантом в мире событий, т.е. её значение зависит от выбора ИСО. В произвольной ИСО релятивистскую энергию e всегда можно представить в виде суммы инварианта – энергии покоя 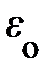и кинетической энергии К, зависящей от скорости частицы в данной ИСО, т.е. e = 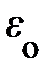+ К, где 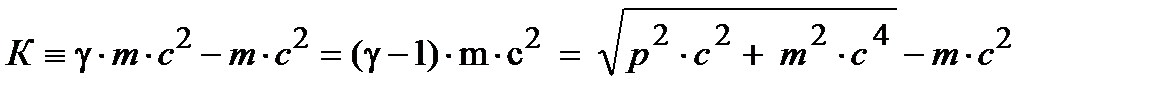по определению.

Учитывая важную роль импульса частицы, целесообразно выразить его модуль через кинетическую энергию: .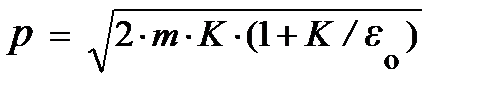

Колебательное движение

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒