
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Относительность длины отрезка
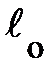 и неподвижной и неподвижной 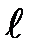 инерциальных систем отсчёта (ИСО) обратимся к рис. 4.3. Система S / движется со скоростью V направо вдоль оси х системы S. Установление соотношения длин отрезков требует выполнения математической операции деления, например, длины l в неподвижной системе отсчёта S на длину lо в движущейся системе отсчёта S /, т.е. l / lо. инерциальных систем отсчёта (ИСО) обратимся к рис. 4.3. Система S / движется со скоростью V направо вдоль оси х системы S. Установление соотношения длин отрезков требует выполнения математической операции деления, например, длины l в неподвижной системе отсчёта S на длину lо в движущейся системе отсчёта S /, т.е. l / lо.
Для определения длины отрезка (l, или lо), как правило, привлекается процесс сравнения с эталоном длины. Такую процедуру в нашем повседневном опыте нам приходится выполнять регулярно. Однако заметим, эталон единицы длины у нас определён; это система интернациональная СИ, в которой единица длины метр, и внесистемные единицы. Здесь сложение; неинвариантность понятия одновременности удалённых событий в произвольно движущихся ИСО (см. (4.6)), и принцип существования предельной скорости указывают на то, что единица длины в каждой из систем отсчёта должна определяться скоростью света с и временным интервалом соответствующей ИСО. Отсюда немедленно следует, интервал единица длины в ИСО S / Dlо = с× t /, а в инерциальной системе отсчёта S Dl = с× t. И тогда длина отрезка в движущейся системе отсчёта l / = lо/Dlо = = lо/с× t /, а в неподвижной S системе l = lо/Dl = lо/с× t. Отсюда соотношение длин отрезков запишется: l / l / Учитывая формулу (4.6), длина тела l, измеренная в неподвижной ИСО в направлении её движения, запишется:
где l / – длина отрезка в подвижной системе отсчёта. Иначе говоря, длина отрезка (тела), измеренная в движущейся ИСО в направлении её движения l /, испытывает сокращение. Максимальной длиной тело обладает в системе отсчёта, в которой оно покоится. Сделанный вывод относится к размерам тела лишь в направлении движения ИСО. В поперечном направлении размеры тела не изменяются, так что, например, объём куба при измерении в движущейся инерциальной системе отсчёта изменяется по закону
здесь под корнем отношение V2/с2 заменено постоянной b – бета, что упрощает запись и чаще встречается в литературе. В заключение следует подчеркнуть, описанные выше эффекты не связаны с действием каких-либо сил. Они отражают лишь неинвариантность понятий промежутка времени и длины в мире событий.
4.5. Преобразования Лоренца Завершая анализ свойств пространства и времени, будем исходить из твёрдо установленных на опыте фундаментальных принципов. Из них, в частности, следует, процедура синхронизации часов в произвольной инерциальной системе отсчёта (ИСО) может осуществляться светом, и при этом с > V, но необязательно с > > V.
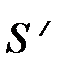 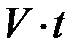 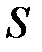 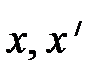 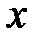 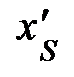 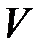 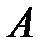 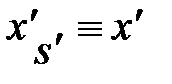 Снова обратимся к случаю, когда система S / движется со скоростью V направо вдоль оси Х системы S (рис. 4.4). Координата события в • А Снова обратимся к случаю, когда система S / движется со скоростью V направо вдоль оси Х системы S (рис. 4.4). Координата события в • А 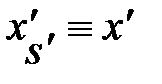 – это расстояние, измеренное от точки А до начала отсчёта движущейся ИСО S / (верхняя пунктирная линия). То же расстояние, измеренное по отношению к неподвижной системе отсчёта S, запишется (см. рис. 4.4): – это расстояние, измеренное от точки А до начала отсчёта движущейся ИСО S / (верхняя пунктирная линия). То же расстояние, измеренное по отношению к неподвижной системе отсчёта S, запишется (см. рис. 4.4):
Учитывая взаимосвязь длин отрезков в подвижной и в неподвижной системе отсчёта уравнения (4.8),
Приняв к сведению, что
. (4.12)
Поскольку левые части системы уравнений (4.12) равны, после несложных преобразований пытливый читатель получает уравнение, отражающее взаимосвязь координат в движущейся (S / ) и неподвижной (S) инерциальных систем отсчёта (ИСО):
Убедились? Теперь перейдём к получению взаимосвязи моментов времени произвольного события. Из формулы (4.6) время в движущейся системе отсчёта
Такого рода соотношения (4.13) и (4.14) называются преобразованиями Лоренца. Впервые они были выполнены Лоренцем. Он обратил внимание на то, что после таких преобразований форма уравнений Максвелла в теории электромагнетизма не изменяется. Для Эйнштейна этот факт оказался решающим аргументом при формулировке принципа относительности и существования предельной скорости движения материальных объектов. 4.6. Пространственно-временной интервал Из преобразований Лоренца (4.13) и (4.14) следует, расстояние Dr и промежуток времени Dt сами по себе не пригодны для объективного описания пространственно-временных отношений между событиями в совокупности произвольно движущихся ИСО. Задача состоит в том, чтобы найти комбинацию из неинвариантных по отдельности величин Dr и Dt, которая не изменялась бы относительно всех ИСО. Решая её, следует исходить лишь из твёрдо установленного факта неизменности скорости света в любых двух ИСО. А именно, рассмотрим относительно систем S и S / два специфических события – испускание светового сигнала и последующий его приём. Из равенства с / = с следует, что для таких событий с / = Dr / /Dt / = Dr/Dt = с. Это значит, что определённая комбинация из расстояния Dr и промежутка времени Dt с2× (Dt / )2 – (Dr / )2 = с2× (Dt)2 – (Dr)2 = 0 остаётся здесь неизменной, хотя сами по себе расстояние (Dr ¹ Dr / ) и промежуток времени (Dt ¹ Dt / ) могут изменяться. Переходя к рассмотрению пары произвольных событий, введём для них, по аналогии с приведённым примером, новую величину DI, называемую пространственно-временным интервалом между событиями или просто интервалом. По определению квадрат интервала запишется: DI 2 = с2× Dt2 – Dr2 = с2× Dt2 – Dx2 – Dy2 – Dz2. (4.15) Если в предыдущем примере он был равен нулю, то для произвольных событий он отличен от нуля. Однако, согласно преобразованиям Лоренца (4.13), (4.14) остаётся инвариантом, неизменным в любой ИСО: DI / º DI. (4.16) Убедимся в этом. В системе S / Dt / = g× Тогда, с учётом (4.13) DI / 2 = с2× Dt / 2 – Dx / 2 – Dy / 2 – Dz / 2 = = c2× g2× = c2× g2× В последнем равенстве после раскрытия квадратных скобок слагаемые, с удвоенным произведением, сокращаются. Объединив члены с Dt2 и Dx2, получаем DI / 2 = Dt2× g2× (с2 – V2) – Dx2× g2× (1 – V2/с2) – Dy2 – Dz2 = с2× Dt2 – Dx2 – Dy2 – Dz2 = DI 2, Здесь пытливый читатель должен увидеть, что произведение скобок с g2 ведёт к 1. Проведённые преобразования позволяют утверждать, что именно интервал DI, а не расстояние Dr и промежуток времени Dt по отдельности следует считать объективной характеристикой пространственно-временных отношений. Таким образом, «переворот, произведённый Эйнштейном во взглядах на пространство и время, вовсе не сводится к установлению взаимосвязей пространственных и временных отношений или относительности некоторых понятий. Заслуга Эйнштейна, скорее, в том, что вместо одних «очевидно» инвариантных величин (Dr и Dt) он ввёл другие инвариантные величины (DI), более пригодные для отражения объективных свойств мира событий, установления подлинного единства пространственных и временных отношений» [2]. Убедимся в том, что понятие интервала DI богаче понятия расстояния. Расстояния в пространстве либо всегда положительны, либо равны нулю: Dr ³ 0. В то же время в мире событий кроме DI 2 < 0 – пространственноподобных интервалов, могут существовать интервалы с DI 2 > 0, называемые времениподобными и с DI 2 = 0 – светоподобными. Для пар событий, разделённых времениподобными интервалами с DI 2 > 0, вместо интервала DI можно ввести более удобное понятие – собственное время движущегося объекта. Действительно, пусть в системе S с постоянной скоростью u движется частица с массой m ¹ 0. За промежуток времени Dt она сместится на расстояние Dr = u× Dt. Интервал DI между событиями, соответствующий началу и концу её движения, в системе S равен: DI = Перейдём в ССО (собственную или сопровождающую систему отсчёта) S / = Sо, движущуюся относительно S с той же скоростью
Величину В заключение параграфа заметим, несмотря на то, что хотя промежуток времени Dt между парой одних и тех же удалённых событий с DI 2 > 0 относителен, понятия «раньше», «позже», «одновременно» для этой пары событий абсолютны. Они все, согласно (4.17), определяются инвариантной величиной
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 797; Нарушение авторского права страницы