Анализ альтернативных проектов

По степени конкуренции между собой можно выделить следующие инвестиционные проекты:

– независимые;

– альтернативные (взаимоисключающие);

– взаимодополняющие.

Все независимые проекты (инвестиции) при наличии необходимых средств могут быть реализованы, и конкурируют между собой только в случае ограничения финансовых средств. Альтернативные проекты конкурируют между собой по способу достижения одной и той же цели.

Задача данного раздела – определить критерий выбора одного или нескольких проектов из имеющихся альтернатив.

Так, при сравнительной оценке эффективности инвестиций в альтернативные проекты различают следующие ситуации:

1. Сравниваемые альтернативы имеют одинаковый срок реализации проекта. В этом случае лучший проект рекомендуется выбирать по максимуму ЧДД, поскольку установка на увеличение ценности фирмы (богатства инвестора) считается приоритетной, или по внутренней норме доходности приростных (дополнительных) инвестиций, если объем инвестиций по двум сравниваемым проектам неодинаков. При этом приростные инвестиции определяются как разница инвестиций по сравниваемым вариантам. Если ВНД приростных инвестиций больше или равна норме дисконта, то проект с большими инвестициями будет предпочтительней.

 Если норма дисконта окончательно не определена (т. е. имеется несколько ее значений), то целесообразно использовать кривые зависимости ЧДД от нормы дисконта по сравниваемым альтернативам, а затем, руководствуясь критерием максимума ЧДД, принимать решение. Точка пересечения таких кривых называется точкой Фишера. В этой точке по критерию ЧДД проекты равнозначны, а значит, для выбора лучшего при данной норме дисконта Е следует руководствоваться критерием максимума индекса доходности (если инвестиции по проектам различны).

 Например, имеется на выбор два проекта – А и Б. Следует выбрать лучший проект, если норма дисконта:

а) X%;

б) Y%.

Представленная ситуация изображена на рис. 5.1.

Как показывает рис. 5.1, при всех значениях Е › F предпочтительней вариант А, так как ЧДД_А › ЧДД_Б, при всех значениях Е ‹F предпочтительней проект Б.

2. Сравниваемые альтернативы имеют различный срок реализации проекта. Для выбора лучшего проекта используются следующие методы:

– метод цепного повтора;

– метод бесконечного цепного повтора;

– метод эквивалентного аннуитета.

Несмотря на различие результатов оценки в абсолютном выражении, использование данных методов приводит к одинаковому выбору.

 

                                      ЧДД

                                                     проект Б

                              

 

 

                      ЧДД (Х) _Б проект А                        

                                                                      

                      ЧДД (Х)^А                      

ЧДД (F)_А=ЧДД (F)_Б                            т. Фишера

                                                                   Б          А   

                             ЧДД (Y)_А

                             

                             ЧДД (Y)_Б

                             

                                       

                                                                 Х F  Y                               E.%

 

Рис. 5.1. Схема выбора инвестиционного проекта

 

Метод цепного повтора. Рассчитывается наименьший общий срок реализации проектов (как наименьшее общее кратное), ЧДД по каждому проекту, количество повторов реализации каждого проекта за наименьший общий срок и по максимуму суммарного ЧДД, учитывающего число повторений, выбирается лучший вариант инвестирования.

 Пусть срок службы проекта А – Т_А лет, Б – Т_Б лет, наименьший общий срок реализации проектов, т. е. НОК (Т_А; Т_Б) = z, тогда за период z проект А можно реализовать n_А раз = z /T_A; Б – n_Б раз (n_Б = z/T_Б). ЧДД по проектам при условии однократного осуществления составит, соответственно, ЧДД_А  и ЧДД_Б.

Для определения суммарного ЧДД по каждому проекту при условии его реализации n_раз за период z используют формулу:

 

(5.1)

                           

 

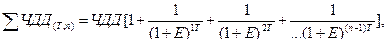
где _{(т; n )} – суммарный ЧДД по проекту со сроком жизни Т, реализуемому n раз; ЧДД – дисконтированный доход по проекту со сроком службы Т при однократной его реализации; n – число повторов, причем число слагаемых в скобках равно n.

 

Если ∑ ЧДД^А_{(Та; nа)}  превышает ∑ ЧДД^б_{(Тб; nб)}, то следует выбрать проект А, и наоборот.

Логика расчетов представлена на рис. 5.2.

                        

                                           ДП₂      ДП_Т            ДП_Т+2= ДП₂       ДП_2Т= ДП_Т

 

                                                                   ДП_Т+1= ДП₁

                                               …                                        …        …

                        

     ДП₁ О  1     2                     Т Т+1 Т+2             2Т

   (1+Е)

    ДП₂

     + (1+Е)²

                …

   ДП_Т

(1+Е)^Т

                  

     ЧДД_Т

 

 

 

                                                       n =1  ДП _Т+1

                                                   1+Е

                                                  ДП _Т+2

                                                  (1+Е)²

                                        +    …

                                                   ДП _2Т

                                                  (1+Е)^Т

                                                               

                                                   ЧДД_Т

ЧДД_Т

          (1+Е) ^1т

    …

ЧДД _{(т; n)}

Рис 5.2. Определение суммарного ЧДД

 

Поскольку условия реализации проектов иногда приводят к утомительным расчетам, прибегают к более простым методам.

Метод бесконечного цепного повтора. Если сравниваемые проекты существенно различаются по продолжительности, можно предположить, что каждый из анализируемых проектов будет реализован бесконечное число раз, то есть число слагаемых в формуле (5.1) будет стремиться к бесконечности:

(5.2)

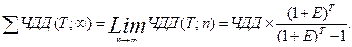
По максимуму суммарного чистого дисконтированного дохода выбирается лучший проект.

Метод эквивалентного аннуитета. Аннуитет- вид денежного потока с равными значениями по годам (интервалам планирования, шагам расчета).

Формула ЧДД в случае аннуитета примет вид:

 

ЧДД= ДП _t ДП _t  = ДП _t PV A 1_{Т; E}.               (5.3)

 

где PV A 1 _{T ; E} – текущая стоимость аннуитета суммой в 1 рубль, получаемого в конце периода t [ t? 1; T ].

Эти множители приведены в специально разработанных таблицах.

Эквивалентный аннуитет (ЕА) – аннуитет, который имеет ту же продолжительность, что и оцениваемый инвестиционный проект, и тот же чистый дисконтированный доход, что и ЧДД рассматриваемого проекта:

 

(5.4)

 

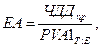
где ЧДД_пр - чистый дисконтированный доход по проекту.

 Следует отметить, что эквивалентный аннуитет (ЕА) в (5.4) полностью соответствует денежным поступлениям (ДП) в выше приведенной формуле (5.3).

Таким образом, задача сводится к нахождению годовой величины аннуитета – аналога (эквивалента) годовых денежных поступлений по проекту, которые аннуитетом не являются.

 Определив эквивалентный аннуитет (ЕА) по каждому проекту, выбирают проект с максимальным его значением, так как проект с большим эквивалентным аннуитетом будет обеспечивать и больший ЧДД при любом горизонте расчета.

Условия применения всех перечисленных методов:

1) молчаливое распространение всех исходных условий на будущее (что не всегда корректно), т. е. абстрагирование от реальности;

2) если исходным параметрам свойственна достаточная неопределенность, то можно не принимать во внимание различие в продолжительности их действия и ограничиться стандартными критериями (например, простым ЧДД).

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться: