Предел функции нескольких переменных.
При рассмотрении предела функции одной переменной 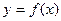 было введено понятие окрестности точек. Под окрестности точки
было введено понятие окрестности точек. Под окрестности точки 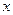 там понимался интервал, содержащий эту точку. При введении понятия предела для функции нескольких переменных мы будем рассматривать окрестность двумерной точки
там понимался интервал, содержащий эту точку. При введении понятия предела для функции нескольких переменных мы будем рассматривать окрестность двумерной точки 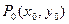 в плоскости
в плоскости  , окрестность трёхмерной точки
, окрестность трёхмерной точки 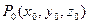 в пространстве
в пространстве 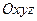 , и, вообще, окрестность n – мерной точки
, и, вообще, окрестность n – мерной точки 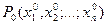 в n – мерном пространстве.
в n – мерном пространстве.
Определение. Окрестностью точки 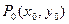 радиуса
радиуса 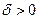 называется внутренность круга с центром в этой точке радиуса
называется внутренность круга с центром в этой точке радиуса 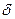 . Окрестностью точки
. Окрестностью точки 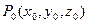 радиуса
радиуса 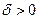 называется внутренность шара с центром в этой точке радиуса
называется внутренность шара с центром в этой точке радиуса 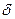 . Обозначают такую окрестность
. Обозначают такую окрестность 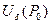 и называют
и называют 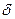 - окрестностью точки
- окрестностью точки 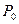 . Очевидно, что любая точка P(x,y) на плоскости, принадлежащая
. Очевидно, что любая точка P(x,y) на плоскости, принадлежащая 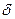 - окрестности точки
- окрестности точки 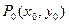 , находится от этой точки на расстоянии, меньшем
, находится от этой точки на расстоянии, меньшем 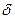 . Аналогично, любая точка
. Аналогично, любая точка 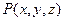 в пространстве, принадлежащая
в пространстве, принадлежащая 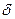 - окрестности точки
- окрестности точки 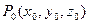 , также находится от этой точки на расстоянии, меньшем
, также находится от этой точки на расстоянии, меньшем 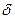 .
.
В пространстве n измерений 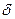 – окрестностью точки
– окрестностью точки 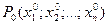 называется множество всех точек
называется множество всех точек 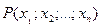 , расстояние каждой из которых от точки
, расстояние каждой из которых от точки 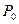 меньше
меньше 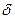 , т.е.
, т.е. 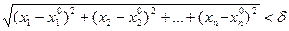 .
.
Если из 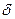 - окрестности точки
- окрестности точки 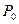 удалить саму точку
удалить саму точку 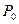 , то мы получим проколотую
, то мы получим проколотую 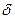 - окрестность точки
- окрестность точки 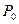 , которая обозначается
, которая обозначается 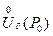 .
.
Пусть функция 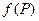 определена в окрестности
определена в окрестности 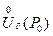 .
.
Определение. Число 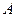 называется пределом функции двух переменных
называется пределом функции двух переменных  при
при 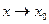 и
и 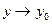 , т.е. при
, т.е. при 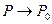 , если для любого числа
, если для любого числа 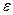 >0 найдётся такая выколотая
>0 найдётся такая выколотая 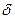 - окрестность точки
- окрестность точки 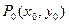 , что для любой точки
, что для любой точки 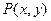 этой окрестности выполняется неравенство
этой окрестности выполняется неравенство
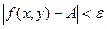
 или
или 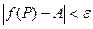 .
.
При этом пишут 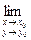
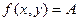 или
или 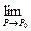
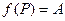 .
.
Определение предела функции через кванторы можно записать следующим образом:
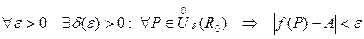 .
.
Написанное таким образом определение справедливо для функции любого числа переменных. При этом точки 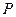 и
и 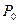 , окрестность
, окрестность 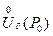 рассматриваются в пространстве соответствующей размерности.
рассматриваются в пространстве соответствующей размерности.
Заметим, что, если число 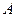 является пределом функции
является пределом функции 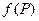 , то
, то 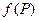 стремится к
стремится к 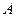 , при этом точка
, при этом точка 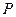 произвольным образом неограниченно приближается к точке
произвольным образом неограниченно приближается к точке 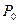 . Из этого следует, что, если при приближении точки
. Из этого следует, что, если при приближении точки 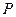 к
к 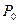 по различным направлениям функция имеет различные предельные значения, то при
по различным направлениям функция имеет различные предельные значения, то при 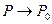 функция предела не имеет.
функция предела не имеет.
Пример 4.6. Найти предел функции 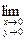
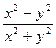 .
.
Решение. Заданная функция определена на всей плоскости за исключением начала координат. Пусть точка 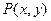 приближается к началу координат по оси
приближается к началу координат по оси 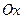 , где
, где 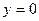 . Тогда
. Тогда 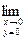
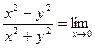
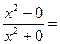 1. Если же точка
1. Если же точка 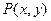 приближается к началу координат по оси
приближается к началу координат по оси 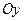 , где
, где 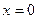 , то
, то 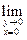
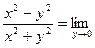
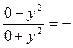 1.
1.
Мы видим, что при приближении точки 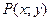 к началу координат по различным направлениям функция имеет различные предельные значения. Следовательно, предела при
к началу координат по различным направлениям функция имеет различные предельные значения. Следовательно, предела при 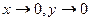 не существует.
не существует.
Функция нескольких переменных называется бесконечно малой, если её предел равен нулю. Вообще можно показать, что для функций нескольких переменных справедливы теоремы о пределах и правила нахождения пределов, рассмотренные для функции одной переменной в главе 2.
Пример 4.7. Найти 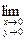
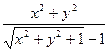 .
.
Решение. Имеем неопределённость вида 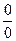 . Домножим числитель и знаменатель на выражение, сопряжённое знаменателю, получим:
. Домножим числитель и знаменатель на выражение, сопряжённое знаменателю, получим:
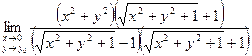
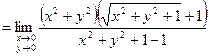 =
=
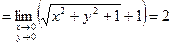 .
.

