На тему « Управление процессами» ⇐ ПредыдущаяСтр 2 из 16Следующая ⇒   Раздаточный материал   1. Управление процессами является ёмкой, универсальной категорией, которая в зависимости от цели рассмотрения и использования имеет различное толкование. Управление процессами можно рассматривать с различных позиций: социально-экономической; научно-технической, производственно – технологической, организационной, и других. В условиях глобализации управление процессами во многом определяет конкурентоспособность предприятия. 2. Вам предлагается на отдельном листе продолжить следующие три предложения: 1. «В моем представлении управление процессами – это …» 2. «Ожидаю, что в процессе изучения дисциплины …» 3. «Опасаюсь, что в ходе изучения дисциплины …» Практическое занятие № 2 На тему « Управление процессами» Раздаточный материал 1. Виды диаграмм рассеивания (разброса)         2. Интерпретация гистограмм   Рисунок 2.1 Центрированный процесс с малой вариацией Рисунок 2.2 Центрированный процесс с большой вариацией Рисунок 2.3 Нецентрированный процесс с малой вариацией Рисунок 2.4 Гистограмма с двумя пиками Рисунок 2.5 Усеченная гистограмма Практическое занятие № 3 На тему « Управление процессами»                                         Расчёт состояния процесса   Рассмотрим пример расчёта уровня sigma для процесса. Расчёт состоит из ряда шагов.  1. Выбрать процесс, который надо оценить и для которого имеются исходные данные.  2. Определить количества единиц N, участвующих в процессе.                    Пусть N = 13.  3. Определить количество нормальных, бездефектных единиц NQ.                    Пусть NQ = 11.  4. Найти отношение D = NQ / N = 11/13 = 0,846.  5. Вычислить коэффициент дефектов К = 1 – D = 0,154.  6. Определить число потенциальных участков n , где могут возникнуть дефекты. Пусть n = 24.  7. Вычислить коэффициент дефектности TQ = K / n = 0,0064.  8. Вычислить число дефектов на 1 миллион возможных QM :                           QM = TQ x 1000 = 6,4. 9. По табл.1, являющейся фрагментом таблицы, приведенной в [18], перевести QM в уровень sigma: получился уровень 4 sigma, т.е. средний уровень.   Таблица 1 Практическое занятие № 4 На тему «Статистические методы управления процессами»   Раздаточный материал   Статистическое регулирование качества продукции представляет собой корректирование технологического процесса по результатам выборочного контроля параметров изделий до того, как отклонения приведут к браку. Техническим вспомогательным средством статистического регулирования является контрольная карта (КК). В зависимости от назначения продукции и методов её изготовления разработаны соответствующие виды КК. Различают КК по количественным и по качественным признакам. Среди КК по количественным признакам применяются: · карта - карта индивидуальных значений; · карта - карта средних значений; · карта - карта медиан; · карта - карта размахов; · карта - карта среднеквадратических отклонений. Больше информации дают комбинированные КК (или дуаль-карты): · карта -средних значений и размахов; · карта -средних значений и среднеквадратичных отклонений Необходимым условием применения карт по количественным признакам является распределения параметров по нормальному закону. При этом по карте судят о настроенности процесса, а по карте  или по карте  - о точности процесса (разбросе данных). Среди карт по количественным признакам применяются: · p – карта – для регистрации доли дефектности (или процента брака) в выборке; · пр – карта числа дефектных единиц; · с – карта - числа дефектов; · u - карта - числа дефектов, приходящихся на единицу продукции. Необходимым условием применения карт по качественным признакам является распределение параметров по закону Пуассона или биномиальному закону. Пример с ответами   Клиенты жалуются, что государственное учреждение слишком долго оформляет выдачу определенного типа разрешений. Начальник учреждения решил собирать данные для проверки продолжительности цикла оформления разрешения на основании пяти обращений, делаемых каждую неделю. При этом были получены следующие результаты:   Неделя Продолжительность (дни)		R
1	36	33	43	51	33	39,2	18
2	31	50	33	54	37	41,0	23
3	43	41	46	26	37	38,6	20
4	41	40	36	56	29	40,4	27
5	34	26	33	42	28	32,6	16
6	59	33	47	51	65	51,0	32
7	31	41	52	38	40	40,4	21
8	40	40	38	65	51	46,8	27
9	25	47	50	61	56	47,8	36
10	37	48	46	61	49	48,2	24
						42,60	24,4

                                                                

    Решение.

    Для объема выборки n = 5 значения ,  и 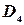 по табл. 1 соответственно равны: 0,577; 0; 2,114.

    В результате имеем:

средний уровень среднего арифметического равен 42,60;

верхнее предельное отклонение для среднего арифметического составляет 42,60 + 0,577ґ24,4 = 56,68;

нижнее предельное отклонение для среднего арифметического составляет 42,60 - 0,577ґ24,4 = 28,52;

средний уровень размаха равен 24,4;

верхнее предельное отклонение для размаха составляет 24,4ґ2,114 = 51,6;

нижнее предельное отклонение для размаха составляет 24,4 ґ 0 = 0.

    Нанесите эти данные на контрольные карты и поясните характер исследуемого процесса.

ВАРИАНТ 1

Клиенты жалуются, что государственное учреждение слишком долго оформляет выдачу определенного типа разрешений. Начальник учреждения решил собирать данные для проверки продолжительности цикла оформления разрешения на основании пяти обращений, делаемых каждую неделю. При этом были получены следующие результаты:

 

Неделя

Продолжительность (дни)

R 1 36 33 43 51 33     2 31 50 33 54 37     3 43 41 46 26 37     4 41 40 36 56 29     5 34 26 33 42 28     6 59 33 47 51 65     7 31 41 52 38 40     8 40 40 38 65 51     9 25 47 50 61 56     10 37 48 46 61 49    

 

                                                                

    Решение.

    Для объема выборки n = 5 значения ,  и  по табл. 1 соответственно равны: 0,577; 0; 2,114.

    В результате имеем:

средний уровень среднего арифметического равен...

верхнее предельное отклонение для среднего арифметического составляет ...

нижнее предельное отклонение для среднего арифметического составляет ...

средний уровень размаха равен ...

верхнее предельное отклонение для размаха составляет...

нижнее предельное отклонение для размаха составляет ...

    Нанесите эти данные на контрольные карты и поясните характер исследуемого процесса.

ВАРИАНТ 2

Клиенты жалуются, что государственное учреждение слишком долго оформляет выдачу определенного типа разрешений. Начальник учреждения решил собирать данные для проверки продолжительности цикла оформления разрешения на основании пяти обращений, делаемых каждую неделю. При этом были получены следующие результаты:

 

Неделя

Продолжительность (дни)

R 1 35 33 47 52 31     2 32 48 36 53 40     3 41 45 39 26 38     4 50 43 32 46 33     5 38 22 39 44 35     6 57 43 58 50 63     7 31 41 52 38 40     8 45 40 34 63 53     9 27 47 51 64 56     10 32 41 49 61 49    

 

                                                                

    Решение.

    Для объема выборки n = 5 значения 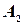,  и  по табл. 1 соответственно равны: 0,577; 0; 2,114.

    В результате имеем:

средний уровень среднего арифметического равен...

верхнее предельное отклонение для среднего арифметического составляет ...

нижнее предельное отклонение для среднего арифметического составляет ...

средний уровень размаха равен ...

верхнее предельное отклонение для размаха составляет...

нижнее предельное отклонение для размаха составляет ...

    Нанесите эти данные на контрольные карты и поясните характер исследуемого процесса.

ВАРИАНТ 3

Клиенты жалуются, что государственное учреждение слишком долго оформляет выдачу определенного типа разрешений. Начальник учреждения решил собирать данные для проверки продолжительности цикла оформления разрешения на основании пяти обращений, делаемых каждую неделю. При этом были получены следующие результаты:

 

Неделя

Продолжительность (дни)

R 1 32 39 40 51 31     2 41 53 50 54 39     3 40 45 47 28 42     4 39 37 32 56 39     5 30 29 28 43 27     6 57 31 41 54 63     7 42 48 55 37 40     8 49 29 39 66 55     9 30 30 51 60 43     10 33 49 42 58 36    

 

                                                                

    Решение.

    Для объема выборки n = 5 значения 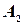,  и  по табл. 1 соответственно равны: 0,577; 0; 2,114.

    В результате имеем:

средний уровень среднего арифметического равен...

верхнее предельное отклонение для среднего арифметического составляет ...

нижнее предельное отклонение для среднего арифметического составляет ...

средний уровень размаха равен ...

верхнее предельное отклонение для размаха составляет...

нижнее предельное отклонение для размаха составляет ...

    Нанесите эти данные на контрольные карты и поясните характер исследуемого процесса.

ВАРИАНТ 4

Клиенты жалуются, что государственное учреждение слишком долго оформляет выдачу определенного типа разрешений. Начальник учреждения решил собирать данные для проверки продолжительности цикла оформления разрешения на основании пяти обращений, делаемых каждую неделю. При этом были получены следующие результаты:

 

Неделя

Продолжительность (дни)

R 1 29 37 43 49 37     2 51 33 50 53 31     3 41 35 49 38 50     4 36 39 41 56 27     5 30 25 38 43 29     6 51 32 48 34 60     7 41 50 55 38 30     8 43 29 39 66 55     9 38 31 55 60 43     10 29 27 40 57 26    

 

                                                                

Решение.

    Для объема выборки n = 5 значения 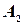,  и  по табл. 1 соответственно равны: 0,577; 0; 2,114.

    В результате имеем:

средний уровень среднего арифметического равен...

верхнее предельное отклонение для среднего арифметического составляет ...

нижнее предельное отклонение для среднего арифметического составляет ...

средний уровень размаха равен ...

верхнее предельное отклонение для размаха составляет...

нижнее предельное отклонение для размаха составляет ...

 

    Нанесите эти данные на контрольные карты и поясните характер исследуемого процесса.

 

ВАРИАНТ 5

Клиенты жалуются, что государственное учреждение слишком долго оформляет выдачу определенного типа разрешений. Начальник учреждения решил собирать данные для проверки продолжительности цикла оформления разрешения на основании пяти обращений, делаемых каждую неделю. При этом были получены следующие результаты:

 

Неделя

Продолжительность (дни)

R 1 39 42 53 44 35     2 50 29 47 43 33     3 40 35 49 38 50     4 39 46 41 56 27     5 35 27 37 40 27     6 52 41 49 54 61     7 40 52 52 38 30     8 49 31 33 61 50     9 29 35 55 59 45     10 28 29 40 53 27    

 

                                                                

Решение.

Для объема выборки n = 5 значения 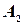,  и  по табл. 1 соответственно равны: 0,577; 0; 2,114.

В результате имеем:

средний уровень среднего арифметического равен ...

верхнее предельное отклонение для среднего арифметического составляет ...

нижнее предельное отклонение для среднего арифметического составляет ...

средний уровень размаха равен ...

верхнее предельное отклонение для размаха составляет ...

нижнее предельное отклонение для размаха составляет ...

 

Нанесите эти данные на контрольные карты и поясните характер исследуемого процесса.

Практическое занятие № 5

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: