Соответствие между углами и числовым рядом
Тригонометрия
Наталья Сергеевна Шабрыкина
Углы и их измерение
Пусть даны два совпадающих луча  - подвижный и
- подвижный и 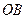 - неподвижный. И пусть луч
- неподвижный. И пусть луч  поворачиваясь в плоскости вокруг точки
поворачиваясь в плоскости вокруг точки  , совершит некоторый поворот. Такой поворот, при котором луч
, совершит некоторый поворот. Такой поворот, при котором луч  впервые опять совпадет с лучом
впервые опять совпадет с лучом 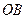 , называется полным оборотом.
, называется полным оборотом.
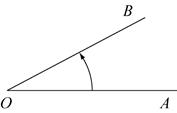
Пусть луч  совершил некоторый поворот, тогда говорят, что он задает угол
совершил некоторый поворот, тогда говорят, что он задает угол  , соответствующий этому повороту. Другим определением угла является геометрическая фигура, образованная двумя лучами, исходящими из одной точки
, соответствующий этому повороту. Другим определением угла является геометрическая фигура, образованная двумя лучами, исходящими из одной точки  , которая называется вершиной угла. Луч
, которая называется вершиной угла. Луч 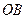 носит название начала отсчета и обычно направлен горизонтально вправо.
носит название начала отсчета и обычно направлен горизонтально вправо.
Для измерения углов применяют две меры.
Градусная мера угла
Поворот, равный  полного оборота против часовой стрелки задает угол в один градус. Различают также следующие доли градуса: 1 минута = 1’ = 1/60 градуса; 1 секунда = 1’’ = 1/60 минуты = 1/3600 градуса.
полного оборота против часовой стрелки задает угол в один градус. Различают также следующие доли градуса: 1 минута = 1’ = 1/60 градуса; 1 секунда = 1’’ = 1/60 минуты = 1/3600 градуса.
Угол, равный 180о или половине полного оборота называют развернутым, равный 90о или четверти полного оборота – прямым.
Радианная мера угла
Рассмотрим два луча  - подвижный и
- подвижный и 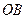 - неподвижный. Выберем на них точки
- неподвижный. Выберем на них точки  и
и 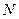 , которые в начальный момент времени совпадают. При повороте точка
, которые в начальный момент времени совпадают. При повороте точка  будет описывать окружность радиуса
будет описывать окружность радиуса 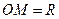 . Повернем подвижный луч
. Повернем подвижный луч  так, чтобы точка
так, чтобы точка  прошла расстояние, равное радиусу:
прошла расстояние, равное радиусу:  , тогда луч
, тогда луч  составит с лучом
составит с лучом 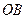 угол в один радиан.
угол в один радиан.

Если повернуть подвижный луч  так, чтобы точка
так, чтобы точка  прошла расстояние
прошла расстояние  , тогда луч
, тогда луч  составит с лучом
составит с лучом 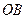 угол в
угол в  радиан.
радиан.
При совершение полного оборота точка  проходит расстояние, равное длине окружности
проходит расстояние, равное длине окружности 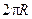 , значит полный оборот соответствует углу
, значит полный оборот соответствует углу 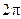 радиан.
радиан.
Из вышесказанного нетрудно установить, что радиан соответствует 180о. Таким образом,  и
и 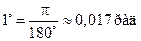 .
.
Соответствие между углами и числовым рядом
Радианная мера угла позволяет установить взаимно однозначное соответствие между множеством углов и рядом действительных чисел. Это возможно, поскольку с одной стороны  - это число, равное 3, 14… с другой стороны это угол, соответствующий 180о. Таким образом, нетрудно установить взаимооднозначное соответствие между углами от 0 до 360о и действительными числами от 0 до
- это число, равное 3, 14… с другой стороны это угол, соответствующий 180о. Таким образом, нетрудно установить взаимооднозначное соответствие между углами от 0 до 360о и действительными числами от 0 до 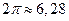 . Для того, чтобы понять, как поставить в соответствие углы числам, превышающим
. Для того, чтобы понять, как поставить в соответствие углы числам, превышающим  , следует вспомнить, что совершив полный оборот подвижный луч возвращается в исходное положение, т.е. любым углам, различающимся на
, следует вспомнить, что совершив полный оборот подвижный луч возвращается в исходное положение, т.е. любым углам, различающимся на  или кратное им будет соответствовать одно и то же взаимное положение подвижного или неподвижного лучей. Отрицательные же углы соответствуют повороту подвижного луча против часовой стрелки. Таким образом, любое действительное число представляет собой радианную меру какого-либо угла и наоборот, любому углу можно поставить в соответствие действительное число.
или кратное им будет соответствовать одно и то же взаимное положение подвижного или неподвижного лучей. Отрицательные же углы соответствуют повороту подвижного луча против часовой стрелки. Таким образом, любое действительное число представляет собой радианную меру какого-либо угла и наоборот, любому углу можно поставить в соответствие действительное число.
Тригонометрические функции
Определения
Определения тригонометрическим функциям даются с помощью тригонометрической окружности, под которой понимается окружность единичного радиуса с центром в начале координат.

Рассмотрим два радиуса этой окружности: неподвижный 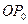 (где точка
(где точка  ) и подвижный
) и подвижный 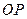 (где точка
(где точка 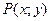 ). Пусть подвижный радиус образует с неподвижным угол
). Пусть подвижный радиус образует с неподвижным угол  .
.
Число, равное ординате конца единичного радиуса, образующего угол  с неподвижным радиусом
с неподвижным радиусом 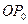 , называется синусом угла
, называется синусом угла  :
:  .
.
Число, равное абсциссе конца единичного радиуса, образующего угол  с неподвижным радиусом
с неподвижным радиусом 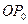 , называется косинусом угла
, называется косинусом угла  :
: 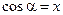 .
.
Таким образом, точка 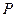 , являющаяся концом подвижного радиуса, образующего угол
, являющаяся концом подвижного радиуса, образующего угол  , имеет координаты
, имеет координаты 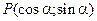 .
.
Тангенсом угла  называется отношение синуса этого угла к его косинусу:
называется отношение синуса этого угла к его косинусу:  ,
,  ,
, 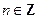 .
.
Котангенсом угла  называется отношение косинуса этого угла к его синусу:
называется отношение косинуса этого угла к его синусу: 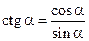 ,
, 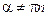 ,
, 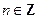 .
.
Четность/нечетность
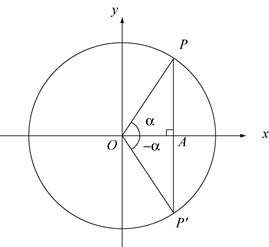
Рассмотрим тригонометрические функции двух углов  (который соответствует подвижному радиусу
(который соответствует подвижному радиусу  ) и
) и 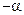 (который соответствует подвижному радиусу
(который соответствует подвижному радиусу  ). Поскольку
). Поскольку 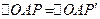 , значит точка
, значит точка  имеет координаты
имеет координаты  . Поэтому
. Поэтому 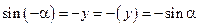 , т.е. синус – функция нечетная;
, т.е. синус – функция нечетная; 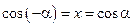 , т.е. косинус – функция четная;
, т.е. косинус – функция четная;  , т.е. тангенс нечетен;
, т.е. тангенс нечетен;  , т.е. котангенс также нечетен.
, т.е. котангенс также нечетен.
Промежутки знакопостоянства
Знаки тригонометрических функций для различных координатных четвертей следуют из определения этих функций. Следует отметить, что поскольку тангенс и котангенс являются отношениями синуса и косинуса, они положительны, когда синус и косинус угла имеют одинаковые знаки и отрицательны когда разные.
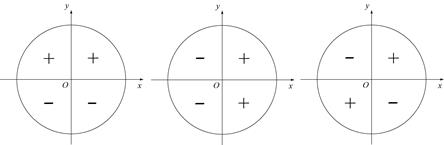
синус косинус тангенс, котангенс
Периодичность
Периодичность синуса и косинуса основана на том факте, что углы, отличающиеся на целое количество полных оборотов, соответствуют одному и тому же взаимному расположению подвижного и неподвижного лучей. Соответственно и координаты точки пересечения подвижного луча и тригонометрической окружности будут одинаковы для углов, отличающихся на целое количество полных оборотов. Таким образом, периодом синуса и косинуса является 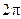 и
и 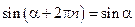 ,
, 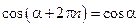 , где
, где 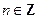 .
.
Очевидно, что 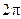 также является периодом для тангенса и котангенса. Но существует ли меньший период для этих функций? Докажем, что наименьшим периодом для тангенса и котангенса является
также является периодом для тангенса и котангенса. Но существует ли меньший период для этих функций? Докажем, что наименьшим периодом для тангенса и котангенса является  .
.

Рассмотрим два угла  и
и 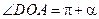 . Оп геометрическому смыслу тангенса и котангенса
. Оп геометрическому смыслу тангенса и котангенса 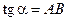 ,
, 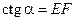 ,
,  ,
, 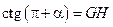 . По стороне и прилежащим к ней углам равны треугольники
. По стороне и прилежащим к ней углам равны треугольники 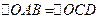 и
и  , значит равны и их стороны, значит
, значит равны и их стороны, значит 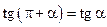 и
и 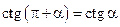 . Аналогичным образом можно доказать, то
. Аналогичным образом можно доказать, то 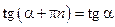 ,
, 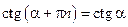 , где
, где 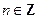 . Таким образом, периодом тангенса и котангенса является
. Таким образом, периодом тангенса и котангенса является  .
.
Формулы тригонометрии
Для успешного решения тригонометрических задач необходимо владеть многочисленными тригонометрическими формулами. Тем не менее, нет необходимости заучивать все формулы. Знать наизусть нужно лишь самые основные, а остальные формулы нужно уметь при необходимости вывести.
Формулы приведения
С помощью формул приведения можно выразить значения тригонометрических функций произвольных углов через значения функций острого угла. Все формулы приведения могут быть обобщены с помощью следующего правила.
Любая тригонометрическая функция угла  ,
, 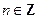 по абсолютной величине равна той же функции угла
по абсолютной величине равна той же функции угла  , если число
, если число  – четное, и ко-функции угла
– четное, и ко-функции угла  , если число
, если число  – нечетное. При этом если функция угла
– нечетное. При этом если функция угла  ,
, 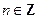 положительна, когда
положительна, когда  – острый положительный угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
– острый положительный угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
Определения
До сих пор мы решали задачу определения тригонометрических функций заданных углов. А что если стоит обратная задача: зная какую-либо тригонометрическую функцию определить соответствующий ей угол.
Арксинус
Рассмотрим выражение  , где
, где 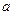 – известное вещественное число. По определению синуса это есть ордината точки пересечения луча, образующего угол
– известное вещественное число. По определению синуса это есть ордината точки пересечения луча, образующего угол 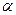 с осью абсцисс и тригонометрической окружности. Таким образом, для решения уравнения
с осью абсцисс и тригонометрической окружности. Таким образом, для решения уравнения  надо найти точки пересечения прямой
надо найти точки пересечения прямой 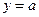 и тригонометрической окружности.
и тригонометрической окружности.

Очевидно, что при  прямая и окружность не имеют общих точек, а значит и уравнение
прямая и окружность не имеют общих точек, а значит и уравнение  не имеет решений. То есть нельзя найти угол, синус которого был бы по модулю больше 1.
не имеет решений. То есть нельзя найти угол, синус которого был бы по модулю больше 1.
При  прямая и окружность имеют точки пересечения, например,
прямая и окружность имеют точки пересечения, например, 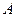 и
и 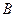 (см. рис.). Таким образом, заданный синус будут иметь
(см. рис.). Таким образом, заданный синус будут иметь 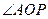 ,
, 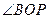 и все углы, отличающиеся от них на целое количество полных оборотов, т.е.
и все углы, отличающиеся от них на целое количество полных оборотов, т.е. 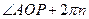 ,
, 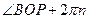 ,
, 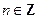 – бесконечное множество углов. Как выбрать один угол среди этого бесконечного множества?
– бесконечное множество углов. Как выбрать один угол среди этого бесконечного множества?
Чтобы однозначно определить угол 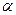 , соответствующий числу
, соответствующий числу 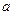 , приходится требовать выполнения дополнительного условия: этот угол должен принадлежать отрезку
, приходится требовать выполнения дополнительного условия: этот угол должен принадлежать отрезку 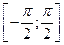 . Такой угол
. Такой угол 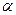 называют арксинусом числа
называют арксинусом числа 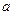 .
.
Арксинусом действительного числа 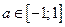 называется действительное число
называется действительное число 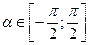 , синус которого равен
, синус которого равен 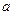
 . Такое число обозначают
. Такое число обозначают 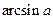 .
.
Арккосинус
Рассмотрим теперь уравнение вида  . Для его решения необходимо найти на тригонометрической окружности все точки, имеющие абсциссу
. Для его решения необходимо найти на тригонометрической окружности все точки, имеющие абсциссу 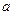 , т.е. точки пересечения с прямой
, т.е. точки пересечения с прямой 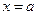 . Как и в предыдущем случае при
. Как и в предыдущем случае при  рассматриваемое уравнение не имеет решений. А если
рассматриваемое уравнение не имеет решений. А если 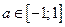 , имеются точки пересечения прямой и окружности, соответствующие бесконечному множеству углов
, имеются точки пересечения прямой и окружности, соответствующие бесконечному множеству углов 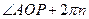 ,
, 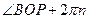 ,
, 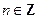 .
.

Чтобы однозначно определить угол 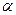 , соответствующий данному косинусу, вводят дополнительное условие: этот угол должен принадлежать отрезку
, соответствующий данному косинусу, вводят дополнительное условие: этот угол должен принадлежать отрезку  ; такой угол называют арккосинусом числа
; такой угол называют арккосинусом числа 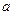 .
.
Арккосинусом действительного числа 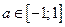 называется действительное число
называется действительное число  , косинус которого равен
, косинус которого равен 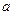
 . Такое число обозначают
. Такое число обозначают  .
.
Арктангенс и арккотангенс
Рассмотрим выражение 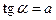 . Для его решения надо найти на окружности все точки пересечения с прямой
. Для его решения надо найти на окружности все точки пересечения с прямой 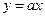 , угловой коэффициент которой равен тангенсу угла наклона прямой к положительному направлению оси абсцисс. Такая прямая при всех действительных значениях
, угловой коэффициент которой равен тангенсу угла наклона прямой к положительному направлению оси абсцисс. Такая прямая при всех действительных значениях 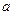 пересекает тригонометрическую окружность в двух точках. Эти точки симметричны относительно начала координат и соответствуют углам
пересекает тригонометрическую окружность в двух точках. Эти точки симметричны относительно начала координат и соответствуют углам 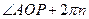 ,
, 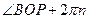 ,
, 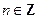 .
.
Для однозначного определения угла с заданным тангенсом его выбирают из интервала  .
.

Арктангенсом произвольного действительного числа 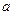 называется действительное число
называется действительное число 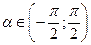 , тангенс которого равен
, тангенс которого равен 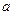
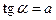 . Такое число обозначают
. Такое число обозначают  .
.
Для определения арккотангенса угла используются аналогичные рассуждения, с той лишь разницей, что рассматривается пересечение окружности с прямой 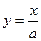 и угол выбирается из интервала
и угол выбирается из интервала 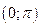 .
.
Арккотангенсом произвольного действительного числа 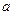 называется действительное число
называется действительное число  , котангенс которого равен
, котангенс которого равен 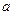
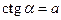 . Такое число обозначают
. Такое число обозначают  .
.
Четность/нечетность
Список литературы
Тригонометрия
Наталья Сергеевна Шабрыкина
Углы и их измерение
Пусть даны два совпадающих луча  - подвижный и
- подвижный и 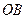 - неподвижный. И пусть луч
- неподвижный. И пусть луч  поворачиваясь в плоскости вокруг точки
поворачиваясь в плоскости вокруг точки  , совершит некоторый поворот. Такой поворот, при котором луч
, совершит некоторый поворот. Такой поворот, при котором луч  впервые опять совпадет с лучом
впервые опять совпадет с лучом 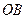 , называется полным оборотом.
, называется полным оборотом.

Пусть луч  совершил некоторый поворот, тогда говорят, что он задает угол
совершил некоторый поворот, тогда говорят, что он задает угол  , соответствующий этому повороту. Другим определением угла является геометрическая фигура, образованная двумя лучами, исходящими из одной точки
, соответствующий этому повороту. Другим определением угла является геометрическая фигура, образованная двумя лучами, исходящими из одной точки  , которая называется вершиной угла. Луч
, которая называется вершиной угла. Луч 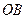 носит название начала отсчета и обычно направлен горизонтально вправо.
носит название начала отсчета и обычно направлен горизонтально вправо.
Для измерения углов применяют две меры.
Градусная мера угла
Поворот, равный  полного оборота против часовой стрелки задает угол в один градус. Различают также следующие доли градуса: 1 минута = 1’ = 1/60 градуса; 1 секунда = 1’’ = 1/60 минуты = 1/3600 градуса.
полного оборота против часовой стрелки задает угол в один градус. Различают также следующие доли градуса: 1 минута = 1’ = 1/60 градуса; 1 секунда = 1’’ = 1/60 минуты = 1/3600 градуса.
Угол, равный 180о или половине полного оборота называют развернутым, равный 90о или четверти полного оборота – прямым.
Радианная мера угла
Рассмотрим два луча  - подвижный и
- подвижный и 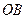 - неподвижный. Выберем на них точки
- неподвижный. Выберем на них точки  и
и 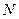 , которые в начальный момент времени совпадают. При повороте точка
, которые в начальный момент времени совпадают. При повороте точка  будет описывать окружность радиуса
будет описывать окружность радиуса 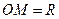 . Повернем подвижный луч
. Повернем подвижный луч  так, чтобы точка
так, чтобы точка  прошла расстояние, равное радиусу:
прошла расстояние, равное радиусу:  , тогда луч
, тогда луч  составит с лучом
составит с лучом 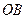 угол в один радиан.
угол в один радиан.

Если повернуть подвижный луч  так, чтобы точка
так, чтобы точка  прошла расстояние
прошла расстояние  , тогда луч
, тогда луч  составит с лучом
составит с лучом 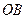 угол в
угол в  радиан.
радиан.
При совершение полного оборота точка  проходит расстояние, равное длине окружности
проходит расстояние, равное длине окружности 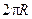 , значит полный оборот соответствует углу
, значит полный оборот соответствует углу 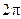 радиан.
радиан.
Из вышесказанного нетрудно установить, что радиан соответствует 180о. Таким образом,  и
и 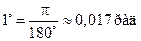 .
.
Соответствие между углами и числовым рядом
Радианная мера угла позволяет установить взаимно однозначное соответствие между множеством углов и рядом действительных чисел. Это возможно, поскольку с одной стороны  - это число, равное 3, 14… с другой стороны это угол, соответствующий 180о. Таким образом, нетрудно установить взаимооднозначное соответствие между углами от 0 до 360о и действительными числами от 0 до
- это число, равное 3, 14… с другой стороны это угол, соответствующий 180о. Таким образом, нетрудно установить взаимооднозначное соответствие между углами от 0 до 360о и действительными числами от 0 до 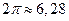 . Для того, чтобы понять, как поставить в соответствие углы числам, превышающим
. Для того, чтобы понять, как поставить в соответствие углы числам, превышающим  , следует вспомнить, что совершив полный оборот подвижный луч возвращается в исходное положение, т.е. любым углам, различающимся на
, следует вспомнить, что совершив полный оборот подвижный луч возвращается в исходное положение, т.е. любым углам, различающимся на  или кратное им будет соответствовать одно и то же взаимное положение подвижного или неподвижного лучей. Отрицательные же углы соответствуют повороту подвижного луча против часовой стрелки. Таким образом, любое действительное число представляет собой радианную меру какого-либо угла и наоборот, любому углу можно поставить в соответствие действительное число.
или кратное им будет соответствовать одно и то же взаимное положение подвижного или неподвижного лучей. Отрицательные же углы соответствуют повороту подвижного луча против часовой стрелки. Таким образом, любое действительное число представляет собой радианную меру какого-либо угла и наоборот, любому углу можно поставить в соответствие действительное число.
Тригонометрические функции
Определения
Определения тригонометрическим функциям даются с помощью тригонометрической окружности, под которой понимается окружность единичного радиуса с центром в начале координат.

Рассмотрим два радиуса этой окружности: неподвижный 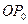 (где точка
(где точка  ) и подвижный
) и подвижный 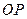 (где точка
(где точка 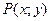 ). Пусть подвижный радиус образует с неподвижным угол
). Пусть подвижный радиус образует с неподвижным угол  .
.
Число, равное ординате конца единичного радиуса, образующего угол  с неподвижным радиусом
с неподвижным радиусом 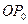 , называется синусом угла
, называется синусом угла  :
:  .
.
Число, равное абсциссе конца единичного радиуса, образующего угол  с неподвижным радиусом
с неподвижным радиусом 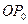 , называется косинусом угла
, называется косинусом угла  :
: 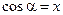 .
.
Таким образом, точка 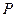 , являющаяся концом подвижного радиуса, образующего угол
, являющаяся концом подвижного радиуса, образующего угол  , имеет координаты
, имеет координаты 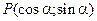 .
.
Тангенсом угла  называется отношение синуса этого угла к его косинусу:
называется отношение синуса этого угла к его косинусу:  ,
,  ,
, 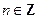 .
.
Котангенсом угла  называется отношение косинуса этого угла к его синусу:
называется отношение косинуса этого угла к его синусу: 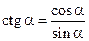 ,
, 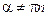 ,
, 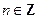 .
.
Популярное:

