Смысл и измерение параметров рассеяния

Нормализация токов и напряжений

Многополюсник почти всегда можно рассматривать как сочленение линий передачи (вопрос, собственно, в том, можно ли рассматривать связи многополюсника с остальной частью устройства как длинные линии, например, достаточно ли они длинные для затухания «лишних» мод, и т. п.). Для данного типа монохроматической волны распределение поперечных составляющих напряженности электрического поля в любом сечении однородной линии передачи одинаково (с точностью до амплитуды) [10.8]. Мощность , переносимая падающей волной в однородной линии без потерь равна

где – поперечные (к оси линии передачи) составляющие комплексных амплитуд векторов электрического и магнитного полей;

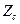– характеристическое сопротивление линии передачи для данного типа волны;

– векторное произведение векторов и ;

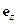– единичный вектор в направлении оси ;

интегрирование ведется по поперечному сечению линии.

Нормированные электрическая и магнитная напряженности вводятся так, чтобы

тогда, в силу одинаковости распределения по сечению при разных , можно записать

где – размерные коэффициенты нормировки;

– эквивалентные напряжение и ток в линии передачи, пропорциональные, как видим, амплитудам напряженностей электрического и магнитного полей, соответственно, и называемые интегральными параметрами линии передачи.

Введем также эквивалентные волновые сопротивления по напряжению и току:

Пары коэффициентов нормировки можно выбрать по-разному, задавая тем самым различные нормировки полей и эквивалентных напряжения и тока. Из соображений удобства записи формул наиболее часто выбирают

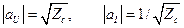
(предполагается, что характеристическое сопротивление линии передачи действительно). В получаемой при таком выборе коэффициентов нормировке эквивалентные напряжение и ток называются нормализованными и обозначаются 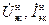, а волновые сопротивления .

Из вышеприведенных соотношений легко получить формулу для переносимой мощности:

(10.4.1)

откуда следует, что нормализованные напряжение и ток имеют одинаковую размерность 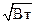. Все это дает право рассматривать нормализованную волну с комплексными амплитудами напряжения и тока 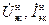как волну мощности [10.3].

Введение параметров рассеяния (илл. Осн анал цепей, с. 24, с. 28, с. 29, 30(таб))

Рассмотрим -полюсник ( -портовое устройство, -плечное устройство) как сочленение линий передачи. Внутренняя структура многополюсника может быть как угодно сложной, при возбуждении его со стороны одной или нескольких линий внутри сочленения возникает как угодно сложное электромагнитное поле, но нас интересуют лишь соотношения между первичными и вторичными параметрами многополюсника. В общем случае подводящие к сочленению линии передачи могут быть разного типа (волноводного, коаксиального, полоскового), разной конструкции, разных характерных размеров, иметь разные постоянные распространения, в них могут распространяться различные наборы мод и т. д. Для большей ясности изложения будем считать, что подводящие линии передачи однородны, без потерь, одной конструкции, с одномодовым переносом волны и одинаковым коэффициентом фазы на данной частоте. От некоторых из этих ограничений можно отказаться, например, при переносе по линии нескольких независимых мод следует заменить эту линию на соответствующее число линий со своими постоянными распространения. Однако нам подобные обобщения не понадобятся.

Выберем и зафиксируем на каждой подводящей линии передачи некую плоскость поперечного сечения (плоскость отсчета фаз, опорная плоскость), находящуюся на своем электрическом расстоянии 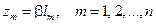от одной условной точки (центр) сочленения. Величины должны быть достаточно большими, чтобы нежелательные моды волн на их протяжении сильно затухали. Выбранные плоскостей отсчета фаз являются одновременно входами и выходами (портами) -полюсника. Условимся называть падающими (входящими) волны, распространяющиеся в сторону сочленения, и отраженными (выходящими) – распространяющиеся от сочленения. В общем случае на каждом из портов есть одна падающая и одна отраженная волны (в частном случае некоторые падающие волны могут отсутствовать).

В соответствии с ранее принятыми обозначениями, комплексные амплитуды нормализованных падающих и отраженных волн напряжений и токов пришлось бы теперь записывать так:

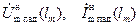и т. д.

где учтено, что они зависят от параметров . Для упрощения записи введем переобозначения:

, .

В новых обозначениях зависимости от не показаны явно, однако следует помнить, что комплексные амплитуды нормализованных волн относятся к выбранным опорным плоскостям, которые далее называются портами. Согласно (10.4.1), мощности падающей и отраженной волн в плече :

поэтому могут называться волнами мощности.

Как и в изложенных выше классических матричных описаниях -портовой линейной цепи, мы нуждаемся в параметрах возбужденной цепи, которые можно разделить на две группы по параметров в каждой, и установить независимых линейных соотношений между элементами этих групп. Возьмем в качестве первичных параметров возбужденной цепи падающие волны, а в качестве вторичных – отраженные волны (в этом принципиальное отличие нового описания от классических систем, где в качестве параметров фигурировали токи и напряжения). Отметим принципиальный момент: поскольку полное напряжение в каждом порте равно (векторной) сумме падающей и отраженной волн напряжения, то совокупность всех волн напряжения возбужденного многополюсника представляет собой линейную систему; аналогично обстоит дело и с волнами тока.

Образуем -мерные нормализованные векторы-столбцы падающих и отраженных волн напряжения:

; ,

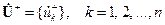тогда линейное соотношение между этими векторами (основная система равенств -полюсника) запишется в виде:

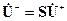(10.5.1)

или в расписанном виде

…………………………….. ……………………………..

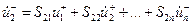(10.5.2)

В равенствах (10.5.1), (10.5.2): – квадратная комплекснозначная матрица 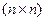, называемая матрицей рассеяния ( -матрицей, волновой матрицей); комплексные безразмерные величины 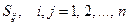– элементы матрицы рассеяния, называемые параметрами рассеяния ( 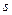-параметрами). Заметим, что, поскольку нормализованные волны относятся к опорным плоскостям, то и связывающие их параметры рассеяния также относятся к этим плоскостям, и при изменении положения этих плоскостей параметры рассеяния, вообще говоря, меняются.

Можно, наоборот, выразить вектор падающих волн через вектор отраженных волн:

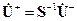
(10.5.3)

при условии, что матрица рассеяния не особенная, т. е. что .

Так же как каждая классическая матрица линейного многополюсника, матрица рассеяния полностью описывает свойства последнего на данной частоте возбуждения. Рассмотрев произвольную -ую строку системы, видим, что нормализованная отраженная волна на -ом порте равна взвешенной векторной сумме падающих волн на всех портах, а элементы -ой строки матрицы рассеяния суть комплексные веса в этой сумме.

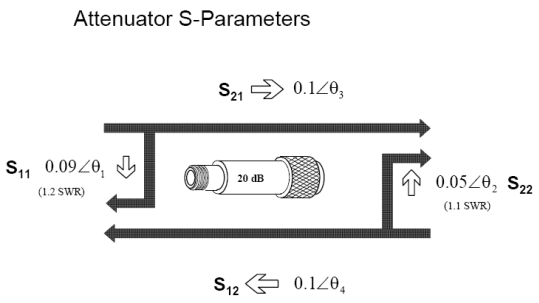
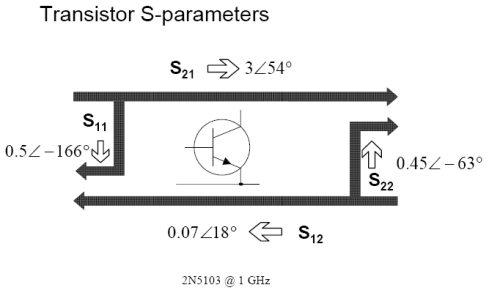
Смысл параметров рассеяния

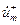Пусть -полюсник возбуждается только из -го порта ( =1, 2, …, ) падающей волной , а остальные порты нагружены на согласованные нагрузки. Так как коэффициент отражения от согласованной нагрузки равен нулю, то в остальные плечи многополюсника энергия не поступает, т. е. все падающие волны, кроме -ой, равны нулю. Тогда от системы (10.5.2) остается только «столбцовая» система

(10.6.1)

показывающая, что под действием такого возбуждения в сочленении возникает электромагнитное поле, в свою очередь возбуждающее выходящие из сочленения (отраженные) волны, все пропорциональные одной и той же падающей волне 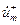, но с разными (в общем случае – комплексными) коэффициентами пропорциональности 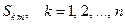. С математической точки зрения коэффициенты 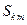суть элементы -го столбца матрицы рассеяния , с физической – они зависят от внутренней структуры многополюсника и положения плоскостей отсчета.

Поскольку аналогичные соотношения можно записать при возбуждении многополюсника со стороны других плеч (выбор любого в пределах от 1 до ), при согласовании остальных плеч, соотношение (10.6.1) дает возможность одновременно выяснить физический смысл параметров рассеяния и найти принципиальный метод их измерения. При 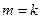из (10.6.1) получаем:

(10.6.2)

т. е. диагональные элементы матрицы рассеяния суть (комплексные) коэффициенты отражения в плоскостях отсчета соответственных плеч, и принципиальный способ измерения диагональных элементов – измерения соответствующих коэффициентов отражения в условиях согласования всех плеч, кроме измеряемого.

При из (10.6.1) получаем:

(10.6.3)

т. е. недиагональный элемент 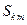матрицы рассеяния суть (комплексный) коэффициент передачи из плеча в плечо , при условии, что к плечу подключен генератор, а все остальные плечи согласованы; принципиальный способ измерения этого элемента – измерение названного коэффициента передачи при условии всех названных согласований. Во избежание путаницы подчеркнем еще раз: первый индекс недиагонального матричного элемента – номер плеча, в который направлен коэффициент передачи, второй индекс – номер возбуждаемого плеча.

Измерение параметров рассеяния

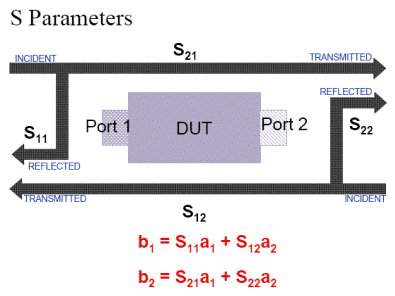
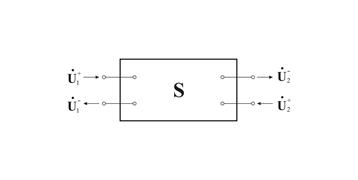
Рассмотрим частный случай четырехполюсника (двухпортовой цепи), =2 (рис. 10.6.1). Основная система равенств в терминах параметров рассеяния имеет вид:

,	(10.6.4)
,	(10.6.5)

– (комплексный) коэффициент отражения на входе (в порте 1) при согласовании на выходе (в порте 2);

– (комплексный) коэффициент отражения на выходе (в порте 2) при согласовании на входе (в порте 1);

– (комплексный) коэффициент передачи из порта 1 в порт 2 при согласовании на выходе (в порте 2);

– (комплексный) коэффициент передачи из порта 2 в порт 1 при согласовании на входе (в порте 1).

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒