Элементы симметрии додекаэдра

Додекаэдр имеет центр симметрии и 15 осей симметрии. Каждая из осей проходит через середины противолежащих параллельных ребер.
Додекаэдр имеет 15 плоскостей симметрии. Любая из плоскостей симметрии проходит в каждой грани через вершину и середину противоположного ребра.

Интересные факты

Форму, близкую к додекаэдру имеет описанная Эрнстом Геккелем в 1887 году радиолярия Circorrhegma dodecahedra^[10].
В 2003 году, при анализе данных космического аппарата WMAP, была выдвинута гипотеза, что Вселенная представляет собой додекаэдрическое пространство Пуанкаре^[11][12][13].

В культуре

Додекаэдр применяется как генератор случайных чисел (вместе с другими костями) в настольных ролевых играх, и обозначается при этом d12 (dice — кости).
Изготавливаются настольные календари в форме додекаэдра из бумаги, где каждый из двенадцати месяцев расположен на одной из граней.
В игре Пентакор мир представлен в виде этой геометрической фигуры.
В играх " Соник 3" и " Соник и Кнаклз" вид додекаэдра имеют изумруды хаоса.

Икосаэдр

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 сентября 2013; проверки требуют 15 правок.

Икосаэдр

Тип	Правильный многогранник
Грань	Правильный треугольник
Граней
Рёбер
Вершин
Граней при вершине
Группа симметрии	Икосаэдрическая (I_h)
Двойственный многогранник	додекаэдр

Развертка икосаэдра

Икосаэдр и его описанная сфера

Икоса́ эдр (от др.-греч. ε ἴ κ ο σ ι «двадцать»; ἕ δ ρ ο ν «сидение», «основание») — правильный выпуклый многогранник, двадцатигранник ^[1], одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.

Содержание

1 История
2 Основные формулы
3 Свойства
4 Усечённый икосаэдр
5 В мире

5.1 Тела в виде икосаэдра

6 См. также
7 Примечания
8 Литература

История

Евклид в предложении 16 книги XIII «Начал» занимается построением икосаэдра, получая сначала два правильных пятиугольника, лежащих в двух параллельных плоскостях — из десяти его вершин, и затем — две оставшиеся противоположные друг другу вершины^{[2][3]: 127-131}. Папп Александрийский в «Математическом собрании» занимается построением икосаэдра, вписанного в данную сферу, попутно доказывая, что двенадцать его вершин лежат в четырех параллельных плоскостях, образуя в них четыре правильных треугольника^{[4][3]: 315-316}.

Основные формулы

Площадь поверхности S, объём V икосаэдра с длиной ребра a, а также радиусы вписанной и описанной сфер вычисляются по формулам:

Площадь:

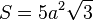
Объём:

Радиус вписанной сферы^[5]:

Радиус описанной сферы^[5]:

Свойства

Все двенадцать вершин икосаэдра лежат по три в четырёх параллельных плоскостях, образуя в каждой из них правильный треугольник.
Десять вершин икосаэдра лежат в двух параллельных плоскостях, образуя в них два правильных пятиугольника, а остальные две — противоположны друг другу и лежат на двух концах диаметра описанной сферы, перпендикулярного этим плоскостям.
Икосаэдр можно вписать в куб, при этом шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
В икосаэдр может быть вписан тетраэдр, так что четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12× 5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12× 5=90.
Собрать модель икосаэдра можно при помощи 20 тетраэдров.
Невозможно собрать икосаэдр из правильных тетраэдров, так как радиус описанной сферы вокруг икосаэдра, соответственно и длина бокового ребра (от вершины до центра такой сборки) тетраэдра меньше ребра самого икосаэдра.

Усечённый икосаэдр

Основная статья: Усечённый икосаэдр

Молекула фуллерена C₆₀ — усечённый икосаэдр

Усечённый икосаэдр — многогранник, состоящий из 12 правильных пятиугольников и 20 правильных шестиугольников. Имеет икосаэдрический тип симметрии. По сути футбольный мяч имеет форму не шара, а усечённого икосаэдра.

⇐ Предыдущая 123 4 5 6 7 8 9 Следующая ⇒