
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Между двумя концентрическими сферами ⇐ ПредыдущаяСтр 7 из 7
На рис. 16.7. изображена исследуемая система.
 Пространство между сферами радиусов Пространство между сферами радиусов  и и 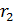 заполнено однородной средой. Поток теплоты через сферическую поверхность радиуса заполнено однородной средой. Поток теплоты через сферическую поверхность радиуса 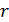 равен равен 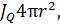 эта величина постоянна и не зависит от радиуса сферы. Поэтому уравнение для плотности потока имеет вид эта величина постоянна и не зависит от радиуса сферы. Поэтому уравнение для плотности потока имеет вид
После интегрирования (16.12) получим
Из граничных условий находим
Ещё раз отметим, что распределения температур в слоях вещества с разной симметрией получены при условии, что
Внешняя теплопередача Внешней теплопередачей называется теплопередача между двумя различными телами, не находящимися в тепловом равновесии друг с другом. Приведем примеры: 1. Процесс охлаждения нагретого металлического тела потоком воды или воздуха. 2. Процесс теплопередачи между отапливаемым домом и окружающим воздухом. Идеализируя ситуацию, можно считать, что в каждый момент времени тело имеет одну и ту же температуру
где Контрольные вопросы 1. Какие процессы называются процессами переноса? Приведите примеры. 2. Почему переход системы к равновесию может характеризоваться несколькими, отличающимися друг от друга временами релаксации? 3. Что называется временем термализации? 4. Почему время релаксации зависит от размеров системы? 5. В чем суть представления о локальном равновесии? 6. Какое уравнение является основой молекулярно-кинетической теории явлений переноса? 7. Какая связь существует между процессами переноса и принципом Ле Шателье-Брауна? 8. Запишите стационарные одномерные уравнения теплопроводности, самодиффузии и внутреннего трения. Какова область их применимости? 9. Какова размерность коэффициентов теплопроводности, самодиффузии и вязкости? 10. Как зависит от координат плотность теплового потока в слое вещества, имеющем плоскую, цилиндрическую и сферическую симметрию? 11. Как используются граничные условия для нахождения распределения температуры в слое вещества? 12. Что называется внешней теплопередачей? Запишите формулу Ньютона, описывающую этот процесс. Какова область её применимости?
ЛЕКЦИЯ 17
ЭЛЕМЕНТАРНАЯ КИНЕТИЧЕСКАЯ ТЕОРИЯ ПРОЦЕССОВ ПЕРЕНОСА В ГАЗАХ Настоящая лекция посвящена раскрытию сущности явлений переноса и нахождению количественных выражений для макроскопических коэффициентов переноса в плотных и ультра разреженных газах. Прежде чем приступить к изложению элементарной теории явлений переноса сконцентрируем свое внимание на рассмотрении столкновений молекул между собой. Именно эти микроскопические процессы играют определяющую роль в механизмах переноса молекулярных свойств, не только в газах, но также в жидкостях и твердых телах.
17.1. Столкновения молекул и их количественные характеристики
Столкновения частиц вещества друг с другом приводят к случайному изменению их кинетических энергий и, в конечном счете, к установлению равновесного распределения молекул по скоростям. Столкновения могут приводить и к другим последствиям. Например, в результате столкновения может произойти ионизация атома, химическая или ядерная реакции и многое другое. Если бы не было столкновений, то распространение запахов в воздухе и выравнивание температур в жидкостях и газах происходило бы практически мгновенно, ведь средние скорости теплового движения молекул равны сотням метров в секунду. В действительности при отсутствии конвективных потоков воздуха или жидкости продолжительность подобных процессов может составлять минуты и часы. Так же медленно происходит выравнивание скоростей макроскопического движения газа или жидкости посредством сил вязкости. Медленность диффузии и аналогичных ей процессов объясняется тем, то в результате непрерывной череды соударений с другими частицами каждая молекула мечется туда и сюда и поэтому её продвижение вперед происходит не по прямой. Вспомните движение броуновской частицы. Траектория молекулы также изломана, как и линия, представленная на рис. 7.1. Для количественной характеристики интенсивности столкновений молекул используется четыре параметра: 1. Эффективное сечение молекулы 2. Средняя длина свободного пробега молекул 3. Среднее время между столкновениями 4. Средняя частота столкновений
Все эти параметры связаны между собой. Эффективное сечение молекул
Обычно, при рассмотрении столкновений одну частицу выделяют как движущуюся, а все остальные считаются неподвижными частицами-мишенями (рис. 17.1).
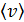 относительно стенок сосуда, а средней относительной скоростью относительно стенок сосуда, а средней относительной скоростью 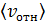 двух произвольно взятых молекул. Прямое вычисление этой скорости с помощью распределения Максвелла дает результат: двух произвольно взятых молекул. Прямое вычисление этой скорости с помощью распределения Максвелла дает результат:
Вероятность того, что движущаяся частица попадет в одну из частиц-мишеней при прохождении слоя толщиной
Коэффициент пропорциональности При столкновении молекула может изменить направление своего движения, т.е. рассеяться. Может поглотиться, диссоциировать молекулу или ионизировать атом, с которыми она сталкивается. В соответствии с этим говорят об эффективных сечениях рассеяния, поглощения, диссоциации, ионизации и пр. В ядерной физике и физике элементарных частиц так же широко используется понятие эффективного сечения частицы по отношению к какому-либо процессу. Сильная зависимость
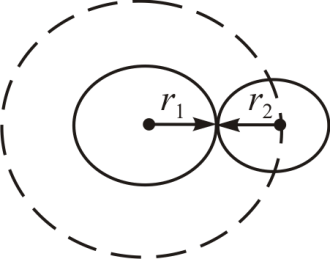 Минимальное расстояние, на которое сближаются центры двух тождественных молекул при столкновении, называются эффективным диаметром молекулы Минимальное расстояние, на которое сближаются центры двух тождественных молекул при столкновении, называются эффективным диаметром молекулы 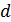 (рис. 17.2.). Площадь ограниченная пунктирной окружностью на рисунке равна эффективному сечению молекулы (рис. 17.2.). Площадь ограниченная пунктирной окружностью на рисунке равна эффективному сечению молекулы 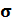 : :
Если сталкивающиеся молекулы не тождественны, то
Параметр Роль притяжения проявляется при малых относительных скоростях движения молекул, т.е. при низких температурах. Эксперименты обнаруживают некоторое уменьшение эффективного сечения молекул с ростом температуры. В своей теории Сёзерленд получил формулу, носящую его имя, для среднего эффективного сечения молекулы реального газа
где, Средняя длина свободного пробега молекулы
Продолжим анализ формулы (17.1). Вероятность столкновения, как можно заметить, растет пропорционально пройденному молекулой пути Согласно (17.1) получаем равенство
из которого следует, что
Формула (17.5) справедлива, если система состоит только из тождественных молекул. Если молекулы в системе разные, то надо учесть вероятность столкновений, как тождественных молекул, так и разных молекул друг с другом. В этом случае
Здесь Кинематические параметры
Из определения параметров
Тогда средняя частота столкновений будет равна
Сделаем количественную оценку четырех кинематических параметров на примере молекулярного азота при нормальных условиях, т.е. в приближении идеального газа:
Здесь использовалось число Лошмидта
После рассмотрения характеристик столкновений молекул нашей ближайшей задачей будет установление связи между макроскопическими коэффициентами переноса в идеальном газе с его кинематическими параметрами.
17.2. Обобщенное уравнение переноса
Решение поставленной задачи будет базироваться на выводе обобщенного уравнения переноса. Используемый для этой цели метод средней длины свободного пробега является оценочным. Главное достоинство такого подхода состоит в его простоте и акценте на физической сущности явления. Ожидаемые результаты могут отличаться от точных числовыми коэффициентами. Точные решения следуют из кинетического уравнения Больцмана.
Вывод обобщенного уравнения процесса
Описание системы Рассматриваемая система – идеальный газ в слабо неравновесном состоянии.
Актуальные свойства модели процесса
• При наличии градиента • Перенос
• Функциональная зависимость G(x) не известна. • Чтобы восполнить этот пробел воспользуемся разложением Постановка задачи Требуется получить обобщенное уравнение переноса на основе микроскопических представлений. Вывод уравнения
• Величину малого параметра • Изобразим встречные молекулярные потоки на схематическом рисунке (рис. 17.3), где ось
Рис.17.3.
• Величина
• Тогда, плотность потока
Плотность потока
• Суммарная плотность потока в положительном направлении оси Х :
• При
Это и есть обобщенное уравнение переноса.
17.3. Элементарная кинетическая теория теплопроводности, самодиффузии и вязкости плотных идеальных газов Получим уравнение теплопроводности, самодиффузии и вязкости, исходя из обобщенного уравнения переноса (17.9). 1. Пусть переносимым молекулярным свойством является внутренняя энергия идеального газа, приходящегося на одну молекулу:
В этом случае обобщенное уравнение переноса переходит в уравнение теплопроводности
Выражение перед
Формула (17.7) выражает зависимость теплопроводности от микроскопических параметров В этом легко убедиться. При фиксированной температуре в выражении (17.11) от концентрации частиц зависят два множителя: Для газов при нормальных условиях 2. Пусть переносимое молекулярное свойство – концентрация «меченных» атомов, приходящаяся на одну молекулу фона:
В этом случае обобщенное уравнение переноса переходит в уравнение самодиффузии
Выражение перед
Как видим 3. Пусть переносимое молекулярное свойство - это импульс упорядоченного движения одной молекулы:
В этом случае обобщены уравнение переноса переходит в уравнение внутреннего трения или вязкости
Следовательно, коэффициент вязкости
Функциональная зависимость Вы без особого труда самостоятельно можете получить формулы, выражающие один коэффициент переноса через любой другой. Это дает возможность из исследования только какого-то одного явления переноса получить информацию о других процессах переноса. Экспериментальные измерения макроскопических коэффициентов переноса и полученные для них выражения в рамках кинетической теории (17.10), (17.13) и (17.15) позволяют определить такие микроскопические параметры как Физическая сущность таких явлений как теплопроводность и вязкость состоит в том, что в процессе столкновений молекул энергия теплового движения (теплопроводность) и импульс упорядоченного движения (вязкость) передаются от частицы к частице, от слоя к слою как эстафетная палочка. Несмотря на то, что частицы пребывают в хаотическом движении и беспорядочной толкотне, возникает упорядоченное движение определенного молекулярного свойства – поток энергии или поток импульса. 17.4. Явления переноса в ультраразреженных газах Состояние разреженного газа называют вакуумом . Степень разрежения характеризуют тремя параметрами:
Таблица. 17.1.
Для описания явлений переноса наиболее «прозрачным» является случай ультраразреженного газа. Поскольку в этих условиях столкновения между молекулами практически отсутствуют, то и «эстафетный» механизм передачи молекулярных свойств не работает. Молекулы по прямым линиям летят от одной стенки сосуда к другой и обмениваются с ними, например, энергией (это уже не теплопроводность, а теплопередача) или импульсом упорядоченного движения (трение при малых давлениях). Механизмы переноса можно легко смоделировать, используя уравнение эффузии. Одной из особенностей высокого вакуума является невозможность возникновения в нем конвекционных потоков. Наиболее трудным для теории является случай среднего вакуума, когда
Трение и теплопроводность ультраразреженных газов Независимость коэффициентов внутреннего трения и теплопроводности от давления газа, обоснованная нами в 17.3. имеет место при таких давлениях, когда Аналогичное заключение можно сделать и по поводу теплопередачи. Молекула как пчела, несущая нектар, летит от горячей стенки к холодной и передает ей свою кинетическую энергию. После чего она «холодная и голодная» возвращается к горячей стенке за новой порцией энергии. Механизм выравнивания температуры именно таков. Количество перенесенной молекулами энергии пропорционально числу ударов о стенки, т.е. концентрации или давлению газа. Коэффициент теплопередачи растет пропорционально давлению.
Тепловая и изотермическая эффузия
Интересные явления наблюдаются в сосудах с газом, сообщающихся через очень тонкую пористую перегородку. Размеры пор могут быть столь малыми ( Схема 17.4.1.
Число частиц в эффузионном потоке через пористую перегородку в одном направлении равно
здесь произведение всех констант обозначено в равновесном состоянии равен нулю. В случае тепловой эффузии, когда молекулы тождественны, равновесному состоянию согласно (17.15) соответствует равенство
или
Очевидно, что в той половинке сосуда, где температура больше установится и более высокое давление. Это произойдет за счет увеличения концентрации частиц в «теплом» отсеке. Особенно наглядно это проявляется, если первоначально давления в разных отсеках были равны В случае изотермической эффузии в начальный момент времени
Если
 Рассмотренные виды эффузии имеют практическое значение. Изотермическая эффузия лежит в основе одного из методов разделения изотопов. Тепловая эффузия играет важную роль в явлениях природы, обеспечивая обмен воздуха в почве, необходимый для нормальной жизни растений. Дадим пояснения этому практически значимому феномену. Рассмотренные виды эффузии имеют практическое значение. Изотермическая эффузия лежит в основе одного из методов разделения изотопов. Тепловая эффузия играет важную роль в явлениях природы, обеспечивая обмен воздуха в почве, необходимый для нормальной жизни растений. Дадим пояснения этому практически значимому феномену.
Летом в дневное время суток поверхность земли нагревается солнечным излучением. Поэтому воздух из более глубоких и менее нагретых слоев почвы выходит по капиллярам природного происхождения наверх и разносится ветром. Ночью верхний слой земли охлаждается и возникает обратный поток воздуха с поверхности в более глубокие слои почвы. Таким образом, осуществляется суточная циркуляция воздуха в плодородных слоях земли. В заключение темы отметим, что рассмотренные нами процессы переноса в газах не исчерпывают всех явлений такого рода. Например, в плотных газах мы обошли вниманием взаимную диффузию различных газов, а также термодиффузию. Остались в запасниках и некоторые явления в ультраразреженных газах, например, такие как течение Кнудсена, тепловое скольжение, радиометрический эффект. Вот уж воистину, чем больше узнаешь, тем больше граница с непознанным…
Контрольные вопросы
1. Назовите параметры, определяющие интенсивность столкновений молекул друг с другом. 2. Как определяется вероятность столкновения молекулы с другими частицами? 3. Что характеризует эффективное сечение молекулы? 4. Какого рода столкновения молекул определяют явления переноса? 5. Как определяется 6. Как определяется 7. Дайте определение средней длины свободного пробега молекул. 8. Назовите исходные положения, необходимые для вывода обобщенного уравнения переноса. Запишите это уравнение. 9. На основе обобщенного уравнения переноса получите выражение для а) теплопроводности; б) вязкости; в) коэффициента диффузии. 10. Раскройте физическую (микроскопическую) сущность явлений переноса. 11. Какие существуют градации состояний разреженного газа? 12. Назовите явления переноса в ультраразреженном газе, которые были рассмотрены на этой лекции? Какие эффекты и количественные соотношения для них характерны?
ЛЕКЦИЯ 18
АТМОСФЕРЫ ПЛАНЕТ
18.1. Атмосфера как открытая система и как открытая книга
Для молекулярной физики атмосферы планет представляют уникальные объекты исследования. Это гигантские газовые тела, не имеющие материальных границ и находящиеся в неоднородных гравитационных полях и потоках солнечного и галактического излучения. Атмосферы планет являются открытыми и существенно неравновесными системами. Температура в атмосфере планеты сложным образом зависит от координат. В атмосфере происходят разнообразные физические процессы и фотохимические реакции. Поэтому к планетной атмосфере в целом распределение Больцмана не применимо, так как при его выводе предполагалось, что газ находится в состоянии термодинамического равновесия с температурой, постоянной по всему объему газовой среды. Исходя из представления о локальном равновесии (см.13.1), можно считать, что распределение Максвелла не теряет своей справедливости в квазиравновесных подсистемах. Вследствие распределения молекул по скоростям в атмосферах планет всегда имеется некоторое количество частиц, скорость которых больше второй космической скорости, зависящей от массы планеты. Так для Земли Вблизи планеты относительная концентрация убегающих молекул в этом потоке очень мала. По мере удаления от планеты их относительная концентрация возрастает. На бесконечности все молекулы являются убегающими. В конце концов, планета должна потерять свою атмосферу. Время Изучение атмосфер планет в настоящее время ведется по трем направлениям. Популярное:
|
Последнее изменение этой страницы: 2016-03-17; Просмотров: 1211; Нарушение авторского права страницы