Геометрическая интерпретация тензоров
Го и 2-го рангов.
Тензор 1-го ранга обычно интерпретируется как вектор, т.е. как направленный отрезок. Возможно и другое истолкование тензора 1-го ранга. Рассмотрим произвольную плоскость в пространстве, не проходящую через начало координат. Как известно из курса линейной алгебры, общее уравнение плоскости имеет вид:  .
.
Поскольку плоскость не проходит через начало координат, то свободный член 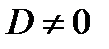 . Разделив обе части уравнения на
. Разделив обе части уравнения на 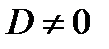 , преобразуем его к виду:
, преобразуем его к виду:
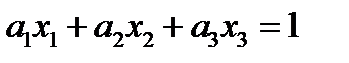 (92)
(92)
где 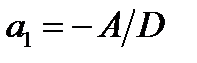 ,
,  ,
, 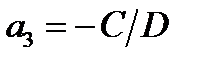 , а координаты
, а координаты 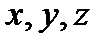 обозначены через
обозначены через 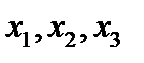 . Уравнение (92) сокращенно записывается так:
. Уравнение (92) сокращенно записывается так: 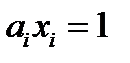 (93)
(93)
Перейдем теперь в новую систему координат. Координаты 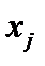 при этом преобразуются по формулам (27), (29). Подставив в (93) формулу (29), получим в новой системе
при этом преобразуются по формулам (27), (29). Подставив в (93) формулу (29), получим в новой системе 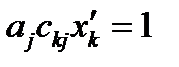 или
или 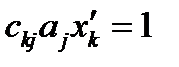 . Обозначив
. Обозначив  (94)
(94)
получим, что в новой системе координат уравнение плоскости имеет вид: 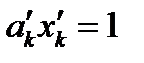 (95)
(95)
Из (94) следует, что коэффициенты уравнения плоскости преобразуются так же, как компоненты тензора 1-ого ранга. Таким образом, тензор 1-го ранга может быть интерпретирован геометрически как плоскость.
Все вышесказанное наводит на мысль, что тензор 2-го ранга также должен иметь геометрическое истолкование. Очевидно, в виде более сложной поверхности, чем плоскость.
Рассмотрим центральную поверхность 2-го порядка, т.е. поверхность, имеющую центр симметрии. Если центр поверхности находится в начале координат, то уравнение поверхности можно записать в виде:
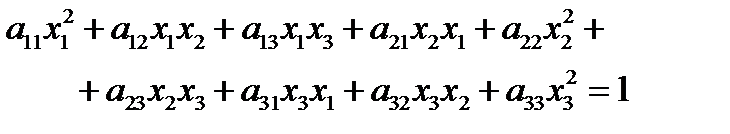 (96)
(96)
Здесь коэффициенты  . Эта поверхность в общем случае будет эллипсоидом или гиперболоидом. Уравнение (96) сокращенно можно записать так:
. Эта поверхность в общем случае будет эллипсоидом или гиперболоидом. Уравнение (96) сокращенно можно записать так:
 (97)
(97)
При переходе к новой системе координат координаты 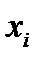 ,
, 
 преобразуются по формулам (27), (29). Поэтому в новой системе координат получим:
преобразуются по формулам (27), (29). Поэтому в новой системе координат получим: 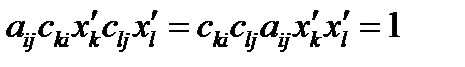 .
.
Обозначив 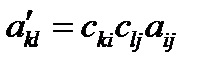 , (98)
, (98)
запишем 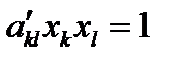 (99)
(99)
Это уравнение той же поверхности в новой системе координат с новыми коэффициентами 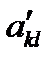 . Из (98) видно, что коэффициенты поверхности 2-го порядка преобразуются подобно компонентам симметричного тензора 2-го ранга. Таким образом, законы преобразования симметричного тензора 2-го ранга совпадают с законами преобразования поверхностей 2-го порядка. Чтобы найти, как преобразуются компоненты такого тензора, достаточно рассмотреть преобразование соответствующей поверхности 2-го порядка. По этой причине поверхность (97) называется характеристической поверхностью 2-го порядка для тензора.
. Из (98) видно, что коэффициенты поверхности 2-го порядка преобразуются подобно компонентам симметричного тензора 2-го ранга. Таким образом, законы преобразования симметричного тензора 2-го ранга совпадают с законами преобразования поверхностей 2-го порядка. Чтобы найти, как преобразуются компоненты такого тензора, достаточно рассмотреть преобразование соответствующей поверхности 2-го порядка. По этой причине поверхность (97) называется характеристической поверхностью 2-го порядка для тензора.
Тензоры высших порядков.
Будем исходить из формулы (51). Мы уже сделали шаг в направлении ее обобщения (формула (58)) и пришли к понятию тензора 2-ого ранга. Сделаем дальнейшее обобщение.
Пусть всякому направлению в пространстве  сопоставляется не вектор (тензор 1-ого ранга), а тензор 2-ого ранга посредством линейного и однородного относительно направляющих косинусов соотношения. Геометрический объект с таким свойством называется тензором 3-его ранга. Обобщение можно продолжать и дальше. Тогда для любого направления в пространстве тензору ранга
сопоставляется не вектор (тензор 1-ого ранга), а тензор 2-ого ранга посредством линейного и однородного относительно направляющих косинусов соотношения. Геометрический объект с таким свойством называется тензором 3-его ранга. Обобщение можно продолжать и дальше. Тогда для любого направления в пространстве тензору ранга 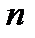 можно поставить в соответствие тензор ранга
можно поставить в соответствие тензор ранга  посредством линейного и однородного относительно направляющих косинусов соотношения. Рассмотрим тензор 3-его ранга. Он обозначается
посредством линейного и однородного относительно направляющих косинусов соотношения. Рассмотрим тензор 3-его ранга. Он обозначается 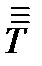 . Его проекцию на произвольное направление
. Его проекцию на произвольное направление 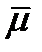 обозначим
обозначим 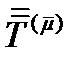 – это тензор 2-ого ранга. Обобщая (51) и (58), запишем:
– это тензор 2-ого ранга. Обобщая (51) и (58), запишем:
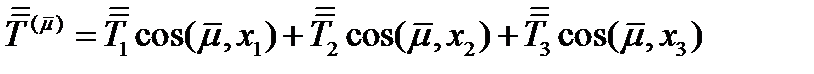 (100)
(100)
Совмещая поочередно направление 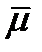 с направлениями осей координат, легко показать, что тензоры
с направлениями осей координат, легко показать, что тензоры 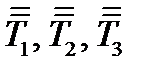 – это проекции тензора 3-го ранга
– это проекции тензора 3-го ранга 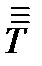 на оси координат. Таким образом, тензор 3-го ранга определяется тремя тензорами 2-ого ранга – своими проекциями. Компоненты этих проекций обозначим
на оси координат. Таким образом, тензор 3-го ранга определяется тремя тензорами 2-ого ранга – своими проекциями. Компоненты этих проекций обозначим 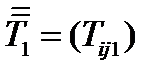 ,
,  ,
,  . Всего их будет 27, обозначаются они
. Всего их будет 27, обозначаются они  с помощью трех индексов и называются компонентами тензора
с помощью трех индексов и называются компонентами тензора 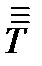 в рассматриваемом базисе. Выясним, как преобразуются компоненты тензора 3-его ранга при переходе к другой системе координат.
в рассматриваемом базисе. Выясним, как преобразуются компоненты тензора 3-его ранга при переходе к другой системе координат.
Совместим направление 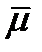 с направлением оси
с направлением оси 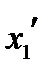 новой системы координат. Проекцию тензора
новой системы координат. Проекцию тензора 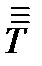 на это направление обозначим
на это направление обозначим 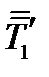 – это тензор 2-ого ранга:
– это тензор 2-ого ранга:
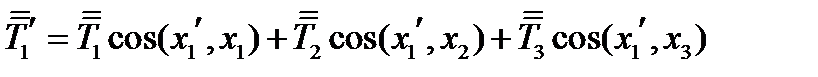 (101)
(101)
Совместив направление 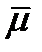 последовательно с направлениями осей
последовательно с направлениями осей  и
и 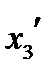 , получим проекции на эти оси:
, получим проекции на эти оси:
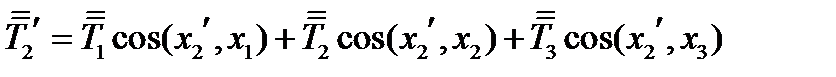 (102)
(102)
 (103)
(103)
Используя матрицу перехода  , перепишем эти формулы так:
, перепишем эти формулы так:
 (104а)
(104а)
 (104б)
(104б)
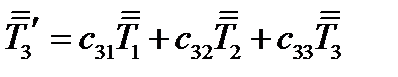 (104в)
(104в)
В новой системе тензор 3-его ранга 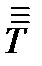 также определяется тремя своими проекциями
также определяется тремя своими проекциями  . Их компоненты
. Их компоненты 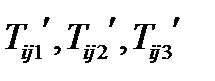 – это компоненты того же тензора в новой системе координат. Найдем формулы преобразования компонент тензора
– это компоненты того же тензора в новой системе координат. Найдем формулы преобразования компонент тензора 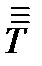 . Формула (104а) покомпонентно в новом базисе запишется так:
. Формула (104а) покомпонентно в новом базисе запишется так:
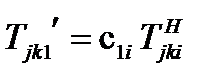 (105)
(105)
где через 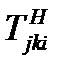 обозначены компоненты тензора
обозначены компоненты тензора 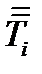 в новом базисе. Выразим компоненты
в новом базисе. Выразим компоненты 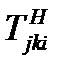 через компоненты тензора
через компоненты тензора 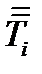 в старом базисе по формулам перехода (70) для тензоров 2-ого ранга:
в старом базисе по формулам перехода (70) для тензоров 2-ого ранга:
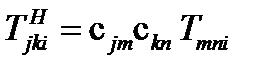 (106)
(106)
Тогда 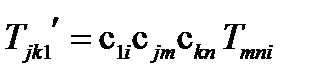 .
.
Аналогично, из формул (104б, в) получим:
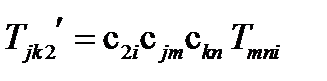 ,
,  (107)
(107)
Объединив все три формулы в одну, будем иметь:
 (108)
(108)
Это и есть формула перехода от старой системы координат к новой для тензора 3-его ранга. Получим обратную формулу. Для этого умножим обе части (108) на 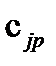 :
:
 .
.
Теперь умножим обе части на 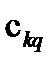 :
: 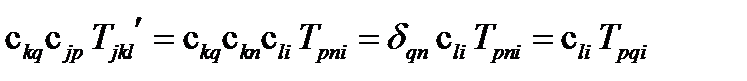 .
.
Наконец, умножим на 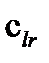 :
:
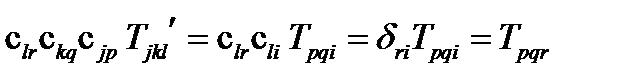 ,
,
т.е. 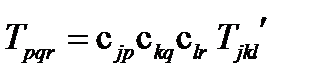 (109)
(109)
Это и есть искомая формула преобразования от новой системы координат к старой.
Формулы (108) и (109) можно положить в основу нового определения тензора 3-его ранга. В любой прямоугольной системе координат тензор 3-его ранга определяется двадцатью семью компонентами, которые при преобразовании координат преобразуются по формулам (108), (109). Теперь можно сделать обобщение на тензоры произвольного ранга. В любой прямоугольной декартовой системе координат тензор ранга 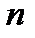 определяется
определяется 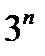 компонентами, которые при преобразовании координат преобразуются по формулам:
компонентами, которые при преобразовании координат преобразуются по формулам:
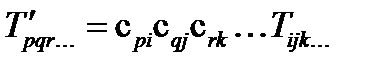 ,
, 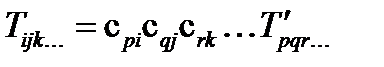 (110)
(110)
Проекция тензора 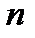 -го ранга на произвольное направление является тензором ранга
-го ранга на произвольное направление является тензором ранга  .
.
Операции с тензорами.
Рассмотрим алгебраические операции с тензорами, с помощью которых по тензорам можно составлять новые тензоры. Эти операции инвариантны в том смысле, что в результате получается вполне определенный тензор, не зависящий от того, в какой системе координат они выполняются. Тензорные операции отражают те операции над геометрическими и физическими объектами, заданными посредством тензоров, которые имеют геометрический или физический смысл и совершаются независимо от выбора координатной системы.
Умножение на скаляр. Умножение всех компонент тензора на один и тот же скаляр дает тензор того же ранга, который называется произведением тензора на скаляр. Например,  или в символической бескоординатной записи
или в символической бескоординатной записи  .
.
Сложение тензоров. Сложение соответствующих компонент двух тензоров одинакового ранга дает третий тензор того же ранга. Например,  или
или 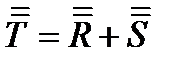 . Подчеркнем, что складывать можно только тензоры одинаковых рангов.
. Подчеркнем, что складывать можно только тензоры одинаковых рангов.
Умножение тензоров. Совокупность всех произведений, содержащих по одной компоненте каждого из двух тензоров, образует тензор – произведение первых двух тензоров. Ранг произведения равен сумме рангов сомножителей. Например, произведение 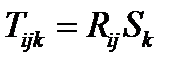 тензора 2-ого ранга и вектора
тензора 2-ого ранга и вектора 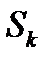 представляет собой тензор 3-его ранга. В частности, произведение двух тензоров 1-ого ранга
представляет собой тензор 3-его ранга. В частности, произведение двух тензоров 1-ого ранга  и
и 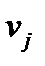 является тензором 2-ого ранга
является тензором 2-ого ранга  и называется диадным произведением векторов
и называется диадным произведением векторов  и
и 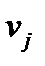 . В символической бескоординатной записи это будет выглядеть так
. В символической бескоординатной записи это будет выглядеть так 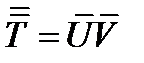 . Диадное произведение называется еще иначе неопределенным произведением векторов. Особенностью его является то, что оно не обладает свойствами коммутативности:
. Диадное произведение называется еще иначе неопределенным произведением векторов. Особенностью его является то, что оно не обладает свойствами коммутативности: 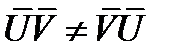 . Точнее, при перестановке сомножителей получается транспонированный тензор, т.е.
. Точнее, при перестановке сомножителей получается транспонированный тензор, т.е.  или
или 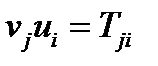 .
.
Свертывание. Приравнивание двух буквенных индексов тензора ранга 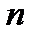 дает тензор ранга
дает тензор ранга 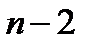 и называется свертыванием исходного тензора по этим индексам. Например, тензор 3-его ранга
и называется свертыванием исходного тензора по этим индексам. Например, тензор 3-его ранга  можно свернуть по парам индексов
можно свернуть по парам индексов 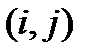 ,
, 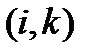 ,
, 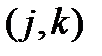 . В результате получатся тензоры 1-ого ранга
. В результате получатся тензоры 1-ого ранга 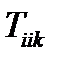 ,
,  ,
,  . Как обычно, по паре повторяющихся индексов должно производиться суммирование. Поэтому:
. Как обычно, по паре повторяющихся индексов должно производиться суммирование. Поэтому:
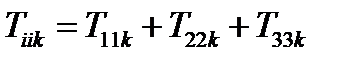 ,
,  ,
, 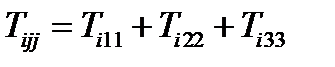 (111)
(111)
Свертывание тензора 2-ого ранга  дает скаляр:
дает скаляр:
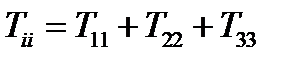 (112)
(112)
который называется следом тензора  . В бескоординатных обозначениях след тензора
. В бескоординатных обозначениях след тензора  записывается в виде
записывается в виде 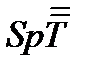 или
или  . Такое обозначение проистекает от немецкого слова Spur или английского Trace. В переводе и то, и другое означает – след. Известное из курса векторной алгебры скалярное произведение векторов
. Такое обозначение проистекает от немецкого слова Spur или английского Trace. В переводе и то, и другое означает – след. Известное из курса векторной алгебры скалярное произведение векторов 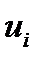 и
и  можно рассматривать как след диадного произведения
можно рассматривать как след диадного произведения  , т.е.
, т.е. 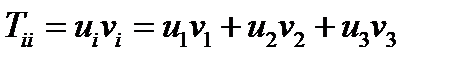 .
.
Образование целых положительных степеней тензора 2-ого ранга является еще одним примером свертывания. Квадрат тензора  определяется как тензор
определяется как тензор 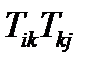 , куб – как тензор
, куб – как тензор 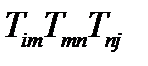 , четвертая степень – как
, четвертая степень – как  , и т.д. Каждая степень тензора 2-ого ранга является тензором того же ранга. В бескоординатном обозначении степени тензора
, и т.д. Каждая степень тензора 2-ого ранга является тензором того же ранга. В бескоординатном обозначении степени тензора  записываются в виде
записываются в виде 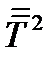 ,
, 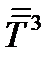 и т.д.
и т.д.
Приведем еще несколько примеров бескоординатной записи: 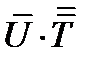 для вектора
для вектора  ;
; 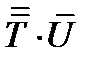 для вектора
для вектора 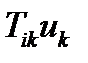 ;
; 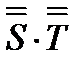 для тензора второго ранга
для тензора второго ранга  ;
; 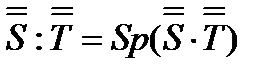 для скаляра
для скаляра 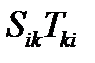 .
.
Перестановка индексов или образование изомеров. Перестановка двух индексов тензора дает другой тензор того же ранга, называемый изомером первого тензора. Тензор 2-го ранга  имеет единственный изомер
имеет единственный изомер  , который ранее мы называли транспонированным тензором. Тензор 3-его ранга
, который ранее мы называли транспонированным тензором. Тензор 3-его ранга 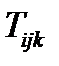 имеет изомеры
имеет изомеры 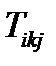 ,
, 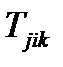 ,
,  ,
, 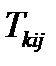 ,
, 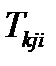 .
.
Тензор называется симметричным относительно двух индексов, если он равен своему изомеру, полученному при перестановке этих индексов. Например, если тензор 3-его ранга 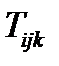 симметричен по индексам
симметричен по индексам 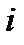 и
и 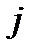 , то
, то  . Если же тензор равен своему изомеру с обратным знаком, то он антисимметричен относительно этих индексов. Например, если тензор
. Если же тензор равен своему изомеру с обратным знаком, то он антисимметричен относительно этих индексов. Например, если тензор  антисимметричен по индексам
антисимметричен по индексам 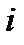 и
и  , то
, то 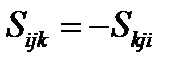 .
.
Компоненты антисимметричного тензора с одинаковыми значениями индексов, по которым тензор антисимметричен, равны нулю. Так, у упомянутого антисимметричного тензора  компоненты
компоненты 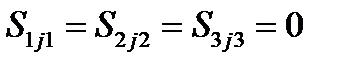 . Легко убедиться, что эти определения включают в себя определения, введенные в параграфе 12. Тензор называется полностью антисимметричным или просто антисимметричным, если при перестановке любых двух его индексов у любой его компоненты она меняет знак. Заметим, что в рассматриваемом нами трехмерном пространстве невозможен полностью антисимметричный тензор более чем третьего ранга. Точнее, такой тензор всегда имеет лишь нулевые компоненты. В самом деле, наличие двух одинаковых индексов обращает компоненту такого антисимметричного тензора в нуль. Между тем, его компоненты всегда имеют, по меньшей мере, два одинаковых индекса, т.к. индексов у них более трех, а принимать они могут лишь значения 1, 2, 3. Следовательно, все компоненты такого тензора равны нулю.
. Легко убедиться, что эти определения включают в себя определения, введенные в параграфе 12. Тензор называется полностью антисимметричным или просто антисимметричным, если при перестановке любых двух его индексов у любой его компоненты она меняет знак. Заметим, что в рассматриваемом нами трехмерном пространстве невозможен полностью антисимметричный тензор более чем третьего ранга. Точнее, такой тензор всегда имеет лишь нулевые компоненты. В самом деле, наличие двух одинаковых индексов обращает компоненту такого антисимметричного тензора в нуль. Между тем, его компоненты всегда имеют, по меньшей мере, два одинаковых индекса, т.к. индексов у них более трех, а принимать они могут лишь значения 1, 2, 3. Следовательно, все компоненты такого тензора равны нулю.
Часто применяется следующее рассуждение. Если тензор 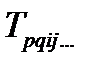 симметричен, а тензор
симметричен, а тензор 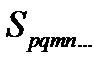 антисимметричен по индексам
антисимметричен по индексам 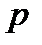 и
и 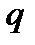 , то их свертка
, то их свертка  . В самом деле, сумма по немым индексам
. В самом деле, сумма по немым индексам 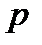 и
и 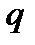 содержит, например, слагаемое с
содержит, например, слагаемое с 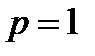 ,
, 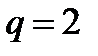 , а также слагаемое с
, а также слагаемое с 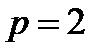 ,
, 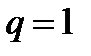 . Сумма этих двух слагаемых равна нулю, т.к.
. Сумма этих двух слагаемых равна нулю, т.к. 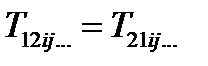 ,
, 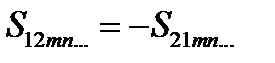 . Кроме того,
. Кроме того, 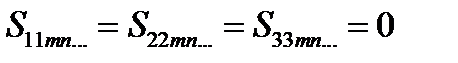 . Используя это рассуждение, можно установить следующее тождество для произвольных тензоров 2-ого ранга:
. Используя это рассуждение, можно установить следующее тождество для произвольных тензоров 2-ого ранга:
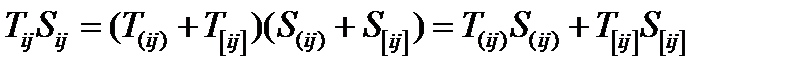 , (113)
, (113)
где 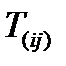 – симметричная,
– симметричная,  – антисимметричная части тензора
– антисимметричная части тензора  . Также и для тензора
. Также и для тензора 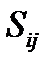 .
.
Популярное:

