Симметричного тензора 2-го ранга.
При определении тензора 2-го ранга в параграфе 9 мы исходили из того, что каждому направлению  в пространстве с помощью тензора
в пространстве с помощью тензора 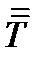 ставится в соответствие вектор
ставится в соответствие вектор  . Проекция этого вектора на то же направление:
. Проекция этого вектора на то же направление:
 (217)
(217)
называется нормальной составляющей тензора  в направлении
в направлении  . Если единичный вектор
. Если единичный вектор  совпадает с ортом какой-либо координатной оси, например,
совпадает с ортом какой-либо координатной оси, например,  , то компоненты вектора
, то компоненты вектора  будут равны:
будут равны:  ,
,  , и тогда нормальная составляющая (217) окажется просто диагональной компонентой тензора
, и тогда нормальная составляющая (217) окажется просто диагональной компонентой тензора  . Аналогично две другие диагональные компоненты тензора
. Аналогично две другие диагональные компоненты тензора  и
и 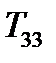 являются нормальными составляющими в направлении координатных осей
являются нормальными составляющими в направлении координатных осей  и
и  .
.
В системе координат, построенной на главных осях тензора, формула для вычисления его нормальной составляющей принимает простой вид. Считая, что  – компоненты единичного вектора
– компоненты единичного вектора  относительно главных осей тензора, получим:
относительно главных осей тензора, получим:
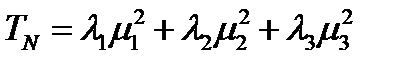 (218)
(218)
Если, в частности, два главных значения тензора совпадают  , то его нормальная составляющая зависит только от компоненты
, то его нормальная составляющая зависит только от компоненты  :
:
 (219)
(219)
Наконец, при совпадении всех трех главных значений тензора  нормальная составляющая
нормальная составляющая  .
.
Нормальные составляющие часто встречаются в кристаллофизике, и поэтому важное практическое значение приобретает вопрос, в каком направлении нормальная составляющая данного тензора принимает экстремальное значения. Математическая формулировка этой задачи такова: найти значения  , при которых функция (217) достигает экстремума при дополнительном условии
, при которых функция (217) достигает экстремума при дополнительном условии  . Это типичная задача на условный экстремум и решается она методом неопределенных множителей Лагранжа. Составляется функция Лагранжа:
. Это типичная задача на условный экстремум и решается она методом неопределенных множителей Лагранжа. Составляется функция Лагранжа:
 (220)
(220)
с неопределенным пока множителем  и ищется ее безусловный экстремум, т.е. приравниваются к нулю ее частные производные:
и ищется ее безусловный экстремум, т.е. приравниваются к нулю ее частные производные:  ,
,  . Чтобы найти производные, подставим в (220) выражение (217) и после небольших преобразований получим:
. Чтобы найти производные, подставим в (220) выражение (217) и после небольших преобразований получим:  (221)
(221)
Теперь дифференцируем:
 .
.
Производная от компоненты  по
по  равна
равна  . Аналогично,
. Аналогично,  . Тогда:
. Тогда:
 Переобозначив в первом слагаемом немой индекс
Переобозначив в первом слагаемом немой индекс 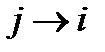 , и используя симметрию тензора, получим окончательно:
, и используя симметрию тензора, получим окончательно:  , или
, или
 (222)
(222)
Но это не что иное, как уравнение (158), определяющее главные направления тензора, а  , следовательно, главное значение. Таким образом, нормальная составляющая тензора достигает экстремальных значений на главных направлениях этого тензора. Чтобы найти, чему равняются экстремальные значения нормальной составляющей, умножим (222) на
, следовательно, главное значение. Таким образом, нормальная составляющая тензора достигает экстремальных значений на главных направлениях этого тензора. Чтобы найти, чему равняются экстремальные значения нормальной составляющей, умножим (222) на  :
:
 , (223)
, (223)
т.е. экстремальные значения нормальной составляющей равны соответствующим главным значениям тензора.
Из доказанного следует, что если все главные значения тензора положительны (отрицательны), то и все его нормальные составляющие обладают этим свойством. Если же среди главных значений тензора имеются и положительные и отрицательные, нормальная составляющая тензора также принимает и положительные, и отрицательные значения. Будучи непрерывной функцией направления, она при этом на некотором направлении должна обращаться в нуль.
Перейдем к рассмотрению тангенциальных (касательных) составляющих симметричного тензора 2-го ранга. Пусть  и
и  – взаимно перпендикулярные единичные векторы, т.е.
– взаимно перпендикулярные единичные векторы, т.е.
 ,
,  ,
,  (224)
(224)
Определение. Тангенциальной составляющей тензора 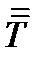 в направлениях
в направлениях  и
и  называется число:
называется число:
 (225)
(225)
Так как тензор 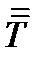 симметричен, направления
симметричен, направления  и
и  в этом определении равноправны и взаимозаменяемы.
в этом определении равноправны и взаимозаменяемы.
Если, например, вектор  совпадает с базисным вектором
совпадает с базисным вектором  , а вектор
, а вектор  – с базисным вектором
– с базисным вектором  , то
, то  ;
;  . Подставив в (225), получим:
. Подставив в (225), получим:  , т.е. компонента тензора
, т.е. компонента тензора  является его тангенциальной составляющей в направлениях
является его тангенциальной составляющей в направлениях  и
и  . Аналогично получаем, что остальные две недиагональные компоненты тензора
. Аналогично получаем, что остальные две недиагональные компоненты тензора 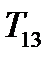 и
и  также определяют тангенциальные составляющие для пар направлений
также определяют тангенциальные составляющие для пар направлений  ,
,  и
и 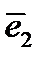 ,
, 
 Таким образом, в то время как нормальные составляющие соответствуют диагональным компонентам тензора, тангенциальные соответствуют недиагональным компонентам.
Таким образом, в то время как нормальные составляющие соответствуют диагональным компонентам тензора, тангенциальные соответствуют недиагональным компонентам.
В системе координат, построенной на главных осях, тангенциальные составляющие выражаются формулой:
 (226)
(226)
Если два главных значения совпадают  , то:
, то:
 (227)
(227)
Наконец, при совпадении всех трех главных значений  :
:
 (228)
(228)
Т.е. все тангенциальные составляющие шарового тензора равны нулю. Отсюда следует, что тангенциальные составляющие произвольного симметричного тензора совпадают с тангенциальными составляющими его девиатора.
Единичные векторы  и
и  в определении (225) однозначно определяют плоскость, ориентация которой в пространстве определяется нормальным вектором
в определении (225) однозначно определяют плоскость, ориентация которой в пространстве определяется нормальным вектором  (или
(или  ). Поэтому вектор
). Поэтому вектор  , который ставится в соответствие направлению
, который ставится в соответствие направлению  , можно разложить на две составляющие: нормальную с величиной
, можно разложить на две составляющие: нормальную с величиной  , направленную по нормали
, направленную по нормали  к плоскости, и тангенциальную или касательную, направленную вдоль плоскости и имеющую величину:
к плоскости, и тангенциальную или касательную, направленную вдоль плоскости и имеющую величину:  (рис.13). Эти две составляющие вектора
(рис.13). Эти две составляющие вектора  связаны теоремой Пифагора, поэтому квадрат тангенциальной составляющей определяется соотношением:
связаны теоремой Пифагора, поэтому квадрат тангенциальной составляющей определяется соотношением:
 (229)
(229)
Для тангенциальных составляющих экстремальная задача сложнее, чем для нормальных, но решается тем же методом. Удобнее будет перейти в систему главных осей тензора. Компоненты вектора  будут равны
будут равны  , или:
, или:
 (230)
(230)
Нормальная составляющая  в этой же системе координат определяется формулой (218). Подставив (230) и (218) в (229), вычислим квадрат тангенциальной составляющей:
в этой же системе координат определяется формулой (218). Подставив (230) и (218) в (229), вычислим квадрат тангенциальной составляющей:
 (231)
(231)
Для исследования на экстремум составляем функцию Лагранжа:
 (232)
(232)
где  – неопределенный пока множитель Лагранжа. Приравнивая к нулю производные функции Лагранжа по
– неопределенный пока множитель Лагранжа. Приравнивая к нулю производные функции Лагранжа по  и
и  , получаем систему уравнений:
, получаем систему уравнений:
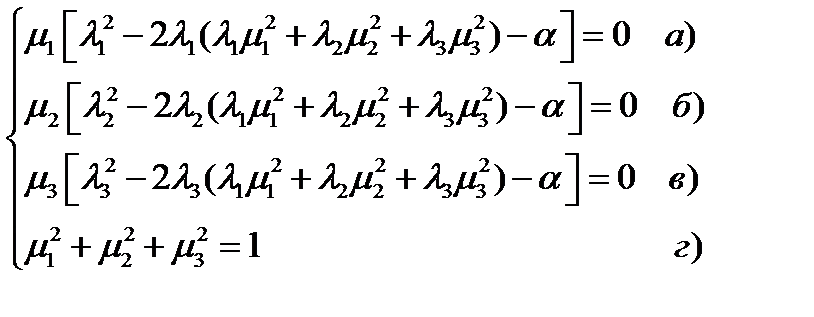 (233)
(233)
Простейшие решения этой системы и соответствующие им тангенциальные составляющие, вычисляемые по формуле (231), таковы:
 (234)
(234)
Значение тангенциальной составляющей тензора, определенное этими формулами, очевидно, является минимальным по модулю. Таким образом, как следует из (234), наименьшее значение (по абсолютной величине) тангенциальная составляющая достигает на плоскостях, определяемых главными направлениями тензора. Другие решения системы (233) имеют вид:
 (235)
(235)
Если главные значения тензора упорядочены по возрастанию, т.е.  , то максимальное по модулю значение тангенциальной составляющей определяется средней формулой и равно полуразности наибольшего и наименьшего главных значений тензора. Оно достигается на плоскости, определяемой биссектрисами углов между главными осями, соответствующими наибольшему и наименьшему главным значениям. Других решений система (233) не имеет. Подробнее решение этой системы будет рассмотрено в задачах.
, то максимальное по модулю значение тангенциальной составляющей определяется средней формулой и равно полуразности наибольшего и наименьшего главных значений тензора. Оно достигается на плоскости, определяемой биссектрисами углов между главными осями, соответствующими наибольшему и наименьшему главным значениям. Других решений система (233) не имеет. Подробнее решение этой системы будет рассмотрено в задачах.
Задачи.
Задача 27. Вывести характеристическое уравнение (163) из§23.
Решение. В §23 было получено характеристическое уравнение (161) для нахождения главных значений симметричного тензора 2-го ранга. Было сказано, что если раскрыть определитель в (161), то получится кубическое уравнение (163). Проделаем это подробно:
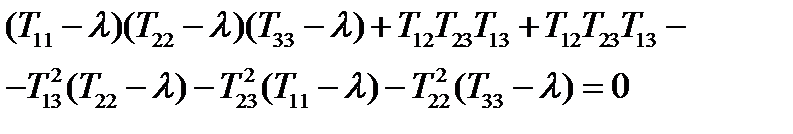 , или
, или
 , или
, или
 .
.
Обозначим:
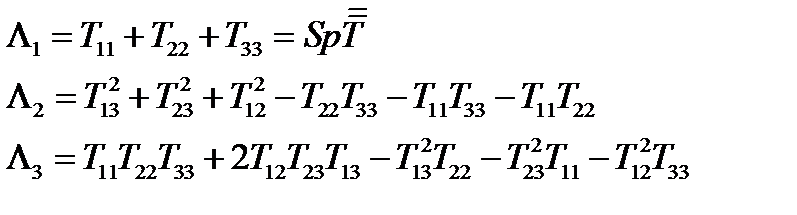 (236)
(236)
Тогда окончательно  , что совпадает с уравнением (163). Если раскрыть определители в (164)-(167), то получим формулы (236). Таким образом, главные инварианты тензора
, что совпадает с уравнением (163). Если раскрыть определители в (164)-(167), то получим формулы (236). Таким образом, главные инварианты тензора  определяются формулами (164), (165), (167) или формулами (236).
определяются формулами (164), (165), (167) или формулами (236).
Задача 28. Доказать ортогональность трех главных направлений в случае трех различных главных значений симметричного тензора 2-го ранга
Решение. В §23 утверждалось, что, если главные значения симметричного тензора  различны, то соответствующие им главные направления ортогональны. Доказательство было дано для главных направлений
различны, то соответствующие им главные направления ортогональны. Доказательство было дано для главных направлений  и
и  . Покажем здесь, что все три главных направления
. Покажем здесь, что все три главных направления  ,
,  ,
,  ортогональны между собой. Достаточно будет доказать, скажем, ортогональность главных направлений
ортогональны между собой. Достаточно будет доказать, скажем, ортогональность главных направлений  и
и  . Они удовлетворяют уравнениям:
. Они удовлетворяют уравнениям:
 ,
, 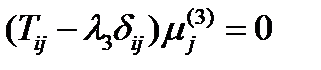 .
.
Умножим первое из них на  , второе – на
, второе – на  , и вычтем их друг из друга:
, и вычтем их друг из друга:  , или раскрывая скобки и группируя:
, или раскрывая скобки и группируя:
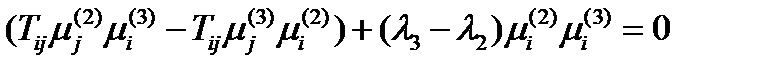 .
.
Все индексы в этом выражении немые, поэтому их можно переобозначить любыми символами. Во втором слагаемом в первых скобках заменим немые индексы так:  . Сделав это, увидим, что выражение в первых скобках обращается в нуль, и тогда
. Сделав это, увидим, что выражение в первых скобках обращается в нуль, и тогда  . Поскольку
. Поскольку  , то отсюда следует, что
, то отсюда следует, что 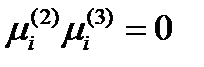 , т.е. скалярное произведение единичных главных векторов
, т.е. скалярное произведение единичных главных векторов  и
и  равно нулю. Это означает, что
равно нулю. Это означает, что  . Таким образом, мы получили, что
. Таким образом, мы получили, что 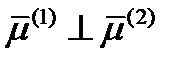 , а
, а  . Отсюда следует, что и
. Отсюда следует, что и  . Следовательно, взаимная ортогональность всех трех главных направлений доказана.
. Следовательно, взаимная ортогональность всех трех главных направлений доказана.
Задача 29. Найти главные значения и главные направления тензора  :
:  (237)
(237)
Решение: Главные значения определяются из характеристического уравнения (161), которое в данном случае имеет вид:  . Раскрывая определитель, получаем уравнение
. Раскрывая определитель, получаем уравнение  . Это кубическое уравнение. Одно его решение находится подбором:
. Это кубическое уравнение. Одно его решение находится подбором:  . Чтобы найти остальные решения, разделим кубический многочлен на
. Чтобы найти остальные решения, разделим кубический многочлен на 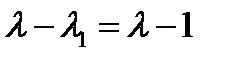 . В результате получим квадратное уравнение, корни которого
. В результате получим квадратное уравнение, корни которого  ,
,  . Чтобы найти главное направление, соответствующее
. Чтобы найти главное направление, соответствующее  , подставим его в систему уравнений (160) и получим:
, подставим его в систему уравнений (160) и получим:  .
.
Выразим из первого уравнения 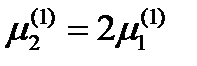 и подставим во второе уравнение. Получаем
и подставим во второе уравнение. Получаем  . Отсюда
. Отсюда  ,
,  . Чтобы найти третью компоненту
. Чтобы найти третью компоненту  , воспользуемся тем, что вектор
, воспользуемся тем, что вектор  единичный и поэтому
единичный и поэтому  . Тогда получим
. Тогда получим  . Таким образом, первое главное направление определяется вектором
. Таким образом, первое главное направление определяется вектором  .
.
Для нахождения второго главного направления, подставим  в (160):
в (160):  .
.
Имеем  ,
,  . Из условия единичности вектора
. Из условия единичности вектора  получим
получим  . Вектор второго главного направления:
. Вектор второго главного направления:  .
.
Наконец, для третьего главного направления получается система: 
Ее решение  . Теперь можно записать матрицу перехода от исходной системы координат, в которой задан тензор (237), к главной, определяемой главными направлениями:
. Теперь можно записать матрицу перехода от исходной системы координат, в которой задан тензор (237), к главной, определяемой главными направлениями:
 (238)
(238)
Каждый из полученных векторов  ,
,  ,
,  определяет два взаимно противоположных направления. Поэтому существуют две главные системы координат в зависимости от того, взят у элементов матрицы (238) верхний или нижний знак. Легко подсчитать, что если взять верхний знак в (238), то
определяет два взаимно противоположных направления. Поэтому существуют две главные системы координат в зависимости от того, взят у элементов матрицы (238) верхний или нижний знак. Легко подсчитать, что если взять верхний знак в (238), то  ; в противоположном случае
; в противоположном случае  . Таким образом, одна из главных координатных систем является левой, а вторая правой. Если ограничиться только правыми системами и считать, что исходная система координат, в которой был задан тензор (237), является правой, то в матрице (238) следует выбрать нижние знаки. После перехода в главную систему координат тензор будет иметь вид:
. Таким образом, одна из главных координатных систем является левой, а вторая правой. Если ограничиться только правыми системами и считать, что исходная система координат, в которой был задан тензор (237), является правой, то в матрице (238) следует выбрать нижние знаки. После перехода в главную систему координат тензор будет иметь вид:  .
.
Задача 30. Привести к главным осям тензор:
 (239)
(239)
Решение: Характеристическое уравнение имеет вид:  , или
, или 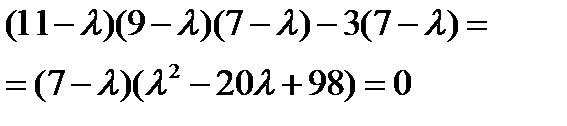 .
.
Отсюда:  ;
;  ;
; 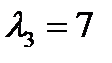 .
.
Для нахождения первого главного направления, соответствующего главному значению  , имеем систему:
, имеем систему:
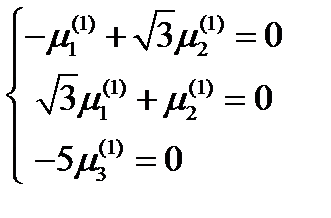
Здесь только два независимых уравнения, так как второе уравнение равно первому, умноженному на  . Поэтому находим:
. Поэтому находим:  ,
,  . Из условия единичности вектора
. Из условия единичности вектора  находим
находим 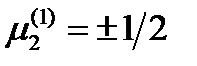 ,
, 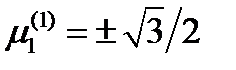 , т.е.
, т.е.  . Для второго главного направления, соответствующего
. Для второго главного направления, соответствующего  , получаем:
, получаем:  .
.
Решение системы:  ,
, 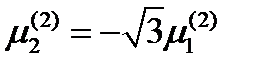 . Из условия единичности вектора
. Из условия единичности вектора  окончательно получаем:
окончательно получаем:  . Наконец, для третьего главного направления получаем систему:
. Наконец, для третьего главного направления получаем систему:  .
.
Первые два уравнения образуют систему двух однородных линейных уравнений с двумя неизвестными. Определитель ее равен 5. Поэтому она имеет только тривиальное нулевое решение  . Компонента
. Компонента  может иметь любое значение, но из требования единичности вектора
может иметь любое значение, но из требования единичности вектора  следует, что
следует, что  . Итак,
. Итак,  , т.е. третье главное направление параллельно
, т.е. третье главное направление параллельно
оси  . Матрица перехода к главным осям выглядит так:
. Матрица перехода к главным осям выглядит так:  (240)
(240)
Она определяет две главных системы координат. Чтобы выбрать из них правую, найдем определитель матрицы. Он будет равен +1, если взять нижние индексы у элементов матрицы перехода. Тензор (239) можно теперь записать в соответствии с формулой (175):
 .
.
Задача 31 . Используя построение окружности Мора привести к главным осям тензор
 (241)
(241)
Решение. По формулам (199)-(201), полученным с помощью рис. 12, находим: 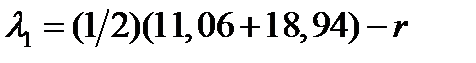 ;
;  ,
,
где  , и тогда
, и тогда 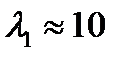 ,
,  ,
,  ,
,  ,
,  . Это означает, что для того чтобы привести тензор (242) к главным осям, нужно повернуть систему координат вокруг оси
. Это означает, что для того чтобы привести тензор (242) к главным осям, нужно повернуть систему координат вокруг оси  на угол
на угол  в направлении от оси
в направлении от оси  к
к 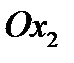 .
.
Задача 32. Доказать, что степени симметричного тензора 2-го ранга  также являются симметричными тензорами.
также являются симметричными тензорами.
Решение. Квадрат тензора определяется так:  . Переставив местами индексы
. Переставив местами индексы  и
и  , и используя симметричность исходного тензора, получим:
, и используя симметричность исходного тензора, получим:  . Куб тензора определяется так:
. Куб тензора определяется так: 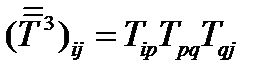 . Проделав то же самое, получим:
. Проделав то же самое, получим: 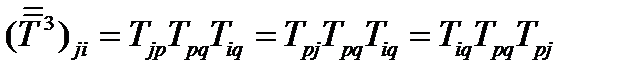 .
.
Индексы  и
и  немые. Переобозначив их
немые. Переобозначив их  ,
,  , и используя симметричность исходного тензора, получаем:
, и используя симметричность исходного тензора, получаем:  . Аналогично доказывается симметричность и любой другой степени тензора
. Аналогично доказывается симметричность и любой другой степени тензора  .
.
Задача 33. Найти главные значения тензора  и убедиться, что его главные оси совпадают с главными осями тензора
и убедиться, что его главные оси совпадают с главными осями тензора  из задачи 29.
из задачи 29.
Решение. Исходный тензор определен в (237). Его квадрат:
 (242)
(242)
Характеристическое уравнение для тензора  имеет вид:
имеет вид:
 (243)
(243)
Его корни:  ;
;  ;
;  . Главное направление для
. Главное направление для  определяется из системы:
определяется из системы:  . Решением этой системы при условии
. Решением этой системы при условии  будет вектор
будет вектор  . Для
. Для  имеем систему:
имеем систему:  . Ее решение:
. Ее решение:  . Наконец, для
. Наконец, для  имеем систему:
имеем систему:  . Ее решение:
. Ее решение:  . Видно, что главные направления
. Видно, что главные направления  и
и  одни и те же.
одни и те же.
Задача 34. Воспользовавшись тем, что тензор  и симметричный тензор
и симметричный тензор  имеют одни и те же главные значения, найти тензор
имеют одни и те же главные значения, найти тензор  , если:
, если:  (244)
(244)
Решение: Прежде всего, будем искать главные значения и главные направления тензора  . Действуя так же, как в задаче 29, найдем, что в главных осях тензор имеет диагональный вид:
. Действуя так же, как в задаче 29, найдем, что в главных осях тензор имеет диагональный вид:
 , (245)
, (245)
причем матрица преобразования имеет вид:
 (246)
(246)
Ясно, что в системе главных осей тензор  должен быть равен:
должен быть равен:
 (247)
(247)
Правильность этого определения подтверждается тем, что, если возвести (247) в квадрат, воспользовавшись формулой (185), то получим (245). Чтобы найти тензор  в первоначальной системе координат, воспользуемся законом преобразования компонент тензора второго ранга:
в первоначальной системе координат, воспользуемся законом преобразования компонент тензора второго ранга:  . Эту формулу удобнее записать в матричном виде, если под
. Эту формулу удобнее записать в матричном виде, если под  и
и  понимать матрицы второго порядка. Тогда, вспоминая из курса линейной алгебры операцию умножения матриц, можем записать:
понимать матрицы второго порядка. Тогда, вспоминая из курса линейной алгебры операцию умножения матриц, можем записать:
 ,
,
или  (248)
(248)
Входящие в правую часть матрицы определены формулами (246), (247), поэтому:

 (249)
(249)
Задача 35. В §27 было доказано, что диагональные компоненты тензора являются его нормальными составляющими в направлениях координатных осей. Доказательство было проведено для компоненты  . Доказать это утверждение для двух других диагональных компонент.
. Доказать это утверждение для двух других диагональных компонент.
Решение: Пусть единичный вектор  совпадает с ортом координатной оси
совпадает с ортом координатной оси  , т.е. с базисным вектором
, т.е. с базисным вектором  . Компоненты вектора
. Компоненты вектора  при этом равны:
при этом равны:  ,
,  . Подставляя их в формулу (227) и выполняя суммирование, получим:
. Подставляя их в формулу (227) и выполняя суммирование, получим:  . Аналогично, если вектор
. Аналогично, если вектор 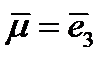 , то
, то  ,
,  и
и  .
.
Задача 36. Доказать формулы (226)-(228).
Решение: Тангенциальная составляющая  симметричного тензора 2-го ранга в направлениях
симметричного тензора 2-го ранга в направлениях 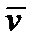 и
и  , т.е. в плоскости, определяемой этими векторами, была определена формулой (225). Если все главные значения тензора различны, то в системе главных осей он имеет вид (177). Подставляя в (225) и выполнив предусмотренное там суммирование, как раз и получим (226). Если два главных значения тензора совпадают, то он имеет вид (177), и тогда из (225) получим:
, т.е. в плоскости, определяемой этими векторами, была определена формулой (225). Если все главные значения тензора различны, то в системе главных осей он имеет вид (177). Подставляя в (225) и выполнив предусмотренное там суммирование, как раз и получим (226). Если два главных значения тензора совпадают, то он имеет вид (177), и тогда из (225) получим:  (250)
(250)
Единичные векторы 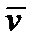 и
и  по определению ортогональны, т.е. их скалярное произведение
по определению ортогональны, т.е. их скалярное произведение  . Отсюда
. Отсюда  и подставив в (250), получим (227). Если же все три главных значения тензора одинаковы, то для
и подставив в (250), получим (227). Если же все три главных значения тензора одинаковы, то для  получим выражение (228). В силу ортогональности направлений
получим выражение (228). В силу ортогональности направлений 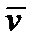 и
и 
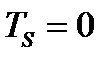 , т.е. все тангенциальные составляющие шарового тензора равны нулю.
, т.е. все тангенциальные составляющие шарового тензора равны нулю.
Задача 37. Решить систему (233).
Решение. Первые два уравнения системы будут удовлетворены, если  . Третья компонента
. Третья компонента  не может быть равна нулю, т.к. это противоречит последнему уравнению. Вместо этого из уравнения (233г) получаем, что
не может быть равна нулю, т.к. это противоречит последнему уравнению. Вместо этого из уравнения (233г) получаем, что 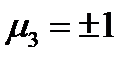 . Таким образом, первое решение будет такое:
. Таким образом, первое решение будет такое:  .
.  Аналогично получим еще два решения:
Аналогично получим еще два решения:  и
и  .
.
Пусть теперь только одна из компонент вектора 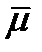 равна нулю, а две другие нет. Например,
равна нулю, а две другие нет. Например, 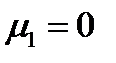 . Уравнения (233б, в) могут быть удовлетворены тогда только за счет обращения в нуль выражений в квадратных скобках. Получим:
. Уравнения (233б, в) могут быть удовлетворены тогда только за счет обращения в нуль выражений в квадратных скобках. Получим:  .
.
Приравняем левые части первых двух уравнений: 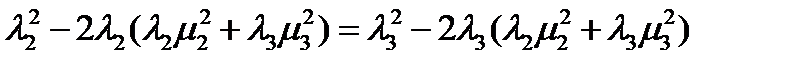 . Подставив сюда из третьего уравнения
. Подставив сюда из третьего уравнения  , после преобразований получим:
, после преобразований получим:  . Отсюда:
. Отсюда:  и
и  . Тогда
. Тогда  и решение будет такое:
и решение будет такое:  . Если
. Если  , то аналогично получаем
, то аналогично получаем  . Если же
. Если же  , то
, то 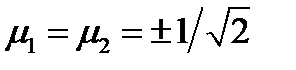 . Таким образом, еще два решения будут такими:
. Таким образом, еще два решения будут такими:  и
и  .
.
Осталось выяснить, имеет ли система (233) решения, когда все три компоненты  ,
,  ,
,  отличны от нуля. В этом случае система
отличны от нуля. В этом случае система
принимает вид:  .
.
Эту систему можно рассматривать как линейную относительно  ,
,
 ,
,  и
и  :
:  .
.
Определитель этой системы равен нулю:  . В силу этого система не совместна. Таким образом, других решений, кроме тех, что уже были найдены, система (233) не имеет.
. В силу этого система не совместна. Таким образом, других решений, кроме тех, что уже были найдены, система (233) не имеет.
Задача 38. Сколько действительных главных значений имеет антисимметричный тензор 2-го ранга?
Решение. У антисимметричного тензора 2-го ранга диагональные компоненты равны нулю, а недиагональные отличаются знаком. Поэтому характеристическое уравнение антисимметричного тензора имеет вид:
 , (251)
, (251)
или в развернутом виде:
 (252)
(252)
Отсюда видно, что одно главное значение равно нулю, а два других будут комплексными (точнее чисто мнимыми). Вследствие этого и соответствующие им главные векторы тоже будут комплексными. Таким образом, антисимметричный тензор имеет только одно действительное главное значение, равное нулю, и одно действительное главное направление.
Задача 39. Разложить тензор:  на шаровую часть и девиатор, и показать, что первый инвариант девиатора равен нулю.
на шаровую часть и девиатор, и показать, что первый инвариант девиатора равен нулю.
Решение: Разложение тензора на шаровую часть и девиатор определяется формулой (205) из §26. Имеем:
 . Тогда девиатор будет равен:
. Тогда девиатор будет равен:  . Разложение тензора
. Разложение тензора  будет теперь выглядеть так:
будет теперь выглядеть так:
 . Первый инвариант девиатора – это его след:
. Первый инвариант девиатора – это его след:  , ч.т.д.
, ч.т.д.
Задача 40. Определить главные значения девиатора для тензора 
Решение: Девиатор этого тензора находится так же, как в предыдущей задаче, и имеет вид: 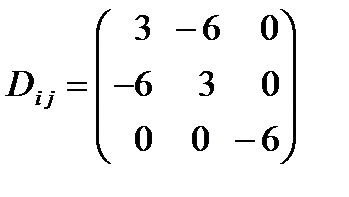 . Его главные значения можно найти, приравняв к нулю определитель:
. Его главные значения можно найти, приравняв к нулю определитель:  . Таким образом,
. Таким образом,  ,
,  ,
,  . Тот же результат получится, если сначала вычислить главные значения исходного тензора
. Тот же результат получится, если сначала вычислить главные значения исходного тензора  , а затем воспользоваться формулой (210). Для тензора
, а затем воспользоваться формулой (210). Для тензора  , как может убедиться читатель, главные значения равны
, как может убедиться читатель, главные значения равны  ,
,  ,
,  , откуда
, откуда  ,
,  ,
, 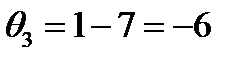 .
.
§29. Бескоординатная запись тензоров.
Для тензоров 1-го и 2-го рангов и операций с ними часто применяется бескоординатная запись. С такой формой записи по отношению к векторам (тензорам 1-го ранга) читатель знаком из курса векторной алгебры. Рассмотрим, как это переносится на тензоры 2-го ранга.
В типографски изданных книгах векторы обозначаются малыми латинскими или греческими буквами и жирным шрифтом. Тензоры 2-го ранга принято обозначать заглавными буквами и полужирным шрифтом. В рукописях и, в частности, в данном пособии, вектор обозначается чертой над буквой, тензор 2-го ранга – двумя чертами, тензор 3-го ранга – тремя чертами и т.д. (что, впрочем, применяется редко). Чаще для тензоров ранга выше 2-го используется все-таки запись в компонентах. Таким образом, для вектора, компонентами которого являются  , применяется символ
, применяется символ 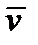 :
:  , для тензора 2-го ранга:
, для тензора 2-го ранга:  .
.
Произведение двух тензоров рангов  и
и  называется иначе внешним или упорядоченным произведением и дает тензор ранга
называется иначе внешним или упорядоченным произведением и дает тензор ранга  , например:
, например:  ,
,  ,
,
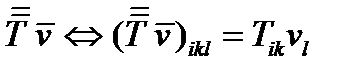 (253)
(253)
Внешнее произведение двух векторов  , как уже говорилось ранее, называется диадой.
, как уже говорилось ранее, называется диадой.
Внутреннее или скалярное произведение двух тензоров получается из внешнего произведения, если в нем произвести свертку по двум соседним инде
Популярное:

