Двойственный вектор и двойственный тензор.

⇐ ПредыдущаяСтр 7 из 11Следующая ⇒

Обобщением изложенного в предыдущем параграфе являются понятия двойственного вектора и двойственного тензора. Для всякого тензора 2-го ранга можно определить вектор посредством соотношения: 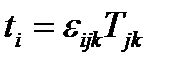, (145)

который называется вектором, двойственным тензору . Расписывая равенство подробно, получим:

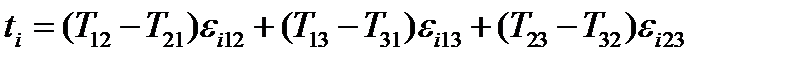Следовательно, компоненты двойственного вектора равны:

, , (146)

Если тензор антисимметричен, то , , . Если же тензор симметричен, то, как видно из (146), двойственный вектор равен нулевому вектору. Верно и обратное: равенство нулю двойственного вектора указывает на симметрию тензора. Для произвольного тензора 2-ого ранга двойственный вектор, как показывает формула (146), определяется только антисимметричной частью тензора. Двойственный вектор является аксиальным вектором (т.е. псевдовектором) в силу того, что - тензор – это псевдотензор. Формулу (145) можно обратить. Для этого умножим обе ее части на и воспользуемся последней формулой (119):

или 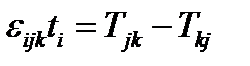(147)

Если тензор антисимметричен, то получаем:

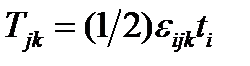(148)

Это соотношение можно рассматривать как определение антисимметричного тензора, двойственного данному вектору.

Иллюстрацией понятия двойственного вектора является векторное произведение. В параграфе 18 мы записали векторное произведение и в виде (125). Сравнив с формулой (145), видим, что векторное произведение и – это не что иное, как двойственный вектор по отношению к диадному произведению тех же векторов, которое, как известно, является тензором 2-ого ранга.

Формула (148) является обобщением формулы (144) и свидетельствует, что всякому вектору соответствует антисимметричный тензор второго ранга (бивектор). Этот факт позволяет взглянуть на векторное произведение под новым ракурсом.

Векторное произведение как антисимметричный тензор.

Векторное произведение двух векторов впервые появилось при изучении векторной алгебры и определялось там, как вектор, поставленный в соответствие по определенному правилу перемножаемым векторам. Познакомившись с понятием тензора, мы увидели, что в действительности векторное произведение – псевдовектор (аксиальный вектор). В тензорном анализе векторное произведение векторов и часто определяют как величину:

(149)

Видим, что это удвоенная антисимметричная часть диады , взятая со знаком минус, и потому являющаяся антисимметричным тензором 2-го ранга (бивектором). Три существенные компоненты этого бивектора являются компонентами векторного произведения в смысле определения векторной алгебры. В самом деле, матрица бивектора (149) выглядит так:

(150)

В параграфе 19 формулой (142) мы обозначили существенные компоненты бивектора как 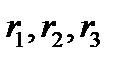. Сравнивая (150) и (142) видим, что: 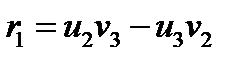; ; 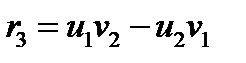(151)

А это и есть компоненты векторного произведения, как они были определены в векторной алгебре. Следовательно, векторное произведение двух векторов – это бивектор вида (149).

Задачи.

Задача 13 . Расшифровать следующие тензорные символы: , , , , .

Решение. а) представляет собой сумму: 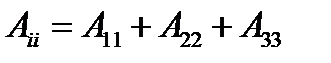и получается свёрткой тензора 2-ранга . Она называется следом тензора и обозначается или . След тензора 2-ого ранга равен сумме его диагональных компонент.

б) – это свертка тензора третьего ранга по двум последним индексам. Она равна . Результат этой свертки является тензором 1-ого ранга (вектором).

в) – это тензор 2-ого ранга. Он имеет девять компонент: , , , , , , , , .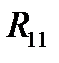

г) – получается в результате свертки произведения вектора и тензора 2-ого ранга 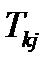( 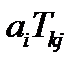). Это произведение является тензором 3-его ранга. В результате свертки по индексам и получается тензор, ранг которого меньше на два, т.е. тензор 1-ого ранга (вектор). В подробной записи это будет так: .

д) Рассмотрим произведение векторов , и тензора 2-ого ранга . Получим тензор 4-ого ранга 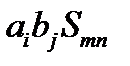. Произведем свертку по парам индексов и : . Суммируем по индексу : и далее по индексу . В результате получаем тензор нулевого ранга (скаляр):

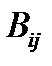Задача 14. Показать, что сумма является тензором 2-ого ранга, если известно, что и – тензоры 2-ого ранга.

Решение. При переходе к новой системе координат тензоры и преобразуются по закону, выраженному формулами (70), (72). Применяя формулу (72), получим: , . Отсюда: , а это значит, что указанная сумма преобразуется как тензор 2-ого ранга.

Задача 15. Показать, что .

Решение. В выражении все индексы являются немыми. Поскольку немые индексы можно обозначить любыми буквами, во втором слагаемом заменим индексы следующим образом: . Тогда второе слагаемое примет вид: . В третьем слагаемом немые индексы переобозначим так: . Тогда третье слагаемое будет иметь вид: . В результате получаем:

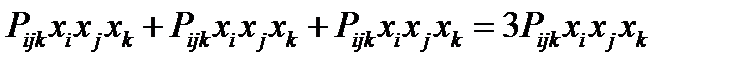Задача 16. – симметричный, – антисимметричный тензоры. Показать, что .

Решение. Так как и , то и . Поскольку все индексы являются немыми, то во втором слагаемом переобозначим индексы так: . Тогда 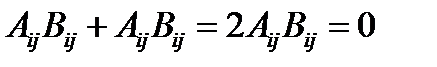. Отсюда .

Задача 17. Показать, что свернутое произведение произвольного тензора с симметричным тензором не зависит от антисимметричной части .

Решение. Разложим тензор на симметричную и антисимметричную части: .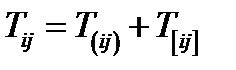

Тогда . В силу предыдущей задачи 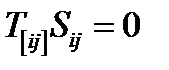, поэтому свертка содержит только симметричную часть тензора

Задача 18. Пусть физическая величина определена в прямоугольной системе координат двадцатью семью числами 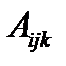. Пусть при переходе к другой системе координат величина преобразуется как вектор при любом выборе тензора . Доказать, что величины 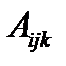представляют собой компоненты тензора 3-его ранга (один из вариантов теоремы деления тензоров).

Решение. Обозначим через вектор . В другой системе координат этот же вектор будет иметь компоненты , равные . Поскольку нам известно, что – это тензор 2-ого ранга, а – вектор, то ; . Тогда . Умножив обе части на , получим: . Отсюда . С другой стороны . Тогда и . Это равенство может выполняться для произвольного тензора только в том случае, если коэффициенты при компонентах равны нулю. Отсюда получаем: . Умножим обе части этого равенства на 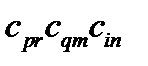: , или , т.е. .

Видим, что величины и преобразуются друг в друга как компоненты тензора 3-его ранга.

Задача 19. Доказать формулу (119) для - тензора.

Решение. а) . Здесь производится свертка по всем трем индексам. Распишем ее подробно, пользуясь определением символа Леви-Чивитты (117), (118).

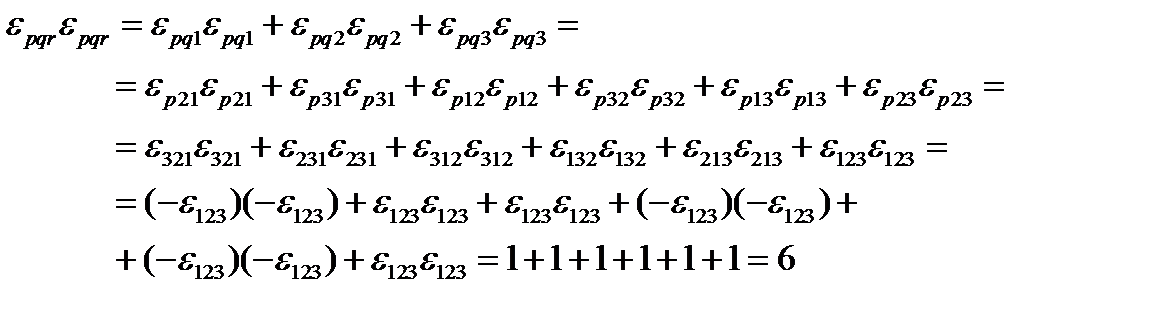
б) . Здесь производится свертка по двум парам индексов. В подробной записи:

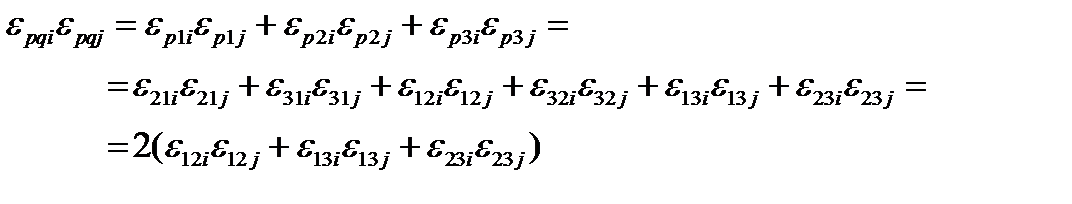
Каждое слагаемое по отдельности в скобках равно:

, ,

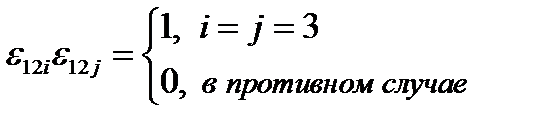Поэтому 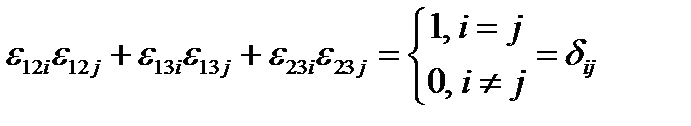. Отсюда .

Чтобы доказать третью формулу (119), вначале докажем вспомогательное тождество.

Задача 20. Доказать тождество:

(151)

Решение. Для доказательства рассмотрим определитель:

(152)

Известно, что перестановка строк и столбцов ведет к изменению знака определителя. Например,

Если менять местами строки произвольное число раз, то . А если менять местами столбцы, то .

Следовательно, для произвольной последовательности перестановок строк и столбцов получим:

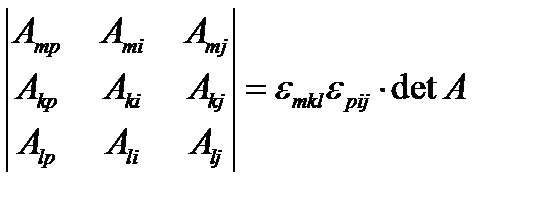(153)

Положим в определителе (152) :

. Определитель (153) при этом примет вид: , ч.т.д.

Задача 21. Используя тождество (151), доказать третью формулу (119), т.е. .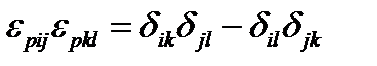

Решение. Разложим определитель в (151) по элементам первой строки:

Положим теперь :

ч.т.д.

Задача 22. Пользуясь свойствами и определением - тензора, доказать основные свойства векторного произведения.

Решение. В параграфе 18 показано, что векторное произведение векторов и может быть записано так: (154)

а) Покажем, что векторное произведение ортогонально к своим сомножителям. Умножим обе части (154), например, на :

Скалярное произведение равно нулю, а это и означает, что векторное произведение ортогонально вектору Аналогично доказываем, что векторное произведение ортогонально и второму сомножителю .

б) Докажем антикоммутативность векторного произведения. Векторное произведение на вектор определено формулой (154). Векторное произведение вектора на вектор будет равно: , ч.т.д.

в). Найдем модуль векторного произведения. Умножив обе части (154) на , получим квадрат модуля: .

В соответствии с формулой (121) в правой части стоит смешанное произведение векторов , , . Как известно, оно равно алгебраическому значению объема параллелепипеда, построенного на этих векторах. Поскольку в левой части стоит квадрат модуля, то правая часть положительна и векторы , , образуют правую тройку (если система координат правая). Кроме того, как было показано в п. а), ребро параллелепипеда ортогонально основанию, образованному векторами и . Поэтому объем параллелепипеда равен произведению длины ребра 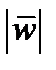на площадь основания. С другой стороны, этот же объем равен . Поэтому . Отсюда .

Задача 23 . Пользуясь определением и свойствами - тензора, доказать некоторые свойства смешанного произведения.

Решение. Смешанное произведение трех векторов , , с помощью - тензора записывается так:

(155)

а) Докажем, что если векторы , , компланарны, то их смешанное произведение равно нулю. Компланарные векторы лежат в одной плоскости. Но три вектора, лежащие в одной плоскости, обязательно будут линейно зависимыми. Это означает, что один из них представляет собой линейную комбинацию двух других. Например, или в координатах: . Смешанное произведение таких векторов будет равно:

Расписывая каждое слагаемое подробно, так же, как в задаче 22а, легко показать, что оба они равны нулю, т.е. равно нулю само смешанное произведение.

б) Докажем, что если переставить местами два сомножителя в смешанном произведении, то оно меняет знак: .

Поскольку здесь все индексы немые и их можно обозначить любыми буквами, то мы произвели замену индексов так: , .

в) Докажем, что при круговой перестановке сомножителей смешанное произведение не меняется:

Здесь мы произвели замену немых индексов так: , , .

Задача 24. Доказать, что двойное векторное произведение трех векторов можно представить в виде

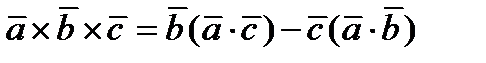(156).

Решение: Пользуясь - тензором, нетрудно получить, что:

Задача 25. Показать, что является бивектором и построить эквивалентный ему аксиальный вектор.

Решение. Как было определено в параграфе 19, бивектором называется антисимметричный тензор 2-ого ранга. Докажем вначале, что величины образуют тензор 2-ого ранга. Ограничившись только правыми системами координат, получим, что при преобразовании координат:

т.е. величины действительно преобразуются как компоненты тензора 2-ого ранга. Докажем теперь антисимметричность тензора : .

Как было показано в параграфе 19 (формула (143)), вектор, эквивалентный бивектору, равен . В данном случае:

Мы воспользовались здесь второй формулой (119). Таким образом, вектор, эквивалентный бивектору, совпадает с вектором .

Задача 26. Показать, что вектор, двойственный произвольному тензору , зависит только от его антисимметричной части .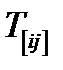

Решение. Вектор, двойственный произвольному тензору второго ранга 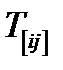, был определен в параграфе 20 формулой (145): .

Разложив тензор на симметричную и антисимметричную части, получим:

, (157)

где , .

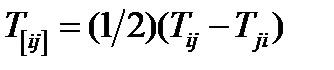Покажем, что первое слагаемое в (157), соответствующее симметричной части тензора , равно нулю: . Поскольку индексы – немые и их можно обозначить любыми буквами, то сделаем замену этих индексов: . Тогда: 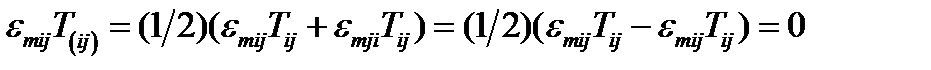, а это означает, что двойственный вектор от симметричной части тензора не зависит.

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒