
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Валишин А.А., Ожерелкова Л. М.Стр 1 из 11Следующая ⇒
Валишин А.А., Ожерелкова Л. М.
«Ортогональные тензоры.
Учебно-методическое пособие
Москва УДК 51 ББК 22.1
Рецензент: Д.ф.-м.н, профессор Ломовской В.А. (МИТХТ, каф. прикладной механики и основ конструирования).
Валишин А.А., Ожерелкова Л. М. «Ортогональные тензоры. Теория и примеры». Учебно-методическое пособие. М.: ИПЦ МИТХТ, 100 с.
Утверждено Библиотечно-издательской комиссией МИТХТ им. М. В. Ломоносова в качестве учебно-методического пособия. Поз. 64 /2014.
В пособии излагаются основы теории ортогональных тензоров, т.е. тензорная алгебра и элементы тензорного анализа в прямоугольных системах координат. Именно теория ортогональных тензоров чаще всего используется в приложениях, в первую очередь, в механике сполошных сред и кристаллофизике. Изложение материала сопровождается многочисленными примерами и задачами с решениями. Пособие предназначено для студентов, обучающихся по направлению «Прикладная математика». Пособие может быть так же полезно студентам других специальностей, а также молодым преподавателям, аспирантам и научным сотрудникам.
© МИТХТ им. М.В. Ломоносова, 2014 Оглавление. §1 Скаляры и векторы……………………………………………………. 4 §2. Задачи, приводящие к понятию тензора…………………………… 4 §3. Преобразование систем координат…………………………………. 11 §4. Правило суммирования Эйнштейна……………………………….. 15 §5. Преобразование координат точки и вектора………………………. 16 §6. Символ Кронекера…………………………………………………… 17 §7. Новое определние вектора…………………………………………… 19 §8. Задачи…………………………………………………………….……. 21 §9. Тензор второго ранга………………………………………….……… 24 §10. Транспонированный тензор………………………………………… 28 §11. Единичный тензор…………………………………………………… 28 §12. Симметричные и антисимметричные тензоры……………………. 28 §13. Задачи ……………………………………………………..…………. 30 §14. Геометрическая интерпретация тензоров первого и второго рангов 34 §15. Тензоры высших порядков………………………………………...… 36 §16. Операции с тензорами……………………………………………….. 38 §17. Теорема деления тензоров (критерий тензорности)………………. 41 §18. §19. Бивектор………………………………………………………………. 46 §20. Двойственный вектор и двойственный тензор……………………. 49 §21. Векторное произведение как антисимметричный тензор………… 50 §22. Задачи ………………………………………………………………… 51 §23. Главные значения и главные направления симметричного тензора второго ранга………………..………………………………. 59 §24. Степени тензоров второго ранга. Уравнение Гамильтона-Кэли… 67 §25. Круги Мора…………………………………………………………… 68 §26. Шаровой тензор и девиатор………………………………………… 73 §27. Нормальные и тангенциальные составляющие тензора второго ранга……………………………………………………...…. 74 §28. Задачи ………………………………………………………………… 79 §29. Бескоординатная запись тензоров………………………………….. 92 §30. Тензорные поля. Дифференцирование и интегрирование тензоров 93 Список литературы……………………………………………….………… 99
Скаляры и векторы. Из векторной алгебры известны понятия скаляра и вектора. Скалярами являются такие физические величины, как плотность, масса, объем, температура тела. Скаляры не связаны с понятием направления. При определении плотности или температуры бессмысленно говорить об изменении этих величин в каком-либо направлении. Такие ненаправленные физические величины называются скалярами. Значение скаляра полностью определяется заданием одного числа. Скаляры называются также тензорами нулевого ранга. В отличие от скаляров, другой тип физических величин, называемых векторами, может быть определен только по отношению к направлению. Механическая сила, скорость, напряженность электрического или магнитного поля, плотность тока, температурный градиент и т.д. – хорошо известные примеры векторов. Чтобы полностью определить вектор, необходимо задать как его величину (модуль вектора), так и направление. Можно определить вектор и по-другому. Рассмотрим прямоугольную декартову систему координат и зададим компоненты вектора вдоль каждой из осей координат. Компонента (или координата) вектора – это проекция вектора на данную ось. Если вектор
Таким образом, когда оси координат выбраны, вектор полностью определяется заданием значений трех его компонент вдоль осей. Векторы называются также тензорами первого ранга. Символ Кронекера. Перепишем формулы (27) и (29):
и подставим вторую в первую:
Распишем это подробно. Здесь двойное суммирование: по индексу
Следовательно:
Первые три формулы можно сокращенно записать так:
Следующие три формулы перепишем:
Объединяя эти две группы формул, можно записать:
Введем так называемый символ Кронекера:
С его помощью формулу (33) запишем в виде:
Вернемся к формулам (30) и подставим теперь первую во вторую:
Если это выражение расписать подробно, как (32), то в итоге получим:
Формулы (35) и (36) есть не что иное, как выражение свойств б) и в) ортогональной матрицы преобразования системы координат, сформулированные в § 3. Переставим местами в формуле (35) индексы
или т.е. символ Кронекера симметричен. Символ Кронекера обладает замечательным, так называемым фильтрующимсвойством, на котором и основано широкое применение этого символа. Рассмотрим выражение:
Это соотношение означает, что из всех компонент вектора Новое определение вектора. Пусть имеется вектор
Проиллюстрируем применение символа Кронекера для обращения формулы (40). Умножим обе части (40) на
При выводе (41) мы использовали формулы (36) и (39). Формулы (40) и (41) положены в основу нового определения вектора. Определение. Вектор – это геометрический объект, который в любой прямоугольной системе координат определяется тремя числами – его компонентами, которые при преобразовании системы координат преобразуются по формулам (40) и (41). Вектор существует независимо от системы координат, он инвариантен, а вот его координаты меняются при преобразованиях системы координат. Новое определение вектора сохраняет все известные из курса линейной алгебры операции с векторами: 1) Сложение векторов:
2) Сложение ассоциативно, т.е.
3) Умножение вектора на скаляр:
4) Дистрибутивность умножения:
Если компоненты вектора Рассмотрим скалярное произведение двух векторов
Докажем, что скалярное произведение – скаляр и инвариантно относительно преобразования системы координат. В новой системе координат компоненты векторов обозначим
Модуль вектора, определяемый скалярным произведением вектора самого на себя, запишется так:
Записывать квадрат модуля в виде
Поскольку компонентами единичного вектора являются направляющие косинусы или короче то Формула (51) линейна и однородна относительно направляющих косинусов. Она означает, что для любого направления в пространстве Формула (51) будет играть в дальнейшем определяющую роль, поскольку она допускает далеко идущие обобщения. §8. Задачи. Задача 1. Старая система координат Решение. Имеем:
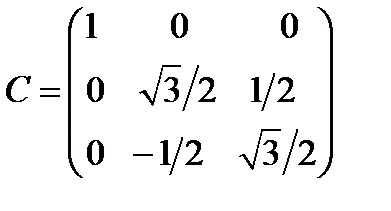 (52) (52)
Задача 2. Пусть новая система координат получена из старой в результате вращения вокруг оси Решение.
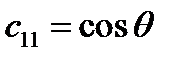 , , 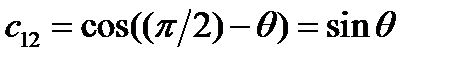 , ,
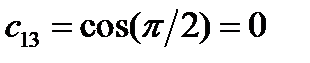 , ,
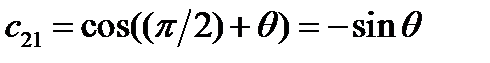 , , 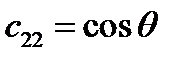 , ,

Тогда матрица преобразования имеет
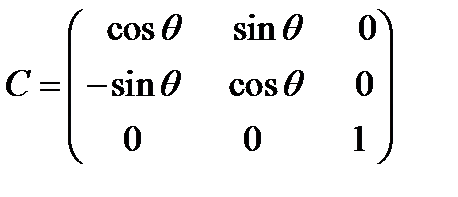 (53) (53)
Задача 3. Исследовать влияние преобразования координат
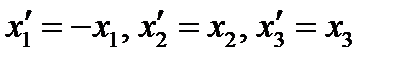 на компоненты вектора. на компоненты вектора.
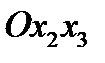 . Первоначальная правая система координат . Первоначальная правая система координат 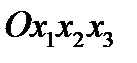 преобразуется в левую преобразуется в левую 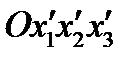 . Матрица преобразования имеет вид: . Матрица преобразования имеет вид: 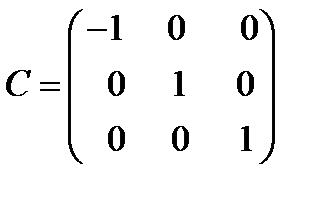 (54) (54)
Вектор преобразуется по формуле (40):
или
Таким образом, указанная инверсия изменяет только компоненту Задача 4. Найти преобразование компонент вектора при вращении, описанном в задаче 2. Решение. Используя матрицу преобразования (53) и формулу (55), получим:
Задача 5.. Доказать равенство Решение. Имеем:
Задача 6. Компоненты единичного вектора Решение. Необходимо доказать, что скалярное произведение
Задача 7. Доказать, что каждый элемент ортогональной матрицы преобразования Решение. Матрица перехода от старой системы координат к новой имеет вид (15). Ее определитель, как было показано в параграфе 3, равен
где Подчеркнем еще раз, что знак плюс берется тогда, когда обе системы координат, старая и новая, имеют одинаковую ориентацию и знак минус – в противном случае. Тензор второго ранга. Вспомним задачу, приведшую нас в параграфе 1 к понятию тензора напряжений, и формулу (12). Сравним ее с формулой (51). Формула (51) любому направлению в пространстве
Геометрический объект с таким свойством называется тензором второго ранга и обозначается Девять величин
которая называется матрицей тензора. Столбцы матрицы определяют три проекции тензора на координатные оси. В другой системе координат
Совместив
и наконец:
Стоящие в этих формулах косинусы – это элементы матрицы преобразования
Сокращенно это записывается так:
или еще короче: Видим, что закон преобразования проекций тензора такой же, как закон преобразования проекций вектора. Матрица тензора в новой системе координат состоит из компонент проекций тензора на эти новые оси. Первая проекция – вектор
называется матрицей тензора в новой системе координат. Таким образом, матрица тензора Установим связь между компонентами тензора в старой и новой системах координат. Обозначим компоненты векторов
Тогда первое равенство (64) в новых координатах запишется так:
Аналогично, две другие формулы (64) в новых координатах будут выглядеть так:
Или объединяя все три формулы:
По формуле (70) преобразуются компоненты тензора при переходе от старой системы координат к новой. Выведем обратную формулу. Умножим обе части (70) на
Умножим теперь обе части на или Формулы (70) и (72) определяют закон преобразования тензора второго ранга. Они положены в основу второго определения тензора. В любой прямоугольной системе координат тензор 2-го ранга определяется девятью компонентами, которые при преобразовании системы координат преобразуются по формулам (70) и (72).
Транспонированный тензор. Исследуем влияние перестановки индексов
То же самое сделаем в формуле (72), переставив индексы
Из (73) и (74) видно, что если Единичный тензор. Рассмотрим символ Кронекера
т.е. матрица
Задачи. Задача 8. Как преобразуются компоненты тензора 2-го ранга, если система координат подвергается преобразованию, описанному в задаче 1 параграфа 8? Решение. Исходим из формулы (70):
Матрица преобразования системы координат определена в (52). Имеем:
На этом примере, в частности, легко убедиться, что свойство симметричности и антисимметричности присуще самому тензору и не зависит от системы координат. Задача 9. Найти компоненты симметричного тензора в системе координат, получающейся с помощью преобразования, описанного в задаче 2 параграфа 8. Решение. По формуле (85), используя матрицу преобразования (53) и симметричного тензора, получаем:
В частности, если в старой системе координат матрица тензора была диагональной
то в новой системе:
Эти формулы обычно записывают в таком виде:
Матрица тензора в новой системе координат будет иметь вид:
Из (88)-(90) видно, что компонента тензора Задача 10. Необходимо повернуть тензор: Решение. Из (86) находим, что компонента 22 преобразуется по формуле: Решая его, получим:
Задача 11. Тензор электропроводности некоторого кристалла Популярное:
|
Последнее изменение этой страницы: 2016-04-10; Просмотров: 1255; Нарушение авторского права страницы