Нелинейные по параметрам парные уравнения регрессии.
1. Рассмотрим нелинейное уравнение регрессии 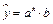 . Прологарифмируем обе части равенства
. Прологарифмируем обе части равенства 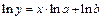 . Выполнив замену
. Выполнив замену 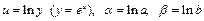 , получаем линейное уравнение регрессии
, получаем линейное уравнение регрессии 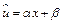 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
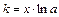 .
.
2. Прологарифмируем обе части уравнения регрессии 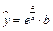
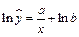 .
.
Сделаем замену 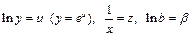 . В результате приходим к линейному уравнению регрессии
. В результате приходим к линейному уравнению регрессии 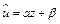 . Коэффициент эластичности вычисляется по формуле:
. Коэффициент эластичности вычисляется по формуле:
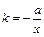 .
.
3. Аналогично приводится к линейному уравнению регрессии 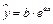 ,
, 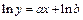 . Сделав замену
. Сделав замену 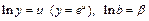 , получим
, получим 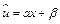 . Коэффициент эластичности находится по формуле
. Коэффициент эластичности находится по формуле
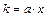 .
.
4. Рассмотрим уравнение 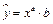 . После логарифмирования
. После логарифмирования 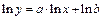 и замены
и замены 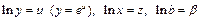 приходим к линейному уравнению регрессии
приходим к линейному уравнению регрессии 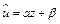 . Коэффициент эластичности
. Коэффициент эластичности
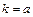 .
.
5. Рассмотрим показательно-степенную регрессию 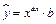 . После логарифмирования
. После логарифмирования 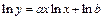 и замены
и замены 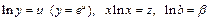 приходим к линейному уравнению регрессии
приходим к линейному уравнению регрессии 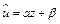 . Коэффициент эластичности находится по формуле
. Коэффициент эластичности находится по формуле
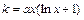 .
.
6. Рассмотрим нелинейную регрессию 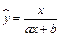 . Перепишем уравнение в виде
. Перепишем уравнение в виде 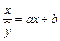 . После замены
. После замены 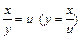 , приходим к линейному уравнению регрессии
, приходим к линейному уравнению регрессии 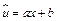 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
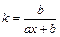 .
.
Во всех случаях, рассмотренных в п.1.1, 1.2 по крайней мере, в результате одной из замен 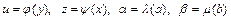 нелинейное уравнение регрессии сводится к линейному
нелинейное уравнение регрессии сводится к линейному 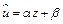 . В соответствии с (1.3), (1.5) формулы для оценки параметров принимают вид
. В соответствии с (1.3), (1.5) формулы для оценки параметров принимают вид
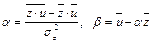 .
.
После этого из уравнений 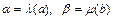 находим а и b и записываем уравнение регрессии в исходных переменных х и у.
находим а и b и записываем уравнение регрессии в исходных переменных х и у.
Для оценки адекватности нелинейной модели парной регрессии также используется критерий Фишера. Наблюдаемое значение критерия находится по формуле
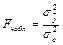 ,
,
где 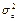 – дисперсия ошибок (ср. с SSE, MSE)
– дисперсия ошибок (ср. с SSE, MSE)
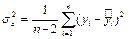 ,
,
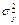 – сумма квадратов, которая объясняет регрессию (ср. с SSR, MSR)
– сумма квадратов, которая объясняет регрессию (ср. с SSR, MSR)
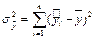 .
.
По заданному уровню значимости 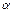 и числу степеней свободы
и числу степеней свободы 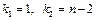 по таблице находится критическое значение
по таблице находится критическое значение 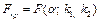 . Если
. Если 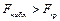 , то с надежностью
, то с надежностью 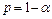 можно считать, что рассматриваемая математическая модель адекватна экспериментальным данным. В противном случае рассматриваемую парную регрессию нельзя считать адекватной.
можно считать, что рассматриваемая математическая модель адекватна экспериментальным данным. В противном случае рассматриваемую парную регрессию нельзя считать адекватной.
Коэффициент детерминации вычисляется по одной из формул
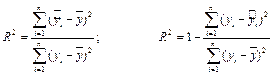 .
.
После этого можно вычислить индекс корреляции (корреляционное отношение).
Отметим, что наблюдаемое значение 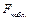 критерия Фишера можно выразить и через коэффициент детерминации по формуле
критерия Фишера можно выразить и через коэффициент детерминации по формуле
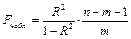 ,
,
где для парного уравнения регрессии 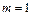 .
.
Доверительный интервал для промежуточных значений 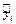 и прогноза
и прогноза 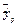 находится следующим образом:
находится следующим образом:
1) сначала находится доверительный интервал 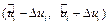 для промежуточных значений
для промежуточных значений 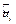 и доверительный интервал
и доверительный интервал 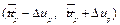 для прогноза
для прогноза 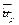 линейного уравнения регрессии
линейного уравнения регрессии 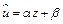 , где
, где
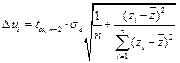
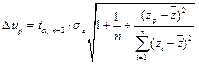
где 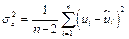 .
.
(ср. соответственно с формулами (1.25), (1.24));
2) затем по найденным значениям 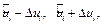
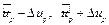 , используя связь между переменными и и y из уравнения
, используя связь между переменными и и y из уравнения 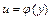 , находим соответствующие значения переменной y.
, находим соответствующие значения переменной y.
Пример решения задачи 1 контрольной работы.
На основе статистических данных показателя 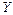 и фактора
и фактора 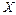 найти оценки параметров линии регрессии в предположении, что стохастическая зависимость между фактором
найти оценки параметров линии регрессии в предположении, что стохастическая зависимость между фактором 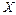 и показателем
и показателем 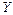 имеет вид
имеет вид 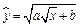 .
.
Используя критерий Фишера с надежностью 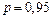 оценить адекватность принятой модели статистическим данным.
оценить адекватность принятой модели статистическим данным.
Найти:
- с надежностью 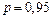 доверительную зону базисных данных;
доверительную зону базисных данных;
- точечную оценку прогноза;
- с надежностью 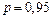 интервальную оценку прогноза;
интервальную оценку прогноза;
- оценки коэффициентов эластичности для базисных значений и прогноза.
Построить графики:
- фактических данных, линии регрессии и ее доверительной зоны – на одном графике;
- линии эластичности.
Исходные данные:
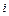
| 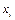
| 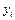
|
|
| 1, 7
| 2, 28
|
|
| 2, 9
| 2, 34
|
|
| 4, 4
| 2, 37
|
|
| 7, 8
| 2, 42
|
|
| 10, 9
| 2, 46
|
| прогноз
| 13, 0
| ?
|
Решение.
Преобразуем уравнение линии регрессии:
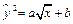 ,
,
и заменой переменных 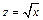 ,
, 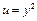 приведем уравнение регрессии к линейному:
приведем уравнение регрессии к линейному:
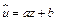 .
.
Исходные данные 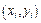 преобразуем с помощью формул
преобразуем с помощью формул
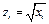 ,
, 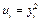 . (2.1)
. (2.1)
Оценки параметров 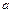 и
и 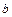 линейной модели найдем по формулам:
линейной модели найдем по формулам:
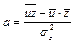 ; (2.2)
; (2.2)
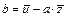 ; (2.3)
; (2.3)
где обозначено
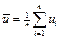 ;
; 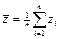 ;
;
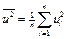 ;
; 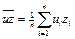 .
.
Для оценки параметров составим расчетную таблицу 2.1
На основе данных из таблицы для 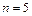 находим
находим
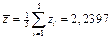 ;
;
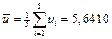 ;
;
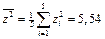 ;
;
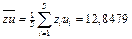 ;
;
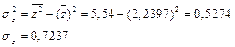 .
.
По формулам (2.2), (2.3) находим
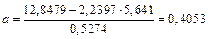 ;
;
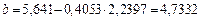 .
.
Получили уравнение стохастической зависимости (2.1) между 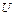 и
и 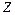 :
:
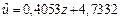 ,
,
которое соответствует зависимости между 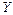 и
и 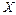 :
:
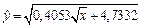 .
.
Для оценки адекватности полученной модели исходным данным найдем теоретические значения
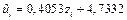 , а затем
, а затем 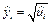 (см. табл. 2.1)
(см. табл. 2.1)
и величину 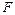 -критерия
-критерия
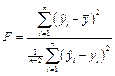 ,
,
Вычисление величин 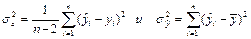 сведем в расчетную таблицу 2.1.
сведем в расчетную таблицу 2.1.
Находим
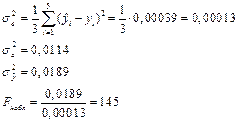
Вычислим коэффициент детерминации
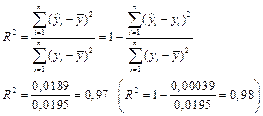
Результаты вычисления коэффициента детерминации по различным формулам практически совпадают, что свидетельствует о правильности вычислений.
Найдем индекс корреляции (корреляционное отношение) 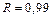 .
.
Для проверки вычислим наблюдаемое значение критерия Фишера по формуле 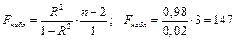
Значения 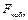 , найденные по различным формулам почти совпадают.
, найденные по различным формулам почти совпадают.
По таблице критических точек распределения 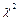 для
для 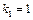 и
и 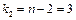 степеней свободы и
степеней свободы и 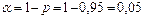 находим
находим 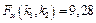 . Так как
. Так как 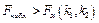 , то считаем, что построенная модель адекватна исходным данным.
, то считаем, что построенная модель адекватна исходным данным.
Для построения доверительной зоны исходных данных построим сначала доверительную зону для преобразованных данных 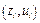 . Теоретические значения
. Теоретические значения 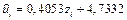 найдены выше (см. табл. 2.1). Найдем интервальные оценки для
найдены выше (см. табл. 2.1). Найдем интервальные оценки для 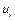 :
:
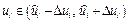 ,
,
где обозначено
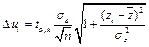 ,
,
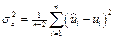 .
.
Величина 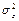 вычислена ранее:
вычислена ранее: 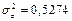 . Вычисление
. Вычисление 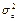 сведем в таблицу 2.1:
сведем в таблицу 2.1:
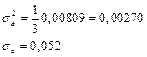
Величина 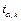 находится по таблице критических точек распределения Стьюдента для
находится по таблице критических точек распределения Стьюдента для 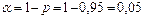 и
и 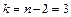 . Из таблицы находим
. Из таблицы находим 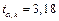 .
.
Находим 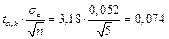 .
.
Формула для вычисления 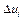 принимает вид
принимает вид
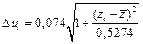 .
.
Значения 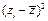 и
и 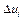 записываем в табл. 2.1. Далее находим
записываем в табл. 2.1. Далее находим 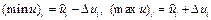 и границы доверительной зоны исходных данных
и границы доверительной зоны исходных данных
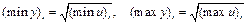
Результаты вычислений заносим в таблицу 2.1.
Точечную оценку прогноза найдем по формуле
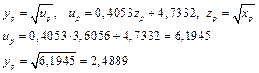
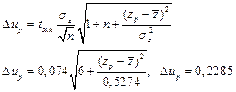
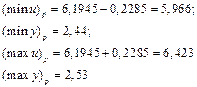
Таким образом, с вероятностью 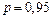 ,
, 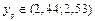 .
.
Найдем коэффициент эластичности заданной модели и его оценки при заданных 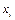 и
и 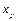 . По определению коэффициент эластичности равен
. По определению коэффициент эластичности равен
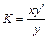 .
.
Для 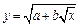 получаем
получаем
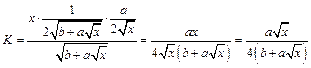
Оценки при заданных 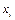 имеют вид
имеют вид
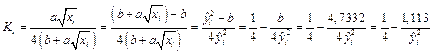
Аналогично,
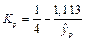
Значения 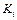 и
и 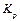 заносим в таблицу 2.1.
заносим в таблицу 2.1.
Строим графики фактических данных, линии регрессии и ее доверительной зоны:
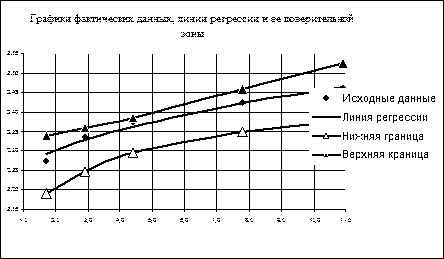
Строим график эластичности:
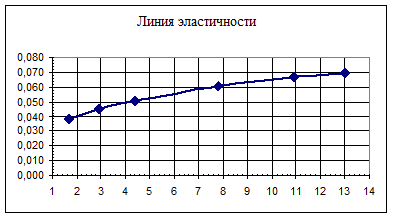
Выводы:
1. Уравнение регрессии имеет вид 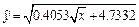 . Поскольку
. Поскольку 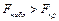 , то с вероятностью 0, 95 можно считать, что принятая математическая модель адекватна экспериментальным данным и на основе этой модели можно выполнять экономический анализ и находить значения прогноза.
, то с вероятностью 0, 95 можно считать, что принятая математическая модель адекватна экспериментальным данным и на основе этой модели можно выполнять экономический анализ и находить значения прогноза.
2. Для 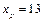 точечная оценка прогноза имеет значения
точечная оценка прогноза имеет значения 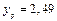 . С надежностью 0, 95 прогноз показателя будет иметь значения в интервале (2, 44; 2, 53).
. С надежностью 0, 95 прогноз показателя будет иметь значения в интервале (2, 44; 2, 53).
3. Для прогноза изменение фактора на 1% вызовет изменение показателя на 0, 07%.
Таблица 2.1
| 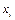
| 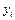
| 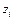
| 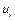
| 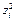
| 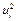
| 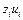
| 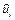
| 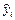
| 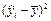
|
|
| 1, 7
| 2, 28
| 1, 3038
| 5, 1984
| 1, 70
| 27, 0234
| 6, 7777
| 5, 2616
| 2, 2938
| 0, 0064
|
|
| 2, 9
| 2, 34
| 1, 7029
| 5, 4756
| 2, 90
| 29, 9822
| 9, 3244
| 5, 4234
| 2, 3288
| 0, 0020
|
|
| 4, 4
| 2, 37
| 2, 0976
| 5, 6169
| 4, 40
| 31, 5496
| 11, 7820
| 5, 5834
| 2, 3629
| 0, 0001
|
|
| 7, 8
| 2, 42
| 2, 7928
| 5, 8564
| 7, 80
| 34, 2974
| 16, 3558
| 5, 8651
| 2, 4218
| 0, 0023
|
|
| 10, 9
| 2, 46
| 3, 3015
| 6, 0578
| 10, 90
| 36, 6969
| 19, 9998
| 6, 0713
| 2, 4640
| 0, 0081
|
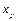
| 13, 0
|
| 3, 6056
|
|
|
|
| 6, 1945
| 2, 4889
|
|
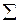
| 27, 7
| 11, 87
| 11, 1986
| 28, 2051
| 27, 70
| 159, 5495
| 64, 2397
|
|
| 0, 0189
|
| средние
| 5, 54
| 2, 374
| 2, 2397
| 5, 6410
| 5, 54
| 31, 9099
| 12, 8479
|
|
|
|
(продолжение таблицы 2.1.)
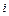
| 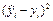
| 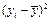
| 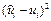
| 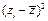
| 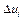
| 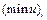
| 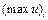
| 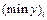
| 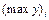
| 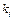
|
|
| 0, 00019
| 0, 0088
| 0, 00399
| 0, 8759
| 0, 1207
| 5, 1409
| 5, 3823
| 2, 27
| 2, 32
| 0, 038
|
|
| 0, 00013
| 0, 0012
| 0, 00272
| 0, 2882
| 0, 092
| 5, 3314
| 5, 5154
| 2, 31
| 2, 35
| 0, 045
|
|
| 0, 00005
| 0, 0000
| 0, 00112
| 0, 0202
| 0, 075
| 5, 5084
| 5, 6584
| 2, 35
| 2, 38
| 0, 051
|
|
| 0, 00000
| 0, 0021
| 0, 00008
| 0, 3059
| 0, 093
| 5, 7721
| 5, 9581
| 2, 40
| 2, 44
| 0, 060
|
|
| 0, 00002
| 0, 0074
| 0, 00018
| 1, 1274
| 0, 131
| 5, 9403
| 6, 2023
| 2, 43
| 2, 49
| 0, 067
|
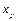
|
|
|
| 1, 8657
| 0, 2295
| 5, 9660
| 6, 4230
| 2, 44
| 2, 53
| 0, 069
|
| 0, 00039
| 0, 0195
| 0, 00809
|
|
|
|
|
|
|
|
| средние
|
|
|
|
|
|
|
|
|
|
|
Глава Ш.
Популярное:

