Контрольная работа по курсу «Эконометрия»
для студентов-заочников.
Задание 1
2) На основании статистических данных показателя 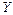 и фактора и фактора 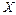 найти оценки параметров линии регрессии, если допустить, что стохастическая зависимость между фактором найти оценки параметров линии регрессии, если допустить, что стохастическая зависимость между фактором 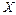 и показателем и показателем 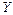 имеет вид: имеет вид: 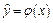 . (форма стохастической зависимости и статистические данные определяются из табл.3.9. Номер варианта совпадает с номером в студенческом журнале группы). . (форма стохастической зависимости и статистические данные определяются из табл.3.9. Номер варианта совпадает с номером в студенческом журнале группы).
3) Используя критерий Фишера с надежностью 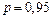 оценить адекватность принятой модели статистическим данным. оценить адекватность принятой модели статистическим данным.
4) Найти:
a) с надежностью 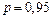 доверительную зону базисных данных: доверительную зону базисных данных:
b) точечную оценку прогноза;
c) с надежностью 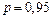 интервальную оценку прогноза; интервальную оценку прогноза;
d) оценки коэффициентов эластичности для базисных данных и прогноза;
e) оценку индекса корреляции.
5) Построить графики:
a) фактических данных;
b) линии регрессии и ее доверительную зону;
c) линию эластичности.
Таблица 3.9.
| № варианта
| Форма стохастической зависимости
| Исходные данные
| | 1.
| 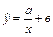
| Х 1, 01 1, 51 2, 02 2, 51 3, 01 3, 49
У 12, 03 8, 84 6, 99 6, 03 5, 55?
| | 2.
| 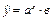
| Х 1, 02 1, 59 2, 12 2, 61 3, 05 3, 56
У 3, 02 2, 94 2, 71 3, 32 2, 69?
| | 3.
| 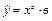
| Х 1, 1 1, 55 2, 09 2, 52 3, 07 3, 57
У 1, 84 2, 22 3, 54 3, 5 5, 3?
| | 4.
| 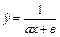 
| Х 1, 08 1, 53 2, 05 2, 58 3, 02 3, 58
У 4, 37 4, 01 3, 29 3, 1 3, 22?
| | 5.
| 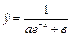
| Х 1, 1 1, 33 1, 58 1, 81 2, 09 2, 32
У 2, 72 2, 91 3, 18 3, 5 3, 71?
| | 6.
| 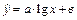
| Х 5, 12 10, 59 15, 07 21, 42 21, 73 32, 76
У 6, 5 7, 17 7, 39 7, 85 8, 01?
| | 7.
| 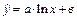
| Х 9, 35 15, 26 20, 67 26, 49 33, 14 39, 39
У 8, 68 9, 86 10, 65 11, 20 11, 87?
| | 8.
| 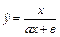
| Х 0, 21 0, 59 1, 03 1, 38 1, 71 2, 07
У 0, 19 0, 47 0, 67 0, 66 0, 92?
| | 9.
| 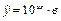
| Х 0, 32 0, 93 1, 59 2, 29 2, 92 3, 62
У 2, 44 3, 62 4, 98 5, 43 5, 59?
| | 10.
| 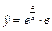
| Х 0, 32 0, 93 1, 59 2, 29 2, 92 3, 62
У 45, 71 5, 97 3, 82 3, 27 3, 06?
| | 11.
| 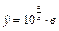
| Х 0, 38 0, 93 1, 61 2, 35 3, 02 3, 63
У 48, 33 7, 97 4, 60 4, 02 3, 75?
| | 12.
| 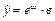
| Х 0, 11 0, 39 0, 66 0, 89 1, 15 1, 43
У 1, 78 2, 22 4, 30 5, 49 6, 57?
| | 13.
| 
| Х 1, 03 1, 63 2, 16 2, 61 3, 26 3, 77
У 1, 27 1, 42 1, 93 2, 35 2, 73?
| | 14.
| 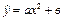
| Х 1, 15 1, 64 2, 28 2, 77 3, 42 3, 78
У 5, 44 7, 01 10, 62 13, 40 17, 42?
| | 15.
| 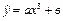
| Х 1, 01 1, 35 1, 71 2, 09 2, 49 2, 85
У 5, 02 5, 51 6, 52 7, 92 9, 64?
| | 16.
| 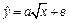
| Х 9, 33 15, 72 20, 87 26, 74 31, 95 37, 97
У 9, 67 11, 82 13, 76 13, 48 14, 99?
| | 17.
| 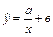
| Х 5, 97 6, 47 6, 98 7, 51 7, 99 8, 45
У 3, 70 3, 75 3, 72 3, 53 3, 25?
| | 18.
| 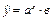
| Х 6, 04 6, 50 7, 01 7, 58 8, 04 8, 52
У 4, 49 4, 44 4, 83 4, 62 5, 01?
| | 19.
| 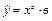
| Х 6, 06 6, 50 7, 00 7, 54 8, 00 8, 53
У 11, 30 12, 39 13, 16 14, 67 15, 50?
| | 20.
| 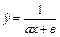
| Х 6, 06 6, 52 7, 02 7, 53 8, 05 8, 48
У 1, 89 2, 28 1, 46 1, 56 1, 73?
| | 21.
| 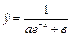
| Х 3, 69 3, 90 4, 20 4, 42 4, 72 4, 99
У 4, 55 4, 63 4, 61 4, 66 4, 66?
| | 22.
| 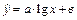
| Х 60, 23 67, 24 75, 37 82, 15 89, 20 94, 36
У 8, 65 8, 67 8, 84 8, 83 9, 01?
| | 23.
| 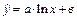
| Х 68, 79 74, 97 81, 39 87, 91 93, 94 100, 15
У 13, 71 13, 91 14, 11 14, 20 14, 38?
| | 24.
| 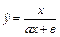
| Х 4, 23 4, 64 5, 00 5, 50 5, 98 6, 32
У 1, 85 1, 94 2, 11 2, 32 2, 45?
| | 25.
| 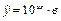
| Х 6, 90 7, 56 8, 21 8, 91 9, 57 10, 20
У 13, 99 17, 82 21, 32 25, 76 30, 26?
| | 26.
| 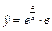
| Х 6, 90 7, 56 8, 21 8, 91 9, 57 10, 20
У 2, 41 2, 47 2, 41 2, 50 2, 45?
| | 27.
| 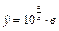
| Х 6, 99 7, 59 8, 30 9, 00 9, 64 10, 20
У 2, 55 2, 89 2, 44 2, 92 2, 89?
| | 28.
| 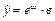
| Х 2, 72 2, 93 3, 13 3, 41 3, 63 3, 85
У 31, 95 41, 65 52, 00 73, 81 95, 47?
| | 29.
| 
| Х 6, 60 7, 20 7, 78 8, 35 8, 90 9, 42
У 17, 28 25, 25 36, 19 52, 81 76, 20?
| | 30.
| 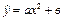
| Х 6, 79 7, 39 7, 84 8, 48 8, 57 9, 46
У 60, 03 68, 90 76, 80 89, 84 92, 49?
|
Задание 2.
1. Для заданных выборок значений величин 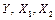 (варианты приведены в таблице 3.10, а данные – в таблице 3.11) найти выборочные средние (варианты приведены в таблице 3.10, а данные – в таблице 3.11) найти выборочные средние 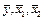 , выборочные дисперсии , выборочные дисперсии 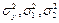 и выборочные средние квадратичные отклонения и выборочные средние квадратичные отклонения 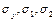 по формулам при по формулам при 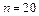 : :
2. Используя полученные данные, найти выборочные коэффициенты корреляции 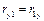 , , 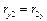 , , 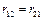 . Расчетные формулы: . Расчетные формулы:
где
Результаты записать в виде корреляционной матрицы:
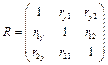
Используя критерий Стьюдента, проверить значимость коэффициентов 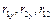 для чего вычислить для чего вычислить
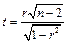
при 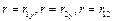 и сравнить с критическим значением и сравнить с критическим значением 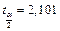 (для (для 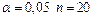 ). Коэффициент будет значимым, если ). Коэффициент будет значимым, если 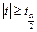 . .
3. Используя найденные коэффициенты корреляции, получить уравнения линейной регрессии 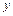 на на 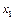 и и 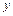 на на 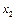 . Расчетные формулы: . Расчетные формулы:
Найти коэффициенты детерминации 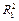 и и 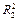 по формулам по формулам
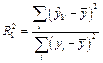 , ,  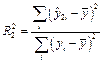
где
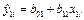 , , 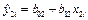 . .
4. Найти уравнение множественной регрессии 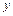 на на 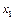 и и 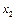 . Для этого сначала составить и решить систему уравнений . Для этого сначала составить и решить систему уравнений
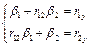 , ,
затем найти коэффициенты 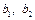 и и 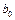 по формулам по формулам
и записать уравнение регрессии
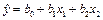 . .
5. Найти коэффициент множественной детерминации 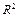
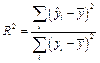 , ,
его скорректированное значение
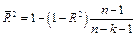 , ,
где 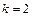 - число независимых переменных, проверить значимость - число независимых переменных, проверить значимость 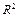 . Для этого вычислить наблюдаемое значение . Для этого вычислить наблюдаемое значение
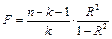
и сравнить его с критическим значением 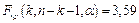 . Если . Если 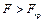 , гипотеза об одновременном равенстве нулю коэффициентов , гипотеза об одновременном равенстве нулю коэффициентов 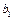 и и 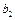 должна быть отвергнута. В этом случае хотя бы один из коэффициентов должна быть отвергнута. В этом случае хотя бы один из коэффициентов 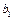 и и 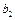 значимо отличается от нуля. значимо отличается от нуля.
6. Найти коэффициенты частной корреляции 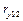 и и 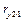 между между 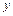 и одним из параметров при исключении влияния другого. Расчетные формулы: и одним из параметров при исключении влияния другого. Расчетные формулы:
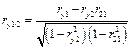 , ,
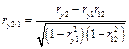 . .
Проверить значимость коэффициентов по критерию Стьюдента (см. пункт 2). Сделать выводы.
7. Используя критерий Дарбина-Уотсона, проверить данные на наличие автокорреляции. Для этого вычислить величины остатков 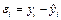 и величину и величину 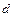 - статистики - статистики
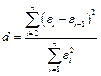 . .
Сравнить полученное значение со значениями 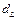 и и 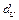 , найденными по таблице (для , найденными по таблице (для 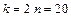 и и 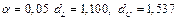 ). Если ). Если 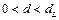 , имеется положительная автокорреляция, если , имеется положительная автокорреляция, если 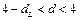 - отрицательная. При - отрицательная. При 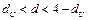 автокорреляция отсутствует. В остальных случаях нельзя сделать вывод ни о наличии автокорреляции, ни о ее отсутствии. автокорреляция отсутствует. В остальных случаях нельзя сделать вывод ни о наличии автокорреляции, ни о ее отсутствии.
Таблица 3.10. Варианты заданий.
Из таблицы 3.11 выбираются данные трех столбцов в соответствии с двумя последними цифрами номера зачетной книжки. Номера столбцов приведены ниже.
| №
| 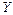
| 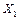
| 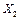
| №
| 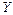
| 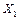
| 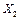
| |
|
| А1
| А2
| А3
|
|
| А2
| А3
| А8
| |
|
| А1
| А2
| А4
|
|
| А2
| А4
| А5
| |
|
| А1
| А2
| А5
|
|
| А2
| А4
| А6
| |
|
| А1
| А2
| А6
|
|
| А2
| А4
| А7
| |
|
| А1
| А2
| А7
|
|
| А2
| А4
| А8
| |
|
| А1
| А2
| А8
|
|
| А2
| А5
| А6
| |
|
| А1
| А3
| А4
|
|
| А2
| А5
| А7
| |
|
| А1
| А3
| А5
|
|
| А2
| А5
| А8
| |
|
| А1
| А3
| А6
|
|
| А2
| А6
| А7
| |
|
| А1
| А3
| А7
|
|
| А2
| А6
| А8
| |
|
| А1
| А3
| А8
|
|
| А2
| А7
| А8
| |
|
| А1
| А4
| А5
|
|
| А3
| А4
| А5
| |
|
| А1
| А4
| А6
|
|
| А3
| А4
| А6
| |
|
| А1
| А4
| А7
|
|
| А3
| А4
| А7
| |
|
| А1
| А4
| А8
|
|
| А3
| А4
| А8
| |
|
| А1
| А5
| А6
|
|
| А3
| А5
| А6
| |
|
| А1
| А5
| А7
|
|
| А3
| А5
| А7
| |
|
| А1
| А5
| А8
|
|
| А3
| А5
| А8
| |
|
| А1
| А6
| А7
|
|
| А3
| А6
| А7
| |
|
| А1
| А6
| А8
|
|
| А3
| А6
| А8
| |
|
| А1
| А7
| А8
|
|
| А3
| А7
| А8
| |
|
| А2
| А3
| А4
|
|
| А4
| А5
| А6
| |
|
| А2
| А3
| А5
|
|
| А4
| А5
| А7
| |
|
| А2
| А3
| А6
|
|
| А4
| А5
| А8
| |
|
| А2
| А3
| А7
|
|
| А4
| А6
| А7
|
Таблица 3.11. Данные для обработки.
| №
| А1
| А2
| А3
| А4
| А5
| А6
| А7
| А8
| |
| 3, 8
| 5, 2
| 3, 9
| 6, 8
| 2, 9
| 4, 1
| 4, 1
| 3, 8
| |
| 4, 7
| 3, 9
| 3, 7
| 4, 3
| 2, 1
| 4, 0
| 2, 2
| 4, 0
| |
| 4, 1
| 3, 9
| 3, 5
| 5, 4
| 2, 6
| 3, 8
| 2, 7
| 5, 5
| |
| 3, 9
| 5, 3
| 4, 3
| 7, 3
| 3, 5
| 4, 3
| 3, 6
| 6, 1
| |
| 5, 5
| 4, 8
| 3, 8
| 7, 3
| 4, 6
| 5, 8
| 3, 9
| 6, 9
| |
| 2, 9
| 1, 6
| 2, 8
| 3, 5
| 2, 0
| 3, 6
| 1, 6
| 3, 8
| |
| 4, 0
| 4, 1
| 2, 9
| 4, 8
| 3, 9
| 4, 7
| 2, 1
| 5, 5
| |
| 5, 0
| 6, 9
| 4, 6
| 7, 7
| 5, 0
| 5, 0
| 3, 5
| 6, 9
| |
| 5, 0
| 6, 6
| 3, 8
| 5, 0
| 4, 4
| 5, 1
| 4, 4
| 5, 5
| |
| 3, 9
| 4, 8
| 3, 2
| 5, 6
| 2, 9
| 4, 9
| 3, 8
| 5, 3
| |
| 4, 5
| 7, 0
| 4, 8
| 6, 9
| 3, 8
| 5, 2
| 3, 7
| 6, 4
| |
| 3, 4
| 5, 5
| 3, 6
| 5, 1
| 3, 0
| 5, 0
| 2, 9
| 4, 4
| |
| 4, 8
| 4, 4
| 3, 6
| 6, 7
| 3, 9
| 5, 1
| 3, 2
| 7, 1
| |
| 4, 1
| 5, 5
| 3, 4
| 5, 9
| 4, 2
| 3, 7
| 4, 2
| 5, 5
| |
| 3, 7
| 4, 4
| 3, 2
| 6, 1
| 3, 3
| 5, 3
| 2, 7
| 5, 7
| |
| 2, 3
| 4, 2
| 2, 8
| 5, 5
| 3, 4
| 3, 8
| 2, 6
| 4, 7
| |
| 3, 5
| 2, 9
| 1, 9
| 3, 7
| 2, 9
| 3, 3
| 1, 6
| 4, 3
| |
| 3, 3
| 4, 7
| 3, 7
| 6, 7
| 3, 3
| 4, 8
| 2, 3
| 5, 6
| |
| 4, 1
| 4, 3
| 3, 4
| 6, 6
| 4, 0
| 4, 6
| 3, 1
| 6, 3
| |
| 4, 9
| 6, 7
| 4, 7
| 6, 7
| 4, 1
| 6, 4
| 3, 7
| 7, 2
|
ЛИТЕРАТУРА
1. Лукьяненко И.Г., Красникова Л.И. Эконометрика. – К.: Знания, 1998.
2. Лукьяненко И.Г., Красникова Л.И. Эконометрика. Практикум с использованием компьютера. – К.: Знания, 1998.
3. Джонстон Дж. Эконометрические методы. – М.: Статистика, 1980.
4. Толбатов Ю.А. Эконометрика. – К.: Четверта хвиля, 1997.
5. Сударев В.П. Методические указания к семестровой работе по теме «Математическая обработка результатов наблюдений методами теории вероятностей, математической статистики и компьютерной графики». – Мариуполь, 1998, 2000.
6. В.П. Сударев. Расчетно-графическая работа по теме: Множественная корреляция». – Жданов, 1976.
СОДЕРЖАНИЕ
Популярное:
|

