Основные законы распределения одномерных случайных величин.
7.1 Биномиальное распределение  .
.
12.171 Дискретная случайная величина  имеет биномиальное распределение
имеет биномиальное распределение  , если:
, если:  ,
,  .
.
Доказать, что:  ,
, 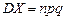 .
.
12.172 Найти математическое ожидание и дисперсию ДСВ  - числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна
- числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна  .
.
12.173 Найти дисперсию ДСВ  - числа появлений события
- числа появлений события  в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что
в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что 
12.174 Производятся независимые испытания с одинаковой вероятностью появления события  в каждом испытании. Найти вероятность появления события
в каждом испытании. Найти вероятность появления события  в одном испытании, если дисперсия числа появлений этого события в трёх независимых испытаниях равна
в одном испытании, если дисперсия числа появлений этого события в трёх независимых испытаниях равна  .
.
12.175 По одному из тиражей денежно-вещевой лотореи куплено 100 билетов. Среднее квадратичное отклонение числа выигравших билетов равно  . Найти вероятность выигрыша по одному билету лотореи.
. Найти вероятность выигрыша по одному билету лотореи.
12.176 Вероятность того, что при трёх выстрелах стрелок попадёт в цель, хотя бы один раз, равна  . Найти
. Найти  и
и 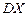 случайной величины
случайной величины  - числа попаданий при 20 выстрелах.
- числа попаданий при 20 выстрелах.
7.2 Распределение Пуассона  .
.
12.177 Дискретная случайная величина  имеет распределение Пуассона
имеет распределение Пуассона  если:
если: 
 ,
,  .
.
Доказать, что:  ,
,  .
.
12.178 В течение часа на станцию скорой помощи поступает случайное число вызовов  , распределённое по закону Пуассона с параметром
, распределённое по закону Пуассона с параметром  . Найти вероятности того, что в течение часа поступят: а) ровно два вызова; б) не более двух вызовов; в) не менее двух вызовов (Указание: принять
. Найти вероятности того, что в течение часа поступят: а) ровно два вызова; б) не более двух вызовов; в) не менее двух вызовов (Указание: принять  )
)
12.179 Число вызовов, поступающих на АТС (автоматическая телефонная станция) каждую минуту, распределено по закону Пуассона с параметром  . Найти вероятности того, что минуту на АТС поступят: а) ровно три вызова; б) хотя бы один вызов; в) менее пяти вызовов (Указание: принять
. Найти вероятности того, что минуту на АТС поступят: а) ровно три вызова; б) хотя бы один вызов; в) менее пяти вызовов (Указание: принять  ).
).
12.180 Вероятность, что в течение часа на станцию скорой помощи не поступит ни одного вызова, равна  . Считая, что число вызовов
. Считая, что число вызовов  , поступающих в течение часа на станцию, имеет распределение Пуассона, найти её математическое ожидание
, поступающих в течение часа на станцию, имеет распределение Пуассона, найти её математическое ожидание  и дисперсию
и дисперсию  .
.
7.3 Геометрическое распределение  .
.
12.181 Дискретная случайная величина  имеет геометрическое распределение
имеет геометрическое распределение  , если:
, если:  ,
,  .
.
Доказать, что:  ,
,  .
.
12.182 Производятся многократные испытания некоторого элемента на надёжность до тех пор, пока элемент не откажет. Вероятность отказа элемента в каждом испытании равна  . Составить закон распределения ДСВ
. Составить закон распределения ДСВ  - числа произведённых опытов и найти её математическое ожидание и дисперсию.
- числа произведённых опытов и найти её математическое ожидание и дисперсию.
12.183 Вероятность поражения цели равна 0.05. Производится стрельба по цели до первого попадания. Составить закон распределения ДСВ  - числа произведённых выстрелов и найти вероятность того, что для поражения цели потребуется сделать не менее пяти выстрелов.
- числа произведённых выстрелов и найти вероятность того, что для поражения цели потребуется сделать не менее пяти выстрелов.
12.184 В большой партии изделий вероятность брака равна  . Контроль качества проводится до первого появления бракованного изделия. В результате серии проверок обнаружено, что бракованное изделие впервые появлялось в среднем при десятом испытании. Найти вероятность брака
. Контроль качества проводится до первого появления бракованного изделия. В результате серии проверок обнаружено, что бракованное изделие впервые появлялось в среднем при десятом испытании. Найти вероятность брака  .
.
7.4 Равномерное распределение  .
.
12.185 Непрерывная случайная величина  имеет равномерное распределение
имеет равномерное распределение  , если:
, если: 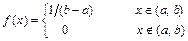 .
.
Доказать, что  ,
,  ,
,  .
.
12.186 Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 15мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус не более 5мин.
12.187 Цена деления шкалы измерительного прибора равна  . Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка: а) меньшая
. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка: а) меньшая  ; б) большая
; б) большая  .
.
12.188 Шкала рычажных весов, установленных в лаборатории, имеет цену деления 1г. При измерении массы химических компонентов смеси отсчёт делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность, что величина  - возможная ошибка определения массы по абсолютной величине не превысит величины среднего квадратичного отклонения возможных ошибок определения массы
- возможная ошибка определения массы по абсолютной величине не превысит величины среднего квадратичного отклонения возможных ошибок определения массы  .
.
12.189 Непрерывная случайная величина  имеет равномерное распределение на интервале
имеет равномерное распределение на интервале  , причём
, причём  ,
,  . Найти неизвестные постоянные
. Найти неизвестные постоянные  и
и  .
.
7.5 Показательное распределение 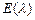 .
.
12.190 Непрерывная случайная величина  имеет показательное распределение
имеет показательное распределение 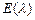 , если:
, если: 
 .
.
Доказать, что 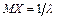 ,
,  ,
,  .
.
12.191 Непрерывная случайная величина  имеет показательное распределение:
имеет показательное распределение:  . Найти вероятность того, что
. Найти вероятность того, что  примет значение, меньшее математического ожидания
примет значение, меньшее математического ожидания  .
.
12.192 Длительность времени  безотказной работы элемента имеет показательное распределение
безотказной работы элемента имеет показательное распределение  . Вычислить вероятности того, что за время длительностью
. Вычислить вероятности того, что за время длительностью  элемент:
элемент:
а) выйдет из строя; б) будет работать.
12.193 Испытывают два независимо работающих элемента. Длительность времени безотказной работы первого элемента имеет показательное распределение  , второго -
, второго -  . Найти вероятность того, что за время длительностью
. Найти вероятность того, что за время длительностью  : а) оба элемента выйдут из строя; б) оба элемента будут работать; в) только один элемент выйдет из строя; г) хотя бы один элемент выйдет из строя.
: а) оба элемента выйдут из строя; б) оба элемента будут работать; в) только один элемент выйдет из строя; г) хотя бы один элемент выйдет из строя.
12.194 Время ожидания у бензоколонки АЗС является случайной величиной  , распределённой по показательному закону со средним временем ожидания, равным
, распределённой по показательному закону со средним временем ожидания, равным  . Найти вероятности следующих событий: а)
. Найти вероятности следующих событий: а)  ; б)
; б)  .
.
12.195 Дисперсия показательно распределённой случайной величины  равна
равна  . Найти вероятность
. Найти вероятность 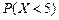 .
.
12.196 Время  (в годах) непрерывной работы электрической лампочки имеет показательное распределение.
(в годах) непрерывной работы электрической лампочки имеет показательное распределение.  -ным ресурсом элемента называется такое число
-ным ресурсом элемента называется такое число  , что за время
, что за время  элемент не выходит из строя с вероятностью
элемент не выходит из строя с вероятностью  . Найти вероятность того, что лампочка будет гореть в течение 2 лет, если её 90%-ный ресурс составляет 6 месяцев.
. Найти вероятность того, что лампочка будет гореть в течение 2 лет, если её 90%-ный ресурс составляет 6 месяцев.
7.6 Нормальное распределение  .
.
12.197 Непрерывная случайная величина имеет нормальное распределение  , если:
, если: 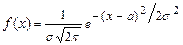 ,
,  .
.
Доказать, что  ,
,  .
.
Если  ~
~ 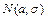 , то:
, то:
1) 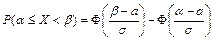 ; 2)
; 2)  , где
, где  -функция Лапласа, таблица значений которой приведена в приложении 6.2. При нахождении её значений для
-функция Лапласа, таблица значений которой приведена в приложении 6.2. При нахождении её значений для  следует учесть, что функция
следует учесть, что функция 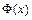 - нечётная, т.е.
- нечётная, т.е.  .
.
12.198 Математическое ожидание  и среднее квадратичное отклонение
и среднее квадратичное отклонение  нормально распределённой случайной величины
нормально распределённой случайной величины  соответственно равны 10 и 2. Найти вероятность того, что в результате испытания
соответственно равны 10 и 2. Найти вероятность того, что в результате испытания  примет значение, заключённое в интервале
примет значение, заключённое в интервале  .
.
12.199 Станок-автомат штампует детали. Контролируется длина детали  , которая распределена нормально с математическим ожиданием (проектная длина), равным 50мм. Фактическая длина изготовленных деталей не менее 32 и не более 68мм. Найти вероятность того, что длина наудачу взятой детали: а) больше
, которая распределена нормально с математическим ожиданием (проектная длина), равным 50мм. Фактическая длина изготовленных деталей не менее 32 и не более 68мм. Найти вероятность того, что длина наудачу взятой детали: а) больше  ; б) меньше
; б) меньше  (Указание: из равенства
(Указание: из равенства  предварительно найти
предварительно найти  ).
).
12.200 Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратичным отклонением  . Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине
. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине  .
.
12.201 Случайные ошибки измерения подчинены нормальному закону со средним квадратичным отклонением  и математическим ожиданием
и математическим ожиданием 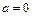 . Найти вероятность, что из 3 независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине
. Найти вероятность, что из 3 независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине 
12.202 Станок-автомат изготовляет валики, причём контролируется их диаметр  . Считая, что
. Считая, что  - нормально распределённая случайная величина с математическим ожиданием
- нормально распределённая случайная величина с математическим ожиданием  и средним квадратичным отклонением
и средним квадратичным отклонением  , найти интервал, симметричный относительно математического ожидания, в котором с вероятностью
, найти интервал, симметричный относительно математического ожидания, в котором с вероятностью  будут заключены диаметры изготовленных валиков.
будут заключены диаметры изготовленных валиков.
12.203 Рост мужчин определённой возрастной группы распределён по нормальному закону с математическим ожиданием 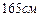 и средним квадратичным отклонением
и средним квадратичным отклонением 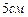 . Какую долю (в %) костюмов третьего роста следует предусмотреть в общем объёме производства для данной возрастной группы? (Указание: третий рост-
. Какую долю (в %) костюмов третьего роста следует предусмотреть в общем объёме производства для данной возрастной группы? (Указание: третий рост-  ).
).
12.204 Мастерская изготовляет стержни, длина которых представляет собой нормально распределённую случайную величину с математическим ожиданием  и средним квадратичным отклонением
и средним квадратичным отклонением  . Какую точность
. Какую точность  длины стержня мастерская может гарантировать в этом случае с вероятностью
длины стержня мастерская может гарантировать в этом случае с вероятностью  ?
?
12.205 Длина куска обоев в рулоне – случайная величина, распределённая по нормальному закону с математическим ожиданием 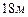 и средним квадратичным отклонением
и средним квадратичным отклонением  . Найти вероятность того, что длина куска в случайно выбранном рулоне будет не меньше
. Найти вероятность того, что длина куска в случайно выбранном рулоне будет не меньше  .
.
12.206 Коробки с конфетами упаковываются автоматически. Их средняя масса равна  . Известно, что
. Известно, что  коробок имеют массу, меньшую
коробок имеют массу, меньшую 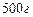 . Каков процент коробок, масса которых отличается от средней массы по абсолютной величине не более, чем на
. Каков процент коробок, масса которых отличается от средней массы по абсолютной величине не более, чем на  ?
?
12.207 Станок-автомат заполняет банки кофе. Масса кофе - случайная величина  ~
~ 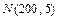 , а масса банки – случайная величина
, а масса банки – случайная величина  ~
~  . Найти вероятность того, что масса готовой к продаже банки с кофе будет не менее
. Найти вероятность того, что масса готовой к продаже банки с кофе будет не менее  . (Указание. Рассмотреть случайную величину
. (Указание. Рассмотреть случайную величину  - масса банки с кофе).
- масса банки с кофе).
12.208 Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределённая по нормальному закону с математическим ожиданием  и средним квадратичным отклонением
и средним квадратичным отклонением  . Локомотив может тянуть состав массой не более
. Локомотив может тянуть состав массой не более 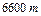 , в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется. (Указание. Рассмотреть случайную величину
, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется. (Указание. Рассмотреть случайную величину  , где
, где  - масса одного вагона).
- масса одного вагона).
12.209 Работа аппарата, расфасовывающего стиральный порошок в пакеты, подчиняется нормальному закону распределения со средним квадратичным отклонением  . Аппарат может быть настроен на любой средний вес упаковки с точностью до грамма. На какой средний вес должен быть настроен аппарат, если требуется, чтобы не более
. Аппарат может быть настроен на любой средний вес упаковки с точностью до грамма. На какой средний вес должен быть настроен аппарат, если требуется, чтобы не более 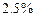 пакетов содержали меньше, чем
пакетов содержали меньше, чем  стирального порошка?
стирального порошка?
12.210 Средний срок безотказной работы телевизора определённой марки составляет  месяцев со средним квадратичным отклонением
месяцев со средним квадратичным отклонением  месяцев. Привлекая покупателей, производитель хочет дать гарантию на телевизор данной марки, обещая заменить его на новый в случае поломки до определённого срока. Предполагается, что срок службы подчиняется нормальному закону. Какой срок гарантии
месяцев. Привлекая покупателей, производитель хочет дать гарантию на телевизор данной марки, обещая заменить его на новый в случае поломки до определённого срока. Предполагается, что срок службы подчиняется нормальному закону. Какой срок гарантии  следует установить производителю, если он согласен заменять только
следует установить производителю, если он согласен заменять только  проданных телевизоров с наиболее коротким сроком работы?
проданных телевизоров с наиболее коротким сроком работы?
Популярное:

