Дискретные двумерные случайные величины.
Совокупность случайных величин  , заданных на одном и том же вероятностном пространстве
, заданных на одном и том же вероятностном пространстве 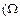 , A,
, A,  ), называют многомерной (
), называют многомерной ( 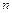 -мерной) случайной величиной (случайным вектором ). Ограничимся рассмотрением двумерных случайных величин
-мерной) случайной величиной (случайным вектором ). Ограничимся рассмотрением двумерных случайных величин 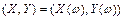 ,
,  .
.
Функцией распределения случайного вектора  называется функция
называется функция 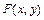 действительных переменных
действительных переменных  и
и 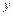 ,
,  , определяемая формулой
, определяемая формулой  .
.
Вероятность попадания случайной точки  в прямоугольник
в прямоугольник  ,
,  вычисляется по формуле:
вычисляется по формуле:
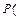
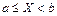 ,
, 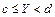 )
)  .
.
Зная функцию распределения (совместную) вектора  , можно найти функцию распределения (частную) каждой компоненты:
, можно найти функцию распределения (частную) каждой компоненты:
 ,
,  .
.
Случайные величины  и
и  называются независимыми, если для всех
называются независимыми, если для всех  :
: 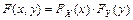 . В противном случае случайные величины называют зависимыми.
. В противном случае случайные величины называют зависимыми.
Случайный вектор  называется дискретным случайным вектором, если каждая из его компонент является дискретной случайной величиной. Ограничимся рассмотрением дискретных случайных величин
называется дискретным случайным вектором, если каждая из его компонент является дискретной случайной величиной. Ограничимся рассмотрением дискретных случайных величин  и
и  с конечным множеством возможных значений
с конечным множеством возможных значений  и
и  .
.
Функция распределения 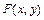 дискретного случайного вектора
дискретного случайного вектора  задаётся формулой
задаётся формулой 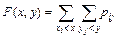 , где
, где  ,
, 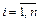 ,
,  и суммирование распространяется на все значения индексов
и суммирование распространяется на все значения индексов  и
и  для которых
для которых  и
и  .
.
Закон распределения дискретного случайного вектора  удобно задавать таблицей распределения (вероятностей), в которой перечислены все возможные пары значений
удобно задавать таблицей распределения (вероятностей), в которой перечислены все возможные пары значений  ),
), 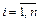 ,
,  компонент вектора и соответствующие им вероятности
компонент вектора и соответствующие им вероятности  , причём
, причём  .
.
Частные законы распределения  ,
, 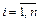 и
и  ,
,  компонент
компонент  и
и  , где
, где  ,
,  , можно найти, производя в таблице суммирования
, можно найти, производя в таблице суммирования  в каждой строке по столбцам и в каждом столбце по строкам.
в каждой строке по столбцам и в каждом столбце по строкам.
Дискретные случайные величины  и
и  независимы тогда и только тогда, когда
независимы тогда и только тогда, когда 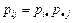 ,
, 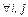 ,
,  ,
, 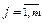 . В противном случае они зависимы.
. В противном случае они зависимы.
Ковариацией (корреляционным моментом) случайных величин  и
и  называют число
называют число  . Очевидно, что
. Очевидно, что  . Более удобной для вычисления
. Более удобной для вычисления  является формула
является формула  . Для независимых случайных величин
. Для независимых случайных величин  и
и  :
:  (необходимое условие независимости). Если
(необходимое условие независимости). Если  , то случайные величины
, то случайные величины  и
и  называют некоррелированными.
называют некоррелированными.
Коэффициентом корреляции случайных величин  и
и  называют число
называют число
 , где
, где  ,
,  .
.
Коэффициент корреляции обладает свойствами: 1)  ; 2)
; 2)  тогда и только тогда, когда
тогда и только тогда, когда  и
и  связаны линейной зависимостью
связаны линейной зависимостью  ,
,  ; 3) если
; 3) если  и
и  независимы, то
независимы, то 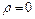 (необходимое условие независимости).
(необходимое условие независимости).
Условные законы распределения компоненты  при
при 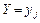 ,
, 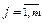 (индекс
(индекс  сохраняет одно и тоже значение при всех возможных значениях
сохраняет одно и тоже значение при всех возможных значениях  ) задают рядами распределения, указывая все возможные значения
) задают рядами распределения, указывая все возможные значения  и соответствующие им условные вероятности:
и соответствующие им условные вероятности:  ,
,  . Аналогично задают условные законы распределения компоненты
. Аналогично задают условные законы распределения компоненты  при
при 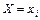 ,
,  :
:  ,
,  . Условные вероятности компонент
. Условные вероятности компонент  и
и  вычисляют соответственно по формулам:
вычисляют соответственно по формулам:
 ,
,  .
.
Числовые характеристики  ,
,  ,
,  ,
,  ,
,  , вычисляют по формулам:
, вычисляют по формулам:  ,
,  ,
,  ,
,
 ,
,  .
.
Условные математические ожидания дискретных случайных величин  и
и  при условиях
при условиях 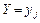 и
и 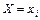 определяются соответственно формулами:
определяются соответственно формулами:
 ,
,  .
.
Вероятность события  , где
, где  - постоянная величина, вычисляется по формуле
- постоянная величина, вычисляется по формуле 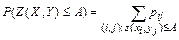 , где суммирование распространяется на все значения индексов
, где суммирование распространяется на все значения индексов  и
и  для которых
для которых 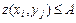 .
.
В задачах 12.211-12.214 закон распределения двумерной случайной величины  задан таблицей распределения вероятностей.
задан таблицей распределения вероятностей.
Требуется: а) найти законы распределения составляющих случайных величин  ,
,  и выяснить являются они зависимыми или нет;
и выяснить являются они зависимыми или нет;
б) вычислить 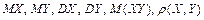 , а также вероятность
, а также вероятность  для указанных
для указанных  и
и  ;
;
в) найти условные законы распределения составляющих  и
и  при условии, что другая составляющая принимает указанные значения
при условии, что другая составляющая принимает указанные значения  и
и  , а также вычислить
, а также вычислить  ,
,  .
.
12.211  ,
,  ,
,  ,
, 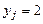 .
.
|
| Y
|
| X
|
|
|
|
|
| 0.05
| 0.1
| 0.25
|
|
| 0.15
| 0.2
| 0.25
|
12.212  ,
,  ,
,  ,
,  .
.
|
| Y
|
| X
|
|
|
|
|
| 0.12
| 0.18
| 0.3
|
|
| 0.08
| 0.12
| 0.2
|
12.213  ,
,  ,
, 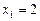 ,
,  .
.
|
| Y
|
| X
|
|
|
|
|
| 0.06
| 0.34
| 0.03
|
|
| 0.14
| 0.36
| 0.07
|
12.214 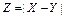 ,
,  ,
,  ,
,  .
.
|
| Y
|
| X
|
|
|
|
|
| 0.06
| 0.09
| 0.15
|
|
| 0.08
| 0.12
| 0.2
|
|
| 0.06
| 0.09
| 0.15
|
12.215 Бросается одна игральная кость. Требуется: а) составить закон распределения двумерной случайной величины  , где случайные величины
, где случайные величины  и
и  определяются следующим образом: если при подбрасывании игральной кости выпадает чётное число очков, то
определяются следующим образом: если при подбрасывании игральной кости выпадает чётное число очков, то  , в противном случае
, в противном случае  и
и  , когда число очков кратно трём, в противном случае
, когда число очков кратно трём, в противном случае  ; б) выяснить являются ли величины
; б) выяснить являются ли величины  ,
,  зависимыми и вычислить коэффициент корреляции
зависимыми и вычислить коэффициент корреляции  .
.
12.216 Бросаются две игральные кости. Требуется: а) составить закон распределения двумерной случайной величины  , где случайные величины
, где случайные величины  и
и  определяются следующим образом: если сумма очков на игральных костях чётная, то
определяются следующим образом: если сумма очков на игральных костях чётная, то  , в противном случае
, в противном случае  и
и  , если произведение очков на игральных костях – чётное число, в противном случае
, если произведение очков на игральных костях – чётное число, в противном случае  ; б) выяснить являются ли величины
; б) выяснить являются ли величины  ,
,  зависимыми и вычислить их ковариацию
зависимыми и вычислить их ковариацию  .
.
12.217 Число  выбирается случайным образом из множества целых чисел:
выбирается случайным образом из множества целых чисел:  . Затем из того же множества выбирается наудачу число
. Затем из того же множества выбирается наудачу число  , больше первого или равное ему. Составить закон распределения двумерной случайной величины
, больше первого или равное ему. Составить закон распределения двумерной случайной величины  и найти
и найти  .
.
12.218 Пусть  и
и  -произвольные случайные величины. Доказать, что:
-произвольные случайные величины. Доказать, что:
а) 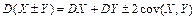 ,
,
б)  , где
, где  .
.
12.219 Случайные величины  и
и  имеют математические ожидания
имеют математические ожидания  ,
,  , дисперсии
, дисперсии  ,
,  и ковариацию
и ковариацию  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
.
12.220 Найти математические ожидания  ,
,  , дисперсии
, дисперсии  ,
,  и ковариацию
и ковариацию  случайных величин
случайных величин  и
и 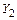 , если
, если 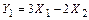 ,
, 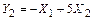 , а случайные величины
, а случайные величины  и
и  имеют следующие числовые характеристики:
имеют следующие числовые характеристики: 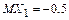 ,
,  ,
,  ,
,  ,
,  .
.
Популярное:

