Непрерывные двумерные случайные величины.
Случайный вектор  называется (абсолютно) непрерывным, если его функция распределения представляется в виде
называется (абсолютно) непрерывным, если его функция распределения представляется в виде 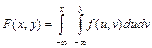 ,
,  ,
,  , где
, где 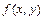 -неотрицательная и интегрируемая в бесконечных пределах функция, называемая функцией плотности вероятностей (совместной). Функция распределения
-неотрицательная и интегрируемая в бесконечных пределах функция, называемая функцией плотности вероятностей (совместной). Функция распределения 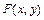 непрерывного случайного вектора
непрерывного случайного вектора  является непрерывной функцией на всей числовой плоскости.
является непрерывной функцией на всей числовой плоскости.
Функция 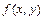 является плотностью вероятностей некоторого непрерывного случайного вектора
является плотностью вероятностей некоторого непрерывного случайного вектора  , тогда и только тогда, когда:
, тогда и только тогда, когда:
1)  ; 2)
; 2) 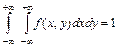 .
.
В точках непрерывности функции 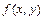 :
:  .
.
Для непрерывного случайного вектора  с плотностью вероятностей
с плотностью вероятностей 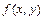 вероятность любого события вида
вероятность любого события вида  ,
,  вычисляется по формуле:
вычисляется по формуле:  .
.
Частные плотности вероятностей компонент находятся интегрированием совместной плотности:  ,
,  .
.
Непрерывные случайные величины  и
и  независимы тогда и только тогда, когда
независимы тогда и только тогда, когда  ,
,  . В противном случае они зависимы.
. В противном случае они зависимы.
Числовые характеристики  ,
,  вычисляют по формулам:
вычисляют по формулам: 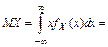
 ,
, 

Вероятность события  , где
, где  -постоянная величина, находится по формуле
-постоянная величина, находится по формуле  , где интегрирование распространяется на все значения переменных
, где интегрирование распространяется на все значения переменных  ,
,  для которых
для которых  .
.
В задачах 12.221-12.222 двумерная непрерывная случайная величина  задана совместной функцией распределения
задана совместной функцией распределения 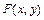 . Требуется: а) найти функции распределения составляющих случайных величин
. Требуется: а) найти функции распределения составляющих случайных величин  ,
,  и выяснить являются они зависимыми или нет; б) найти совместную функцию плотности вероятностей
и выяснить являются они зависимыми или нет; б) найти совместную функцию плотности вероятностей 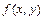 ; в) вычислить вероятность
; в) вычислить вероятность  для указанной области
для указанной области  .
.
12.221 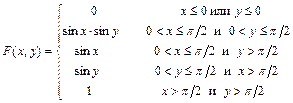
 - прямоугольник
- прямоугольник 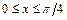 ,
,  .
.
12.222 
 - квадрат
- квадрат  ,
, 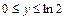 .
.
В задачах 12.223-12.224 двумерная случайная величина  задана совместной функцией плотности вероятностей
задана совместной функцией плотности вероятностей  .Требуется:
.Требуется:
а) найти неизвестную постоянную  ; б) найти функции плотности вероятностей составляющих случайных величин
; б) найти функции плотности вероятностей составляющих случайных величин  ,
,  и выяснить являются они зависимыми или нет; в) вычислить
и выяснить являются они зависимыми или нет; в) вычислить  ,
, 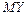 , а также вероятность
, а также вероятность  для указанного значения постоянной
для указанного значения постоянной  .
.
12.223 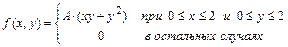
 .
.
12.224 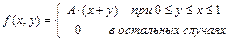
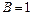 .
.
12.225 Двумерная случайная величина  равномерно распределена в указанной области
равномерно распределена в указанной области  . Найти: совместную функцию плотности вероятностей
. Найти: совместную функцию плотности вероятностей  ; функции плотности вероятностей составляющих случайных величин
; функции плотности вероятностей составляющих случайных величин  ,
,  и выяснить являются они зависимыми или нет; центр рассеивания
и выяснить являются они зависимыми или нет; центр рассеивания  , если: а)
, если: а)  ;
;
б)  ; в)
; в)  .
.
Функции случайных величин.
Пусть  - случайная величина, заданная на вероятностном пространстве
- случайная величина, заданная на вероятностном пространстве 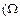 , A,
, A,  ) и
) и  - числовая функция, область определения которой включает в себя множество возможных значений
- числовая функция, область определения которой включает в себя множество возможных значений  . Случайную величину
. Случайную величину  , которая каждому
, которая каждому  ставит в соответствие число
ставит в соответствие число  называют функцией от скалярной случайной величины
называют функцией от скалярной случайной величины  и пишут
и пишут  .
.
Функция  от дискретной случайной величины
от дискретной случайной величины  также является дискретной. Если
также является дискретной. Если  задана рядом распределения
задана рядом распределения  ,
, 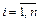 , то рядом распределения случайной величины
, то рядом распределения случайной величины  является ряд:
является ряд: 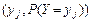 ,
,  ,
,  , где
, где  -различные числа среди чисел
-различные числа среди чисел  ,
,  ( суммирование распространяется на все значения индекса
( суммирование распространяется на все значения индекса  для которых
для которых  ).
).
Функция  от непрерывной случайной величины
от непрерывной случайной величины  может быть как непрерывной, так и дискретной случайной величиной.
может быть как непрерывной, так и дискретной случайной величиной.
Если  задана плотностью вероятностей
задана плотностью вероятностей  и
и  является монотонной (возрастающей или убывающей) дифференцируемой функцией, то плотность вероятностей случайной величины
является монотонной (возрастающей или убывающей) дифференцируемой функцией, то плотность вероятностей случайной величины  определяется формулой:
определяется формулой: 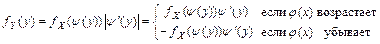 , где
, где  - функция, обратная к функции
- функция, обратная к функции  . Если
. Если  является дифференцируемой кусочно-монотонной (имеющей
является дифференцируемой кусочно-монотонной (имеющей  интервалов монотонности) функцией, то плотность вероятностей случайной величины
интервалов монотонности) функцией, то плотность вероятностей случайной величины  определяется формулой
определяется формулой  , где
, где  - функция, обратная к функции
- функция, обратная к функции  на
на  -ом интервале её монотонности (возрастания или убывания).
-ом интервале её монотонности (возрастания или убывания).
Для вычисления числовых характеристик неслучайной функции от случайной величины  можно не знать закон распределения зависящей от
можно не знать закон распределения зависящей от  случайной величины
случайной величины  , а достаточно знать закон распределения случайного аргумента
, а достаточно знать закон распределения случайного аргумента  . Математическое ожидание и дисперсия случайной величины
. Математическое ожидание и дисперсия случайной величины  , если они существуют, могут быть найдены по формулам:
, если они существуют, могут быть найдены по формулам:
1)  ,
,  , если дискретная случайная величина
, если дискретная случайная величина  задана рядом распределения
задана рядом распределения  ,
, 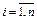 , где
, где 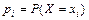 ; 2)
; 2)  ,
,  , если непрерывная случайная величина
, если непрерывная случайная величина  задана плотностью вероятностей
задана плотностью вероятностей  .
.
Пусть  - случайная вектор, заданный на вероятностном пространстве
- случайная вектор, заданный на вероятностном пространстве 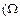 , A,
, A,  ) и
) и  - числовая функция, область определения которой включает в себя множество возможных значений
- числовая функция, область определения которой включает в себя множество возможных значений  . Случайную величину
. Случайную величину  , которая каждому
, которая каждому  ставит в соответствие число
ставит в соответствие число  называют функцией от случайного вектора
называют функцией от случайного вектора  и пишут
и пишут  .
.
Функция  от дискретного случайного вектора
от дискретного случайного вектора  также является дискретной. Если
также является дискретной. Если  задан таблицей распределения
задан таблицей распределения  ,
, 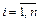 ,
,  , где
, где  , то рядом распределения случайной величины
, то рядом распределения случайной величины  является ряд:
является ряд: 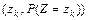 ,
,  , где
, где  - различные числа среди чисел
- различные числа среди чисел  ,
, 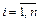 ,
,  ,
,  (суммирование распространяется на все значения индексов
(суммирование распространяется на все значения индексов  и
и  для которых
для которых  ).
).
Для вычисления числовых характеристик неслучайной функции от случайного вектора  достаточно знать закон распределения случайного аргумента
достаточно знать закон распределения случайного аргумента  . Математическое ожидание и дисперсия случайной величины
. Математическое ожидание и дисперсия случайной величины  , если они существуют, могут быть найдены по формулам:
, если они существуют, могут быть найдены по формулам:
1)  ,
,  , если дискретный случайный вектор
, если дискретный случайный вектор  задан таблицей распределения
задан таблицей распределения  ,
, 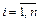 ,
,  , где
, где  ;
;
2)  ,
,  , если непрерывный случайный вектор
, если непрерывный случайный вектор  задан совместной плотностью вероятностей
задан совместной плотностью вероятностей 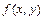 .
.
12.226 Дискретная случайная величина  задана рядом распределения
задана рядом распределения 
 . Найти распределение случайной величины
. Найти распределение случайной величины  и вычислить
и вычислить 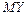 , если:
, если:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
12.227 Распределение двумерной дискретной случайной величины  задаётся таблицей распределения вероятностей:
задаётся таблицей распределения вероятностей:
|
| Y
|
| X
| 
|
|
|

| 0.07
| 0.1
| 0.13
|
|
| 0.2
| 0.23
| 0.27
|
Найти ряд распределения вероятностей случайной величины  и вычислить
и вычислить  , если:
, если:
а)  ; б)
; б)  .
.
12.228 Непрерывная случайная величина  , возможные значения которой заключены в интервале
, возможные значения которой заключены в интервале 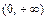 , задана функцией плотности вероятностей
, задана функцией плотности вероятностей  . Найти функцию плотности вероятностей
. Найти функцию плотности вероятностей  случайной величины
случайной величины  , если:
, если:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 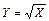 .
.
12.229 Непрерывная случайная величина  равномерно распределена в интервале
равномерно распределена в интервале  . Найти функцию плотности вероятностей
. Найти функцию плотности вероятностей  случайной величины
случайной величины  , если:
, если:
а)  ; б)
; б) 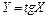 ; в)
; в) 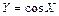 .
.
12.230 Непрерывная случайная величина  имеет нормальный закон распределения
имеет нормальный закон распределения  ~
~  . Доказать, что линейная функция
. Доказать, что линейная функция  также имеет нормальный закон распределения, причём
также имеет нормальный закон распределения, причём  ,
,  .
.
12.231 Случайная величина  задана функцией плотности вероятностей
задана функцией плотности вероятностей  . Найти математическое ожидание функции
. Найти математическое ожидание функции  , если:
, если:
а)  б)
б) 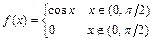 .
.
12.232 Рассматривая диаметр круга  как случайную величину, распределённую равномерно в интервале
как случайную величину, распределённую равномерно в интервале  , найти математическое ожидание площади круга
, найти математическое ожидание площади круга 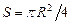 .
.
12.233 Рассматривая ребро куба как случайную величину  , распределённую равномерно в интервале
, распределённую равномерно в интервале  , найти математическое ожидание объёма куба
, найти математическое ожидание объёма куба  .
.
12.234 Непрерывная случайная величина  имеет показательное распределение с параметром
имеет показательное распределение с параметром  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
.
12.235 Случайные величины  и
и  независимы и распределены равномерно:
независимы и распределены равномерно:  - в интервале
- в интервале  ,
,  - в интервале
- в интервале  . Найти
. Найти  и
и 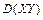 .
.
Популярное:

