Метод неопределенных коэффициентов
Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную, тригонометрическую функцию или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод применим лишь для ограниченного класса функций в правой части, таких как  или
или  . Кроме того, при решении этим методом справедлив п ринцип суперпозиции. Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида
. Кроме того, при решении этим методом справедлив п ринцип суперпозиции. Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида  и/или
и/или  , где Pn(x) и Qm(x) − многочлены степени n и m, соответственно, то частное решение дифференциального уравнения также будет являться суммой частных решений уравнений, построенных отдельно для каждого слагаемого в правой части.
, где Pn(x) и Qm(x) − многочлены степени n и m, соответственно, то частное решение дифференциального уравнения также будет являться суммой частных решений уравнений, построенных отдельно для каждого слагаемого в правой части.
Выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. Различные формы частного решения в зависимости от вида правой части и корней характеристического уравнения даны в таблице 2.
Таблица 2.
| №
| Вид правой части

| Корни характеристического уравнения
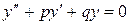
| Вид частного решения 
|
|
| а)
|
Pn(x)
| Число 0 не является корнем характеристического уравнения.
|

|
| б)
| Число 0 является корнем характеристического уравнения кратности s.
|
xs× 
|
|
| а)
|
Pn(x)× eax
| Число a не является корнем характеристического уравнения.
|
 × eax × eax
|
| б)
| Число a является корнем характеристического уравнения кратности s.
|
xs  × eax × eax
|
|
| а)
|
Pn(x)cosbx+  sinbx sinbx
| Числа ±bi не являются корнями характеристического уравнения.
|  cosbx+
+ cosbx+
+  sinbx
r = max(n, m). sinbx
r = max(n, m).
|
| б)
| Числа ±bi являются корнями характеристического уравнения.
| x×  cosbx +
+x× cosbx +
+x×  sinbx
r = max(n, m). sinbx
r = max(n, m).
|
|
| а)
|
Pn(x) × eax × cosbx +
+  × eax × sinbx × eax × sinbx
| Числа a ± bi не являются корнями характеристического уравнения.
|  eax× cosbx+
+ eax× cosbx+
+  × eax× sinbx
r = max(n, m). × eax× sinbx
r = max(n, m).
|
| б)
| Числа a ± bi являются корнями характеристического уравнения.
| x(  eaxcosbx+
+ eaxcosbx+
+  eax× sinbx)
r = max(n, m). eax× sinbx)
r = max(n, m).
|
Таблица 3
| n (степень многочлена Pn(x))
| 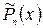
|
|
| 
|
|
| 
|
|
| 
|
|
| 
|
Задача 20. Найти общее решение уравнения  .
.
Решение. Находим общее решение  соответствующего однородного уравнения
соответствующего однородного уравнения  . Составляем характеристическое уравнение и решаем его:
. Составляем характеристическое уравнение и решаем его:  ,
,  ,
,  , следовательно, общее решение однородного уравнения будет иметь вид
, следовательно, общее решение однородного уравнения будет иметь вид  (таблица 1).
(таблица 1).
Правая часть  и число 0 не является корнем характеристического уравнения, имеем случай 1.а) таблицы 2. Частное решение ищем в виде:
и число 0 не является корнем характеристического уравнения, имеем случай 1.а) таблицы 2. Частное решение ищем в виде:  , (
, (  − многочлен 2-ой степени с неопределёнными коэффициентами (таблица 3)). Для определения коэффициентов
− многочлен 2-ой степени с неопределёнными коэффициентами (таблица 3)). Для определения коэффициентов  , найдём производные
, найдём производные  ,
,  и подставим их в исходное уравнение:
и подставим их в исходное уравнение:
 ,
, 
 ,
,
 .
.
Приравнивая коэффициенты при x с одинаковыми степенями в правой и левой частях равенства, получим:
при  :
: 
при 
при  ,
,
откуда  ,
, 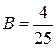 ,
,  .
.
Следовательно,  – частное решение.
– частное решение.
Общее решение исходного неоднородного уравнения в виде (29) запишется:
 .
.
Задача 21. Найти общее решение уравнения  .
.
Решение. Находим общее решение  соответствующего однородного уравнения
соответствующего однородного уравнения  . Характеристическое уравнение
. Характеристическое уравнение  или
или  имеет двукратный корень
имеет двукратный корень  . Следовательно, общее решение однородного уравнения:
. Следовательно, общее решение однородного уравнения:  (таблица 1).
(таблица 1).
Исследуем правую часть 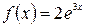 . Если представить её в виде
. Если представить её в виде  , то получим, что
, то получим, что  ,
,  т.е.
т.е.  ,
, 
 . Очевидно, что
. Очевидно, что  является двукратным корнем характеристического уравнения (
является двукратным корнем характеристического уравнения (  ). Имеем случай 2.б) таблицы 2. Поэтому частное решение
). Имеем случай 2.б) таблицы 2. Поэтому частное решение  будем искать в виде
будем искать в виде  , где
, где  – многочлен нулевой степени, т.е. число А (таблица 3).
– многочлен нулевой степени, т.е. число А (таблица 3).  .
.
Найдём производные  ,
,  и подставим их в исходное уравнение:
и подставим их в исходное уравнение:
 ,
,


Сократим обе части уравнения на  :
:
 , откуда 2А = 2, А = 1.
, откуда 2А = 2, А = 1.
Следовательно, частное решение исходного уравнения будет  , а его общее решение
, а его общее решение  или
или  .
.
Задача 22. Решить уравнение  .
.
Решение. Характеристическое уравнение  имеет два мнимых корня
имеет два мнимых корня  . Следовательно, общее решение однородного уравнения будет
. Следовательно, общее решение однородного уравнения будет  .
.
Правая часть уравнения имеет вид  .
.  (Таблица 2), где
(Таблица 2), где  ,
,  ,
,  ,
,  ,
, 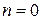 . Очевидно, что числа
. Очевидно, что числа  являются корнями характеристического уравнения. Имеем случай 3 б) таблицы 2. Поэтому частное решение
являются корнями характеристического уравнения. Имеем случай 3 б) таблицы 2. Поэтому частное решение  . Так как искомые многочлены
. Так как искомые многочлены  и
и  нулевой степени, т.е. числа A и B.
нулевой степени, т.е. числа A и B.
Найдём производные  ,
,  и подставим их в исходное уравнение:
и подставим их в исходное уравнение:


 ,
,
 .
.
Приравнивая коэффициенты при  и
и 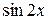 в левой и правой частях равенства, получим:
в левой и правой частях равенства, получим:
при  ;
;
при  , откуда
, откуда  ,
,  . Следовательно,
. Следовательно,  . Общее решение.
. Общее решение.  .
.
Задача 23. Найти общее решение уравнения  .
.
Решение. Характеристическое уравнение  имеет два корня
имеет два корня  . Следовательно, общее решение однородного уравнения будет
. Следовательно, общее решение однородного уравнения будет 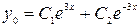 .
.
Исследуем правую часть  . Если представить её в виде
. Если представить её в виде  , то
, то  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Очевидно, что
. Очевидно, что  не являются корнями характеристического уравнения, Имеем случай 4 а) таблицы 2. Тогда частное решение
не являются корнями характеристического уравнения, Имеем случай 4 а) таблицы 2. Тогда частное решение  будем искать в виде
будем искать в виде  , где
, где  и
и  – многочлены нулевой степени, т.е. числа А и В. Следовательно,
– многочлены нулевой степени, т.е. числа А и В. Следовательно, 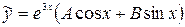 .
.
Найдём производные  ,
,  и подставим их в исходное уравнение:
и подставим их в исходное уравнение:
 ,
,
 ,
,

Сократим правую и левую части на  и приведём подобные:
и приведём подобные:
 .
.
Приравнивая коэффициенты при 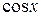 и при
и при  в левой и правой частях неравенства, получим:
в левой и правой частях неравенства, получим:
при  ;
;
при  , откуда
, откуда  ,
,  .
.
Следовательно,  .
.
Общим решением исходного уравнения будет функция
 .
.
Задача 24. Решить задачу Коши:  ,
,  ,
,  .
.
Решение. Характеристическое уравнение  имеет корни
имеет корни  ,
,  . Следовательно, общее решение однородного уравнения будет
. Следовательно, общее решение однородного уравнения будет  .
.
Правая часть уравнения  . Если представить её в виде
. Если представить её в виде  , то
, то  ,
,  ,
,  ,
, 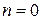 ,
,  . Очевидно, что
. Очевидно, что  не являются корнями характеристического уравнения, т.е. не совпадают с
не являются корнями характеристического уравнения, т.е. не совпадают с  . Имеем случай 3 а) таблицы 2. Степень искомых многочленов
. Имеем случай 3 а) таблицы 2. Степень искомых многочленов  , т.е.
, т.е.  =А и
=А и  =В. Таким образом,
=В. Таким образом,  .
.
Найдём производные  ,
,  и подставим их в исходное уравнение:
и подставим их в исходное уравнение:
 ,
,
 ,
,
 .
.
Приравнивая коэффициенты при 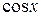 и
и  в левой и правой частях равенства, получим:
в левой и правой частях равенства, получим:
при  ;
;
при 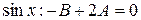 , откуда
, откуда  ,
, 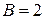 .
.
Следовательно,  . Общее решение запишем в виде:
. Общее решение запишем в виде:  .
.
В силу условия  получаем
получаем  . Далее найдём
. Далее найдём  . В силу условия
. В силу условия  , получим
, получим  . Для отыскания
. Для отыскания  и
и  необходимо решить систему
необходимо решить систему  , из которой
, из которой  ,
,  . Подставляя найденные значения произвольных постоянных в общее решение уравнения
. Подставляя найденные значения произвольных постоянных в общее решение уравнения  , найдём искомое частное решение, удовлетворяющее начальным условиям:
, найдём искомое частное решение, удовлетворяющее начальным условиям: 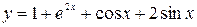 .
.
Задача 25. Решить уравнение  .
.
Решение. Общее решение соответствующего однородного уравнения

имеет вид (проверьте! )  . Данное дифференциальное уравнение представим в виде совокупности двух уравнений
. Данное дифференциальное уравнение представим в виде совокупности двух уравнений

Частное решение первого уравнения находим в виде:
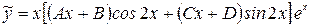 ,
,
так как  – корни характеристического уравнения
– корни характеристического уравнения
 ,
,  .
.
Соответствующие вычисления, которые предлагаем выполнить самостоятельно, дают
 .
.
Частное решение второго уравнения находим в виде  .
.
Определив значения коэффициентов, получим  .
.
Общее решение исходного уравнения имеет вид 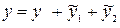 , т. е.
, т. е.
 .
.
Приведём примеры приложения теории дифференциальных уравнений второго порядка с постоянными коэффициентами к решению задач из курса теоретической механики.
Пример 3 . [5] Задание Д.2, стр. 130. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил.
Без учета сопротивления  дифференциальные уравнения движения имеют вид:
дифференциальные уравнения движения имеют вид:  .
.
Составляем характеристическое уравнение  , его решение
, его решение  . По таблице 1 общее решение уравнения
. По таблице 1 общее решение уравнения  имеет вид:
имеет вид:  Число 0 не является корнем характеристического уравнения, поэтому по таблице 2 вид 1а) частное решение уравнения
Число 0 не является корнем характеристического уравнения, поэтому по таблице 2 вид 1а) частное решение уравнения 
 .
.
Подставляем в  , получим
, получим  , отсюда
, отсюда  ,
,
тогда  .
.
Обратимся теперь к изучению движения точки с сопротивлением (стр.137)  . Дифференциальные уравнения примут вид
. Дифференциальные уравнения примут вид

Составляем характеристическое уравнение, решая его, получим
 (по условию n< l,
(по условию n< l,  рад/с.). Тогда по таблице 1 общее решение уравнения
рад/с.). Тогда по таблице 1 общее решение уравнения  имеет вид:
имеет вид: 
Число 0 не корень характеристического уравнения, имеем случай 1. а) из таблицы 2
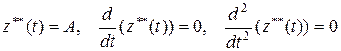 .
.
Подставляем в  , получим
, получим  , отсюда
, отсюда  ,
,
т.е.  , тогда
, тогда
 .
.
Пример 4. [5]. Задание Д.8. Применение теоремы об изменении количества движения к исследованию движения механической системы.
Дифференциальное уравнение движения тела имеет вид (стр.181)
 .
.
Характеристическое уравнение  имеет корни
имеет корни  , поэтому общее решение соответствующего однородного уравнения будет
, поэтому общее решение соответствующего однородного уравнения будет  . Число 0 является корнем характеристического уравнения, тогда согласно таблице 2, 1 б) частное решение ищем в виде х**=Аt, дифференцируя, получим
. Число 0 является корнем характеристического уравнения, тогда согласно таблице 2, 1 б) частное решение ищем в виде х**=Аt, дифференцируя, получим
 , отсюда
, отсюда
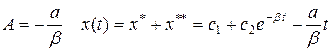 .
.
Из начальных условий  при t=0 можно найти с2
при t=0 можно найти с2
 отсюда
отсюда  .
.
Подставляя в  , получим
, получим  .
.
Пример 5 . [5]. Задание Д.3. Исследование колебательного движения материальной точки.
Дифференциальное уравнение имеет вид (стр.147) 
а)  .
.
Числа ±pi не являются корнями характеристического уравнения. По таблице 2, 3а) частное решение уравнения  ищем в виде
ищем в виде


Популярное:

