Уравнения с разделяющимися переменными
Наиболее простым дифференциальным уравнением первого порядка является уравнение вида
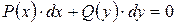 . (7)
. (7)
Такие уравнения называют уравнениями с разделёнными переменными. Проинтегрировав это уравнение почленно, получим
 (7*)
(7*)
– его общий интеграл.
Задача 3. Найти общий интеграл уравнения  .
.
Решение. Данное уравнение с разделенными переменными. Поэтому, 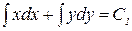 или
или 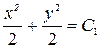 ,
, 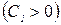 . Общий интеграл будет иметь вид:
. Общий интеграл будет иметь вид: 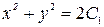 . Обозначив
. Обозначив 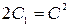 , получим
, получим 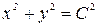 .
.
К уравнениям с разделёнными переменными сводятся дифференциальные уравнения с разделяющимися переменными
 (8)
(8)
путём почленного деления его на 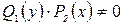 . Получаем
. Получаем 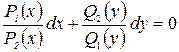 .
.
Общий интеграл:  . (8*)
. (8*)
Замечания.
1) В процессе почленного деления дифференциального уравнения (3) на 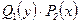 могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение
могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение 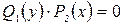 и найти те решения, которые не могут быть получены из общего решения.
и найти те решения, которые не могут быть получены из общего решения.
2) Уравнение вида  также сводится к уравнению с разделёнными переменными путём представления производной
также сводится к уравнению с разделёнными переменными путём представления производной 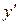 в виде
в виде  , т.е.
, т.е.  . Разделив переменные, получим
. Разделив переменные, получим  – это равенство двух дифференциалов и их неопределённые интегралы отличаются на постоянное число. Поэтому можно проинтегрировать левую часть по
– это равенство двух дифференциалов и их неопределённые интегралы отличаются на постоянное число. Поэтому можно проинтегрировать левую часть по  , а правую часть по
, а правую часть по  :
: 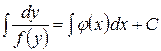 , где С – произвольная постоянная. После интегрирования получим общее решение дифференциального уравнения в явном виде или общий интеграл.
, где С – произвольная постоянная. После интегрирования получим общее решение дифференциального уравнения в явном виде или общий интеграл.
Задача 4. Найти общее решение дифференциального уравнения:
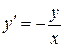 .
.
Решение: Полагая 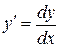 , перепишем данное уравнение в виде
, перепишем данное уравнение в виде 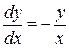 . Для разделения переменных умножим обе части на
. Для разделения переменных умножим обе части на 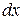 и разделим на
и разделим на  . Полученное уравнение
. Полученное уравнение 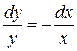 будет с разделёнными переменными, которое можно интегрировать:
будет с разделёнными переменными, которое можно интегрировать: 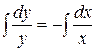 . Получаем общий интеграл
. Получаем общий интеграл  или
или 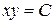 . (для удобства потенцирования постоянная интегрирования обозначена
. (для удобства потенцирования постоянная интегрирования обозначена 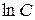 , что вполне допустимо, т.к.
, что вполне допустимо, т.к. 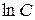 принимает значения от
принимает значения от 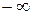 до
до 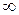 ). Общее решение данного дифференциального уравнения запишем в виде
). Общее решение данного дифференциального уравнения запишем в виде  .
.
При делении на  потеряно очевидное решение
потеряно очевидное решение  , что можно проверить непосредственной подстановкой в исходное уравнение.
, что можно проверить непосредственной подстановкой в исходное уравнение.
Проверка . Подставив функцию  и её производную
и её производную  в исходное дифференциальное уравнение, получим
в исходное дифференциальное уравнение, получим 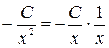 ,
, 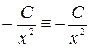 . Полученное тождество говорит о правильности решения уравнения.
. Полученное тождество говорит о правильности решения уравнения.
Задача 5. Проинтегрировать уравнение 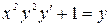 .
.
Решение. Полагая 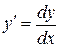 , перепишем данное уравнение в виде
, перепишем данное уравнение в виде 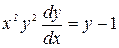 . Приведёмк виду с разделёнными переменными
. Приведёмк виду с разделёнными переменными 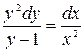 . Интегрируя обе части уравнения:
. Интегрируя обе части уравнения: 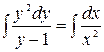 ,
, 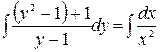 ,
, 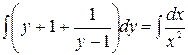 , получим
, получим  – общий интеграл.
– общий интеграл.
При делении на 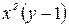 могли быть потеряны решения
могли быть потеряны решения  и
и  . Очевидно,
. Очевидно, 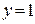 – решение данного дифференциального уравнения, а
– решение данного дифференциального уравнения, а  – нет.
– нет.
Задача 6. Найти частный интеграл дифференциального уравнение 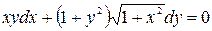 , удовлетворяющий начальному условию
, удовлетворяющий начальному условию  .
.
Решение. Приведём уравнение к виду с разделёнными переменными, разделив обе части на 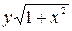 :
:  . Интегрируя
. Интегрируя 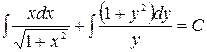 ,
, 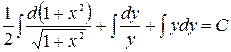 , получим общий интеграл
, получим общий интеграл  . Подставив в общий интеграл начальные данные
. Подставив в общий интеграл начальные данные 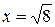 ,
, 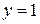 :
: 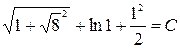 , найдём
, найдём 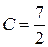 . Частный интеграл данного дифференциального уравнения примет вид:
. Частный интеграл данного дифференциального уравнения примет вид: 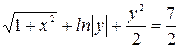 или
или 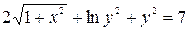 .
.
Задачи для самостоятельного решения:
1. Найти общий интеграл или общее решение дифференциальных уравнений:
1)  ; 2)
; 2) 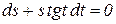 ;
;
3)  ; 4)
; 4) 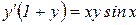
5)  ; 6)
; 6) 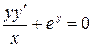
7) 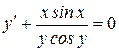 ; 8)
; 8) 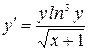
9)  ; 10)
; 10) 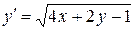
Ответы: 1) 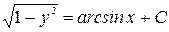 ; 2)
; 2) 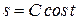 ; 3)
; 3) 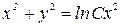 ; 4)
; 4) 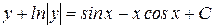 ; 5)
; 5) 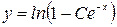 ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ; 9)
; 9) 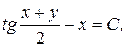
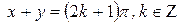 ; 10)
; 10) 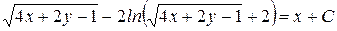 .
.
2. Найти частный интеграл или частные решения дифференциальных
уравнений:
1)  ,
, 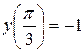 ; 2)
; 2)  ,
, 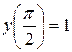 ;
;
3) 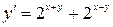 ,
, 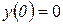 ; 4)
; 4) 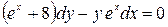 ,
,  .
.
Ответы: 1) 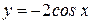 ; 2)
; 2) 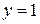 ; 3)
; 3)  ; 4)
; 4) 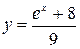 .
.
Однородные уравнения
Функция 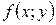 называется однородной функцией своих аргументов степени n, если выполняется тождество:
называется однородной функцией своих аргументов степени n, если выполняется тождество:
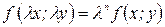 . (9)
. (9)
Например, функция 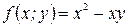 есть однородная функция 2-ой степени однородности, так как
есть однородная функция 2-ой степени однородности, так как 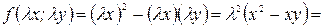

Функция 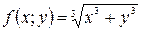 – однородная функция 1-ой степени однородности, т.к.
– однородная функция 1-ой степени однородности, т.к.  .
.
При 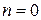 имеем функцию нулевой степени однородности
имеем функцию нулевой степени однородности 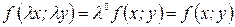 . Например,
. Например,  – однородная функция нулевой степени однородности, так как
– однородная функция нулевой степени однородности, так как 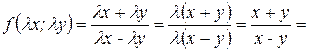
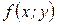 .
.
Дифференциальное уравнение вида
 (10)
(10)
называется однородным относительно x и y, если 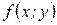 – функция нулевой степени однородности.
– функция нулевой степени однородности.
Уравнения (10) всегда можно представить в виде:
 . (11)
. (11)
Вводя новую искомую функцию  или
или 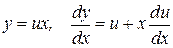 , уравнение (11) запишется в виде
, уравнение (11) запишется в виде 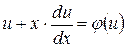 , которое сводится к уравнению с разделяющимися переменными
, которое сводится к уравнению с разделяющимися переменными 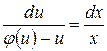 . Интегрируя это уравнение, находим
. Интегрируя это уравнение, находим 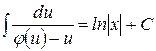 . Подставив вместо
. Подставив вместо 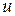
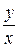 , получим общий интеграл уравнения (11). Если при каком-либо значении
, получим общий интеграл уравнения (11). Если при каком-либо значении 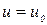 выполняется равенство
выполняется равенство  , то решения будут
, то решения будут 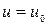 или
или  ,
, 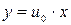 (прямые, проходящие через начало координат).
(прямые, проходящие через начало координат).
Задача 7. Решить уравнение 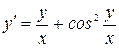 .
.
Решение: уравнение однородное относительно  и
и  вида (11). Вводим новую неизвестную функцию
вида (11). Вводим новую неизвестную функцию 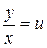 ,
, 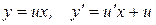 . Подставляя в данное дифференциальное уравнение, получаем:
. Подставляя в данное дифференциальное уравнение, получаем: 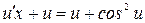 или
или  . Разделяем переменные и интегрируем
. Разделяем переменные и интегрируем 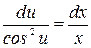 ,
, 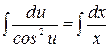 ,
,  ,
, 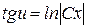 . Но
. Но  , поэтому
, поэтому 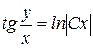 – общий интеграл. Можно найти и общее решение
– общий интеграл. Можно найти и общее решение  .
.
При 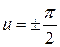
 , тогда к полученным решениям добавляются ещё два решения
, тогда к полученным решениям добавляются ещё два решения  , что проверяется подстановкой в исходное уравнение.
, что проверяется подстановкой в исходное уравнение.
Если в уравнении
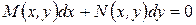 (12)
(12)
функции 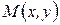 и
и  одной степени однородности, то их отношение
одной степени однородности, то их отношение 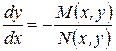 является функцией нулевой степени однородности, следовательно, уравнение будет однородным. Иногда уравнение (12) не приводят к виду (11) разрешенному относительно производной, а непосредственно в уравнении (12) делают подстановку
является функцией нулевой степени однородности, следовательно, уравнение будет однородным. Иногда уравнение (12) не приводят к виду (11) разрешенному относительно производной, а непосредственно в уравнении (12) делают подстановку 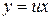 ,
,  , которая приводит к уравнению с разделяющимися переменными.
, которая приводит к уравнению с разделяющимися переменными.
Задача 8. Найти общий интеграл уравнения  .
.
Решение: Это уравнение однородное, так как функции  и
и  одной степени однородности. Разрешив уравнение относительно производной
одной степени однородности. Разрешив уравнение относительно производной  , получили в правой части функцию нулевой степени однородности. Вводя новую неизвестную функцию
, получили в правой части функцию нулевой степени однородности. Вводя новую неизвестную функцию 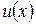 подстановкой
подстановкой 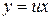 ,
, 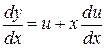 , получаем:
, получаем: 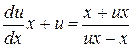 ,
, 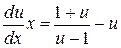 ,
, 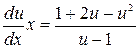 .
.
Разделим переменные 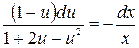 ,
, 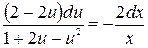 и проинтегрируем
и проинтегрируем 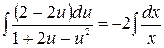 ,
,  (С > 0) или
(С > 0) или  . Но
. Но  , поэтому
, поэтому  или при делении на
или при делении на 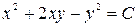 . Получили общий интеграл исходного уравнения. При делении на
. Получили общий интеграл исходного уравнения. При делении на  могли потерять решения
могли потерять решения  , то есть
, то есть  . Так как
. Так как  , имеем два решения
, имеем два решения  ,
, 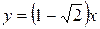 .
.
В данном случае эти решения получаются из общего интеграла при С = 0.
Задачи для самостоятельного решения:
1. Проинтегрировать следующие дифференциальные уравнения:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 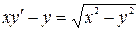 .
.
Ответы: 1)  ; 2)
; 2)  ; 3)
; 3) 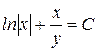 ; 4)
; 4) 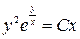 ; 5)
; 5) 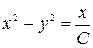 ; 6)
; 6) 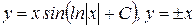 .
.
2. Найти частные решения дифференциальных уравнений
1) 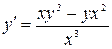 ,
, 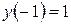 ; 2)
; 2)  ;
;  ;
;
3) 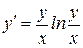 ,
, 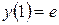 .
.
Ответы: 1)  ; 2)
; 2) 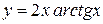 ; 3)
; 3) 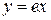 .
.
Линейные уравнения
Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Оно имеет вид:
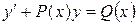 , (13)
, (13)
где  и
и  – заданные непрерывные функции в области интегрирования. (Если
– заданные непрерывные функции в области интегрирования. (Если  =0, то уравнение
=0, то уравнение 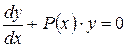 называется соответствующим однородным).
называется соответствующим однородным).
Линейные уравнения первого порядка (13) можно решить:
1) методом Бернулли: подстановка 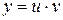 ,
, 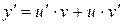 ;
;
2) методом Лагранжа: метод вариации произвольной постоянной.
1. Метод Бернулли
Будем искать решение исходного линейного уравнения (13) в виде произведения двух функций  , где
, где 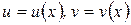 – неизвестные функции от x, причём одна из них произвольна, но не равна нулю. Тогда
– неизвестные функции от x, причём одна из них произвольна, но не равна нулю. Тогда 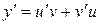 . Подставляя
. Подставляя  и
и 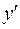 в уравнение (13), получим:
в уравнение (13), получим:
 или
или 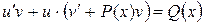 . (14)
. (14)
Выберем функцию v(x) так, чтобы выражение в скобках было равно нулю, т.е. 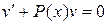 или
или 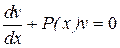 . Разделяя переменные и интегрируя, получим
. Разделяя переменные и интегрируя, получим 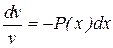 ,
,  .
.
Ввиду свободы выбора функции 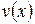 , можно принять С = 1. Следовательно,
, можно принять С = 1. Следовательно, 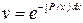 . Подставляя найденную функцию в уравнение (14), где
. Подставляя найденную функцию в уравнение (14), где 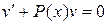 , имеем
, имеем 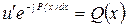 .
.
Это уравнение с разделяющимися переменными, решая которое, найдём функцию 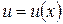 :
: 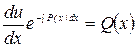 ,
, 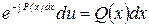 ,
, 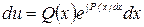
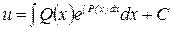
Следовательно, общим решением уравнения (13) будет
 .
.
2. Метод Лагранжа (метод вариации произвольной постоянной)
Найдём общее решение соответствующего однородного уравнения
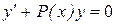 . (15)
. (15)
Разделяя переменные и интегрируя, находим последовательно:
 ,
,  ,
, 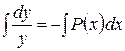 , откуда
, откуда 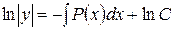 или
или 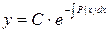 , где С – произвольная постоянная.
, где С – произвольная постоянная.
Варьируя произвольную постоянную, будем рассматривать С = С(х) как неизвестную дифференцируемую функцию. Общее решение неоднородного линейного уравнения (13) ищется в виде
 (16)
(16)
было решением неоднородного линейного уравнения.
Для нахождения С(х) подставляем  , т.е. функцию (16), и её производную
, т.е. функцию (16), и её производную 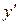 в исходное уравнение (13). Искомое решение будет иметь
в исходное уравнение (13). Искомое решение будет иметь
вид (16) после подстановки найденной функции С(х).
Задача 9. Решить уравнение: 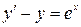 .
.
1 способ ( Метод Бернулли): Пусть 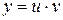 ,
, 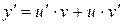 , тогда
, тогда 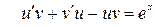 или
или  . Далее выбираем функцию
. Далее выбираем функцию 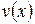 так, чтобы выражение в скобках обращалось в «0»
так, чтобы выражение в скобках обращалось в «0» 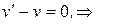
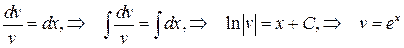 при С = 0, так как достаточно одного любого частного решения.
при С = 0, так как достаточно одного любого частного решения.
Подставив найденное  в уравнение
в уравнение  ,
, 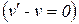 , получим
, получим 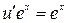 или
или 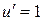 ,
, 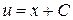 . Окончательно, общее решение исходного дифференциального уравнения
. Окончательно, общее решение исходного дифференциального уравнения 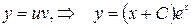 .
.
Проверка.  ,
, 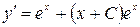 . Подставляем
. Подставляем  и
и 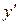 в исходное уравнение. Получаем тождество 1 = 1.
в исходное уравнение. Получаем тождество 1 = 1.
2 способ (Метод Лагранжа): Рассмотрим соответствующее однородное уравнение 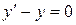 . Разделив переменные, проинтегрируем
. Разделив переменные, проинтегрируем 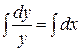 ,
,  . Заменив константу С неизвестной функцией
. Заменив константу С неизвестной функцией 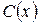 , решение исходного уравнения будем искать в виде
, решение исходного уравнения будем искать в виде 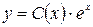 ,
,  . Подставив правые части этих равенств в исходное дифференциальное уравнение, получим:
. Подставив правые части этих равенств в исходное дифференциальное уравнение, получим: 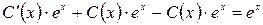 , откуда
, откуда 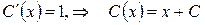 . Общее решение:
. Общее решение:  .
.
Задача 10. Проинтегрировать уравнение 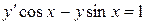 методом вариации постоянной при начальном условии
методом вариации постоянной при начальном условии 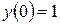 .
.
Решение. Запишем соответствующееоднородное уравнение
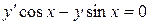 .
.
Разделив переменные: 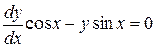 ,
, 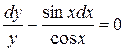 , интегрируем
, интегрируем 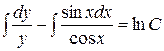 ,
, 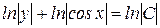 ,
, 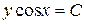 . Общее решение однородного уравнения будет иметь вид
. Общее решение однородного уравнения будет иметь вид 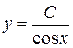 .
.
Решение исходного неоднородного уравнения будем искать в виде 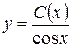 , где С(х) – неизвестная функция. Подставляя в исходное уравнение
, где С(х) – неизвестная функция. Подставляя в исходное уравнение 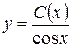 и
и 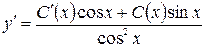 , получим
, получим
 ,
,
откуда 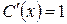 . Интегрируя, найдём
. Интегрируя, найдём  , где С – постоянная. Таким образом, получаем общее решение исходного уравнения
, где С – постоянная. Таким образом, получаем общее решение исходного уравнения 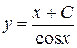 . Используя начальное условие
. Используя начальное условие 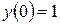 , найдём постоянную С:
, найдём постоянную С:  , откуда С = 1. Следовательно, искомое частное решение будет
, откуда С = 1. Следовательно, искомое частное решение будет 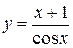 .
.
Задача 11. Методом Бернулли решить задачу Коши 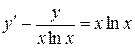 ,
,  .
.
Решение. Пусть 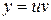 ,
, 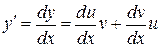 . Подставим
. Подставим  и
и 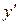 в исходное уравнение
в исходное уравнение 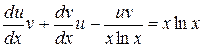 или
или 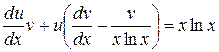 .
.
Выберем функцию 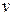 так, чтобы выражение в скобках было равно нулю:
так, чтобы выражение в скобках было равно нулю: 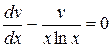 . Разделяя переменные и интегрируя, получаем
. Разделяя переменные и интегрируя, получаем 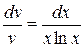 ,
,  ,
, 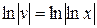 при С = 0. Отсюда
при С = 0. Отсюда 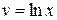 . Подставим функцию
. Подставим функцию 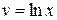 в уравнение
в уравнение 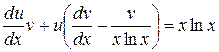 , получим
, получим 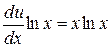 , т.е.
, т.е. 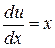 ,
, 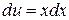 ,
,  ,
,  . Общее решение исходного линейного дифференциального уравнения будет иметь вид:
. Общее решение исходного линейного дифференциального уравнения будет иметь вид:
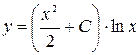 .
.
Используя начальные значения 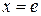 ,
, 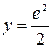 , найдём постоянную С:
, найдём постоянную С: 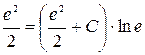 , откуда С = 0. Следовательно, искомое частное решение получим из общего решения при С = 0:
, откуда С = 0. Следовательно, искомое частное решение получим из общего решения при С = 0: 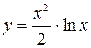 .
.
Приведём примеры приложения теории дифференциальных уравнений рассмотренного вида к решению задач из курса механики.
Задача 12.( [5] Задание Д.18, стр.266, 272. Применение теорем и принципов динамики к исследованию движения механической системы.)
Вращающий момент М(t), развиваемый электродвигателем, определяется дифференциальным уравнением 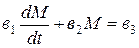 . Найти зависимость М(t) от времени, если М(0)=0.
. Найти зависимость М(t) от времени, если М(0)=0.
Решение. Так как данное дифференциальное уравнение является линейным первого порядка, то его решение можно найти в виде М(t)=u(t) × u(t) = u× u, следовательно, имеем 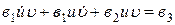 .
.
Выберем функцию u такой, чтобы 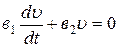 . Разделяем переменные
. Разделяем переменные 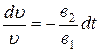 . После интегрирования получим
. После интегрирования получим 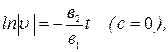 отсюда
отсюда 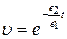 . Подставив
. Подставив 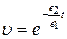 в уравнение
в уравнение 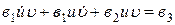 , где
, где 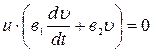 получим
получим  , отсюда следует
, отсюда следует 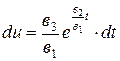 . Интегрируя последнее, находим
. Интегрируя последнее, находим 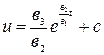 .
.
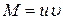 ,
,  ,
,  – общее решение уравнения. Подставляя начальные значения М=0 при t=0 в общее решение дифференциального уравнения, найдем постоянную интегрирования
– общее решение уравнения. Подставляя начальные значения М=0 при t=0 в общее решение дифференциального уравнения, найдем постоянную интегрирования  Таким образом, частное решение дифференциального уравнения будет иметь вид:
Таким образом, частное решение дифференциального уравнения будет иметь вид: 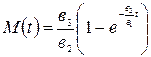 .
.
Задачи для самостоятельного решения:
1. Проинтегрировать следующие дифференциальные уравнения:
1)  ; 2)
; 2) 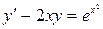 ; 3)
; 3)  ; 4)
; 4) 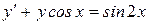 ; 5)
; 5) 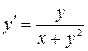 (Указание. Записать уравнение в виде
(Указание. Записать уравнение в виде  – линейно относительно
– линейно относительно  и
и 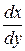 ).
).
Ответы: 1) 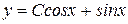 ; 2)
; 2)  ; 3)
; 3) 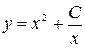 ; 4)
; 4)  ; 5)
; 5) 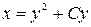 ,
,  – очевидное решение.
– очевидное решение.
2. Найти частные решения дифференциальных уравнений
1) 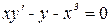 ,
, 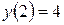 ; 2)
; 2) 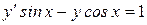 ,
, 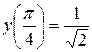 ;
;
3) 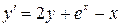 ,
,  .
.
Ответы: 1) 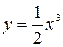 ; 2)
; 2) 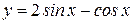 ; 3)
; 3) 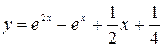 .
.
Лекция: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ
ПОРЯДКОВ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Основные понятия
Дифференциальные уравнения порядка выше первого называются дифференциальными уравнениями высших порядков. В общем случае дифференциальное уравнение n-ого порядка записывается в виде
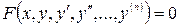 , (17)
, (17)
где  – аргумент,
– аргумент,  – искомая функция.
– искомая функция.
Если это возможно, уравнение (17) можно представить в виде, разрешённом относительно производной высшего порядка:
 . (18)
. (18)
Для таких уравнений имеет место теорема о существовании и единственности решения.
Задача нахождения решения 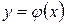 уравнения (18), которое при фиксированном (заданном) значении
уравнения (18), которое при фиксированном (заданном) значении  принимает заданные значения
принимает заданные значения 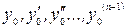 , т.е. удовлетворяют начальным условиям
, т.е. удовлетворяют начальным условиям
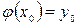 ,
,  ,
, 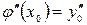 , …,
, …, 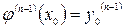 (19)
(19)
называется задачей Коши.
Теорема существования и единственности решения задачи Коши
Если в уравнении (18) функция  непрерывна по всем аргументам в области D их изменения и имеет ограниченные частные производные по аргументам
непрерывна по всем аргументам в области D их изменения и имеет ограниченные частные производные по аргументам 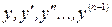 , то существует единственное решение
, то существует единственное решение 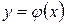 уравнения (18) определённое и непрерывное в некотором интервале, содержащем
уравнения (18) определённое и непрерывное в некотором интервале, содержащем  и удовлетворяющее системе начальных условий (19), где значения
и удовлетворяющее системе начальных условий (19), где значения 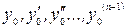 содержатся в области D.
содержатся в области D.
Для уравнения второго порядка  начальными условиями будут
начальными условиями будут 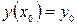 ,
,  , где
, где  – заданные числа. Тогда геометрически теорема существования и единственности решения задачи Коши означает, что через заданную точку
– заданные числа. Тогда геометрически теорема существования и единственности решения задачи Коши означает, что через заданную точку 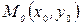 области D с заданным тангенсом угла наклона касательной
области D с заданным тангенсом угла наклона касательной  проходит единственная интегральная кривая (в механике означает задание точки и задание скорости в этой точке).
проходит единственная интегральная кривая (в механике означает задание точки и задание скорости в этой точке).
Общим решением дифференциального уравнения n-ого порядка (18) называется множество его решений вида 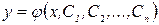 , где
, где  произвольные постоянные интегрирования.
произвольные постоянные интегрирования.
Частным решением уравнения (18) называется решение, полученное из общего решения при конкретных значениях произвольных постоянных  (в частности, всякое решение задачи Коши). Поэтому часто произвольные постоянные находят из условий задачи Коши однозначно при фиксированном
(в частности, всякое решение задачи Коши). Поэтому часто произвольные постоянные находят из условий задачи Коши однозначно при фиксированном  .
.
Общим интегралом уравнения (18) называется соотношение  , содержащее неявно общее решение
, содержащее неявно общее решение 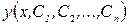 . Придавая постоянным
. Придавая постоянным  конкретные допустимые числовые значения, получим частный интеграл дифференциального уравнения.
конкретные допустимые числовые значения, получим частный интеграл дифференциального уравнения.
Рассмотрим некоторые виды дифференциальных уравнений, допускающих понижение порядка.
Популярное:

