Проверка статистических гипотез о значениях коэффициентов
В только что рассмотренном примере мы построили  – доверительный интервал для параметра
– доверительный интервал для параметра 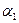 в виде
в виде

т. е.

Существенно, что при любом истинном значении параметра 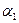 вероятность накрытия этого значения построенным доверительным интервалом равна
вероятность накрытия этого значения построенным доверительным интервалом равна  .
.
Рассмотрим значение 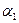 =1; построенный интервал его не накрывает. Однако, если
=1; построенный интервал его не накрывает. Однако, если 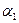 действительно равняется 1, то вероятность такого ненакрытия равна
действительно равняется 1, то вероятность такого ненакрытия равна  . Таким образом, факт ненакрытия значения
. Таким образом, факт ненакрытия значения 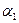 =1 построенным интервалом представляет (в случае, когда
=1 построенным интервалом представляет (в случае, когда 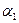 =1) осуществление довольно редкого события, имеющего малую вероятность
=1) осуществление довольно редкого события, имеющего малую вероятность  , и это дает нам основания сомневаться в том, что в действительности
, и это дает нам основания сомневаться в том, что в действительности 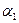 =1.
=1.
То же самое относится и к любому другому фиксированному значению  , не принадлежащему указанному
, не принадлежащему указанному  -доверительному интервалу: предположение о том, что в действительности
-доверительному интервалу: предположение о том, что в действительности  , представляется маловероятным.
, представляется маловероятным.
Подобного рода предположения называют в этом контексте статистическими гипотезами (statistical hypothesis). О проверяемой гипотезе говорят как об исходной – «нулевой» (maintained, null) гипотезе и обозначают такую гипотезу символом  , так что в последнем случае мы имеем дело с гипотезой
, так что в последнем случае мы имеем дело с гипотезой

В соответствии со сказанным выше, такую гипотезу естественно отвергать (отклонять), если значение  не принадлежит
не принадлежит  -доверительному интервалу для
-доверительному интервалу для 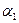 , т. е. интервалу
, т. е. интервалу

Вспоминая, как этот интервал строился, мы замечаем, что  непринадлежит этому интервалу тогда и только тогда, когда
непринадлежит этому интервалу тогда и только тогда, когда

т. е. когда наблюдаемое значение отношения
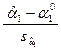
«слишком велико» по абсолютной величине. Последнее означает «слишком большое» отклонение оценки 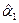 от гипотетического значения
от гипотетического значения  параметра
параметра 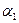 , в сравнении с оценкой
, в сравнении с оценкой 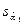 значения
значения  корня из дисперсии оценки этого параметра.
корня из дисперсии оценки этого параметра.
Итак, если

мы отвергаем гипотезу  . Однако выполнение этого неравенства для некоторого значения
. Однако выполнение этого неравенства для некоторого значения  вовсе не означает, что гипотеза
вовсе не означает, что гипотеза  обязательно не верна. Если в действительности
обязательно не верна. Если в действительности  , то все же имеется вероятность
, то все же имеется вероятность  того, что это неравенство будет выполнено.
того, что это неравенство будет выполнено.
В последнем случае, в соответствии с выбранным правилом, мы все же отвергнем гипотезу  , допустив при этом «ошибку 1-го рода». Такая ошибка происходит в среднем в
, допустив при этом «ошибку 1-го рода». Такая ошибка происходит в среднем в  случаях из ста.
случаях из ста.
Если бы мы выбрали произвольный доверительный уровень  , то тогда мы отвергали бы гипотезу
, то тогда мы отвергали бы гипотезу  при выполнении неравенства
при выполнении неравенства

и ошибка 1-го рода происходила в среднем в 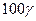 случаев из
случаев из  . Точнее, вероятность ошибки 1-го рода была бы равна
. Точнее, вероятность ошибки 1-го рода была бы равна 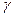 :
:

 отвергается
отвергается 
 верна
верна 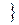 =
= 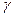 .
.
Само правило решения вопроса об отклонении или неотклонении статистической гипотезы  называется статистическим критерием проверки гипотезы Н0, а выбранное при формулировании этого правила значение g называется уровнем значимости критерия.
называется статистическим критерием проверки гипотезы Н0, а выбранное при формулировании этого правила значение g называется уровнем значимости критерия.
Выбор большего или меньшего значения g определяется степенью значимости для исследователя исходной гипотезы  . Скажем, выбор между значениями
. Скажем, выбор между значениями 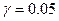 и
и  в пользу
в пользу  означает, что исследователь заранее настроен в пользу гипотезы
означает, что исследователь заранее настроен в пользу гипотезы  и ему требуются очень весомые аргументы, свидетельствующие против этой гипотезы, чтобы все же отказаться от нее. Выбор же в пользу уровня значимости
и ему требуются очень весомые аргументы, свидетельствующие против этой гипотезы, чтобы все же отказаться от нее. Выбор же в пользу уровня значимости 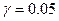 означает, что исследователь не столь сильно отстаивает гипотезу
означает, что исследователь не столь сильно отстаивает гипотезу  и готов отказаться от нее и при менее убедительной аргументации против этой гипотезы.
и готов отказаться от нее и при менее убедительной аргументации против этой гипотезы.
Всякий статистический критерий основывается на использовании той или иной статистики (статистики критерия), т. е. случайной величины, значения которой могут быть вычислены (по крайней мере, теоретически) на основании имеющихся статистических данных и распределение которой известно (хотя бы приближенно).
В нашем примере критерий проверки гипотезы  основывался на использовании t-статистики
основывался на использовании t-статистики
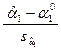 ,
,
значение которой можно вычислить по данным наблюдений, поскольку  – известное (заданное) число, а
– известное (заданное) число, а 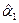 и
и  вычисляются на основании данных наблюдений.
вычисляются на основании данных наблюдений.
Каждому статистическому критерию соответствует критическое множество R значений статистики критерия, при которых гипотеза  отвергается в соответствии с принятым правилом. В нашем примере таковым является множество значений указанной
отвергается в соответствии с принятым правилом. В нашем примере таковым является множество значений указанной  -статистики, превышающих по абсолютной величине значение
-статистики, превышающих по абсолютной величине значение 
Итак, статистический критерий определяется заданием
a. статистической гипотезы Н 0;
b. уровня значимости g;
c. статистики критерия;
d. критического множества R.
Можно подумать, что пункты b) и d) дублируют друг друга, поскольку в нашем примере критическое множество 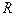 однозначно определяется по заданному уровню значимости
однозначно определяется по заданному уровню значимости 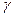 . Однако, как мы увидим в дальнейшем, одному и тому же уровню значимости можно сопоставить различные критические множества, что дает возможность выбирать множество
. Однако, как мы увидим в дальнейшем, одному и тому же уровню значимости можно сопоставить различные критические множества, что дает возможность выбирать множество 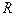 наиболее рациональным образом, в зависимости от выбора гипотезы
наиболее рациональным образом, в зависимости от выбора гипотезы 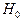 (выбор наиболее мощного критерия).
(выбор наиболее мощного критерия).
Компьютерные пакеты программ статистического анализа данных (в том числе и Пакет анализа EXСEL)первоочередное внимание уделяют проверке гипотезы

в рамках нормальной модели множественной линейной регрессии
у=a0+a1х1 +a2х2 +…+amхm+e.
где e нормально распределенная случайная величина с параметрами 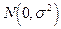 .
.
Эта гипотеза соответствует предположению исследователя о том, что  -я объясняющая переменная не имеет существенного значения с точки зрения объяснения изменчивости значений объясняемой переменной
-я объясняющая переменная не имеет существенного значения с точки зрения объяснения изменчивости значений объясняемой переменной  , так что она может быть исключена из модели.
, так что она может быть исключена из модели.
Для соответствующего критерия
a.  ;
;
b. уровень значимости 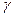 по умолчанию обычно выбирается равным
по умолчанию обычно выбирается равным  ;
;
c. статистика критерия имеет вид

если гипотеза  верна, то эта статистика имеет
верна, то эта статистика имеет  - распределение Стьюдента с
- распределение Стьюдента с  степенями свободы,
степенями свободы,
 ~
~  ,
,
в связи с чем ее обычно называют t-статистикой (t-statistic) или t-отношением (t-ratio);
d) критическое множество имеет вид

При этом, в распечатках результатов регрессионного анализа (т. е. статистического анализа модели линейной регрессии) сообщаются:
· значение оценки  параметра
параметра 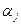 в графе Коэффициенты (Coefficient);
в графе Коэффициенты (Coefficient);
· значение 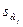 знаменателя t-статистики в графе Стандартная ошибка (Std. Error);
знаменателя t-статистики в графе Стандартная ошибка (Std. Error);
· значение отношения  в графе t-статистика (t-statistic).
в графе t-статистика (t-statistic).
Кроме того, сообщается также
· вероятность того, что случайная величина, имеющая распределение Стьюдента с 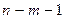 степенями свободы, примет значение, не меньшее по абсолютной величине, чем наблюденное значение
степенями свободы, примет значение, не меньшее по абсолютной величине, чем наблюденное значение  – в графе Р-значение (Р-value или Probability).
– в графе Р-значение (Р-value или Probability).
В отношении полученного при анализе Р-значения возможны следующие варианты.
Если указываемое P-значение меньше выбранного уровня значимости  , то это равносильно тому, что значение t-статистики
, то это равносильно тому, что значение t-статистики  попало в область отвержения гипотезы
попало в область отвержения гипотезы  , т. е.
, т. е.  В этом случае гипотеза
В этом случае гипотеза  отвергается.
отвергается.
Если указываемое P-значение больше выбранного уровня значимости 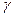 , то это равносильно тому, что значение t-статистики
, то это равносильно тому, что значение t-статистики  не попало в область отвержения гипотезы
не попало в область отвержения гипотезы  , т. е.
, т. е.  В этом случае гипотеза
В этом случае гипотеза  не отвергается.
не отвергается.
Если (в пределах округления) указываемое P-значение равно выбранному уровню значимости  , то в отношении гипотезы
, то в отношении гипотезы  можно принять любое из двух возможных решений.
можно принять любое из двух возможных решений.
В случае, когда гипотеза  отвергается (вариант 1), говорят, что параметр
отвергается (вариант 1), говорят, что параметр 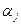 статистически значим (statistically significant); это соответствует признанию того, что наличие j-й объясняющей переменной в правой части модели существенно для объяснения наблюдаемой изменчивости объясняемой переменной.
статистически значим (statistically significant); это соответствует признанию того, что наличие j-й объясняющей переменной в правой части модели существенно для объяснения наблюдаемой изменчивости объясняемой переменной.
Напротив, в случае, когдагипотеза  не отвергается (вариант 2), говорят, что параметр
не отвергается (вариант 2), говорят, что параметр  статистически незначим (statistically unsignificant). В этом случае в рамках используемого статистического критерия мы не получаем убедительных аргументов против предположения о том, что
статистически незначим (statistically unsignificant). В этом случае в рамках используемого статистического критерия мы не получаем убедительных аргументов против предположения о том, что  . Это соответствует признанию того, что наличие j-й объясняющей переменной в правой части модели не существенно для объяснения наблюдаемой изменчивости объясняемой переменной, а следовательно, можно обойтись и без включения этой переменной в модель регрессии.
. Это соответствует признанию того, что наличие j-й объясняющей переменной в правой части модели не существенно для объяснения наблюдаемой изменчивости объясняемой переменной, а следовательно, можно обойтись и без включения этой переменной в модель регрессии.
Впрочем, выводы о статистической значимости (или незначимости) того или иного параметра модели зависят от выбранного уровня значимости  : решение в пользу статистической значимости параметра может измениться на противоположное при уменьшении
: решение в пользу статистической значимости параметра может измениться на противоположное при уменьшении 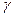 , а решение в пользу статистической незначимости параметра может измениться на противоположное при уменьшении значения
, а решение в пользу статистической незначимости параметра может измениться на противоположное при уменьшении значения 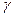 .
.
Пример. Пусть в примере с уровнями безработицы в США получаем  и следующую таблицу:
и следующую таблицу:
| Переменная
| Коэф-т
| Ст. ошибка
| t-статист.
| P-знач.
|
|
| 2.294
| 0.410
| 5.589
| 0.0001
|
| ZVET
| 0.125
| 0.062
| 2.011
| 0.0626
|
Соответственно, при выборе уровня значимости 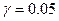 коэффициент при переменной
коэффициент при переменной  признается статистически незначимым (
признается статистически незначимым (  -значение больше уровня значимости). Однако, если выбрать
-значение больше уровня значимости). Однако, если выбрать  , то
, то  -значение меньше уровня значимости, и коэффициент при переменной
-значение меньше уровня значимости, и коэффициент при переменной  придется признать статистически значимым.
придется признать статистически значимым.
Пример. Пусть при исследовании зависимости спроса на куриные яйца от цены получаем  и следующую таблицу:
и следующую таблицу:
| Переменная
| Коэф-т
| Ст. ошибка
| t-статист.
| P-знач.
|
|
| 21.100
| 2.304
| 9.158
| 0.0000
|
| CENA
| –18.559
| 5.010
| -3.705
| 0.0026
|
Здесь коэффициент при объясняющей переменной  статистически значим даже при выборе
статистически значим даже при выборе  , так что цена является существенной объясняющей переменной.
, так что цена является существенной объясняющей переменной.
Пример. Регрессионный анализ потребления свинины на душу населения США в зависимости от оптовых цен на свинину дает значения  и
и
| Переменная
| Коэф-т
| Ст. ошибка
| t-статист.
| P-знач.
|
|
| 77.484
| 13.921
| 5.566
| 0.0001
|
| Цена
| -24.775
| 29.794
| -0.832
| 0.4219
|
В этом примере коэффициент при переменной Цена оказывается статистически незначимым при любом разумном выборе уровня значимости 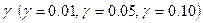 .
.
Замечание. Мы уже отмечали ранее возможность ложной корреляции между двумя переменными и, соответственно, возможность ложного использования одной из переменных в качестве объясняющей для описания изменчивости другой переменной. Проиллюстрируем такую ситуацию на основе рассмотренных нами методов регрессионного анализа.
Пример. Рассмотрим модель линейной связи между мировым рекордом по прыжкам в высоту с шестом среди мужчин (  , в см) и суммарным производством электроэнергии в США (
, в см) и суммарным производством электроэнергии в США (  , в млрд. квт-час). Пусть значение коэффициента детерминации для этой модели
, в млрд. квт-час). Пусть значение коэффициента детерминации для этой модели  . Результаты регрессионного анализа:
. Результаты регрессионного анализа:
| Переменная
| Коэф-т
| Ст. ошибка
| t-статист.
| P-знач.
|
|
| -2625.497
| 420.840
| -6.234
| 0.0000
|
| H
| 7.131
| 0.841
| 8.483
| 0.0000
|
Формально, переменная  признается существенной для объяснения изменчивости переменной
признается существенной для объяснения изменчивости переменной  , так что здесь мы сталкиваемся с ложной (паразитной) регрессией переменной
, так что здесь мы сталкиваемся с ложной (паразитной) регрессией переменной  на переменную
на переменную  , обусловленной наличием выраженного (линейного) тренда обеих переменных во времени.
, обусловленной наличием выраженного (линейного) тренда обеих переменных во времени.
5.3. Проверка значимости параметров линейной регрессии и подбор модели с использованием f-критериев
Приводимая ниже таблица содержит ежегодные данные о следующих показателях экономики Франции за период с 1949 по 1960 годы (млрд. франков, в ценах 1959 г.):
Y –объем импорта товаров и услуг во Францию;
X1 –валовой национальный продукт;
X2 –потребление семей.
| год
| Y
| X1
| X2
| год
| Y
| X1
| X2
|
|
| 15.9
| 149.3
| 4.2
|
| 22.7
| 202.1
| 2.1
|
|
| 16.4
| 161.2
| 4.1
|
| 26.5
| 212.4
| 5.6
|
|
| 19.0
| 171.5
| 3.1
|
| 28.1
| 226.1
| 5.0
|
|
| 19.1
| 175.5
| 3.1
|
| 27.6
| 231.9
| 5.1
|
|
| 18.8
| 180.8
| 1.1
|
| 26.3
|
| 0.7
|
|
| 20.4
| 190.7
| 2.2
|
| 31.1
|
| 5.6
|
Выберем модель наблюдений в виде

где  – значение показателя
– значение показателя  в i-м наблюдении (i-му наблюдению соответствует
в i-м наблюдении (i-му наблюдению соответствует 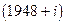 год. Будем, как обычно, предполагать что
год. Будем, как обычно, предполагать что  нормально распределенные случайные величины с параметрами
нормально распределенные случайные величины с параметрами  и что значение
и что значение  нам не известно. Регрессионный анализ дает следующие результаты:
нам не известно. Регрессионный анализ дает следующие результаты:  и
и
| Переменная
| Коэф-т
| Ст. ошибка
| t-статист.
| P-знач.
|
|
| –8.570
| 2.869
| -2.988
| 0.0153
|
| X1
| 0.029
| 0.110
| 0.267
| 0.7953
|
| X2
| 0.177
| 0.166
| 1.067
| 0.3136
|
Обращают на себя внимание выделенные курсивом  -значения. В соответствии с ними, проверка каждой отдельной гипотезы
-значения. В соответствии с ними, проверка каждой отдельной гипотезы  ,
,  (даже при уровне значимости
(даже при уровне значимости  ) приводит к решению о ее неотклонении. Соответственно, при реализации каждой из этих двух процедур проверки соответствующий параметр
) приводит к решению о ее неотклонении. Соответственно, при реализации каждой из этих двух процедур проверки соответствующий параметр  или
или 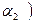 признается статистически незначимым. И это выглядит противоречащим весьма высокому значению коэффициента детерминации.
признается статистически незначимым. И это выглядит противоречащим весьма высокому значению коэффициента детерминации.
По-существу, вопрос стоит таким образом: необходимо построить статистическую процедуру для проверки гипотезы
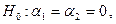
конкретизирующей значения не какого-то одного, а сразу двух коэффициентов.
И вообще, как проверить гипотезу
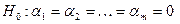
(гипотеза значимости регрессии) в рамках нормальной линейной модели множественной регрессии

Соответствующий статистический критерий основывается на так называемой F-статистике

Здесь  – остаточная сумма квадратов, получаемая при оценивании полной модели (с
– остаточная сумма квадратов, получаемая при оценивании полной модели (с  объясняющими переменными, включая тождественную единицу), а
объясняющими переменными, включая тождественную единицу), а 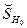 – остаточная сумма квадратов, получаемая при оценивании модели с наложенными гипотезой
– остаточная сумма квадратов, получаемая при оценивании модели с наложенными гипотезой  ограничениями на параметры. Но последняя (редуцированная) модель имеет вид
ограничениями на параметры. Но последняя (редуцированная) модель имеет вид

и применение к ней метода наименьших квадратов приводит к оценке
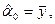
так что

Следовательно,

В некоторых пакетах статистического анализа (например, в EXCEL) в распечатках результатов приводятся значения числителя и знаменателя этой статистики (в графе Средние квадраты – Mean Squares).
Если  нормально распределенные случайные величины с параметрами
нормально распределенные случайные величины с параметрами  , то указанная
, то указанная  -статистика, рассматриваемая как случайная величина, имеет при гипотезе H0 (т. е. когда действительно α 1=¼ = α m= 0) стандартное распределение
-статистика, рассматриваемая как случайная величина, имеет при гипотезе H0 (т. е. когда действительно α 1=¼ = α m= 0) стандартное распределение  , называемое F-распределением Фишера с m и (n-m-1) степенями свободы.
, называемое F-распределением Фишера с m и (n-m-1) степенями свободы.
Чем больше отношение  , тем больше есть оснований говорить о том, что совокупность переменных
, тем больше есть оснований говорить о том, что совокупность переменных  действительно помогает в объяснении изменчивости объясняемой переменной
действительно помогает в объяснении изменчивости объясняемой переменной  .
.
В соответствии с этим, гипотеза
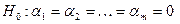
отвергается при «слишком больших» значениях F, скорее указывающих на невыполнение этой гипотезы. Соответствующее пороговое значение определяется как квантиль уровня  распределения
распределения  , обозначаемая символом
, обозначаемая символом 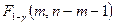 .
.
Итак, гипотеза Н0 отвергается, если выполняется неравенство
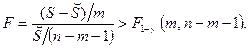
При этом вероятность ошибочного отвержения гипотезы  равна
равна 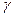 .
.
Статистические пакеты, выполняющие регрессионный анализ, приводят среди прочих результатов такого анализа также значение  указанной
указанной  -статистики и соответствующее ему P-значение (P-value), т. е. вероятность
-статистики и соответствующее ему P-значение (P-value), т. е. вероятность

В частности, в рассмотренном выше примере с импортом товаров и услуг во Францию вычисленное (наблюдаемое) значение  -статистики равно
-статистики равно  , в то время как критическое значение
, в то время как критическое значение

Соответственно,  -значение крайне мало – в распечатке результатов приведено значение
-значение крайне мало – в распечатке результатов приведено значение  . Значит, здесь нет практически никаких оснований принимать составную гипотезу
. Значит, здесь нет практически никаких оснований принимать составную гипотезу  , хотя каждая из частных гипотез
, хотя каждая из частных гипотез
 и
и  ,
,
рассматриваемая сама по себе, в отрыве от второй, не отвергается.
Подобное положение встречается не так уж и редко и связано с проблемой мультиколлинеарности данных. Далее мы уделим этой проблеме определенное внимание.
Пример. Анализ данныхоб уровнях безработицы среди белого и цветного населения США приводит к следующим результатам:
 ,
,  ,
,  -значение =
-значение =  , так что при выборе
, так что при выборе 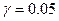 гипотеза
гипотеза  не отвергается, а при выборе
не отвергается, а при выборе  отвергается.
отвергается.
Пример. Анализ зависимости спроса на куриные яйца от цены приводит к значениям
 ,
,  ,
,  -значение =
-значение =  , так что гипотеза
, так что гипотеза  отвергается, а регрессия признается статистически значимой.
отвергается, а регрессия признается статистически значимой.
Пример. Зависимость производства электроэнергии в США от мирового рекорда по прыжкам в высоту с шестом:
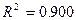 ,
,  ,
,  -значение =
-значение =  , регрессия признается статистически значимой.
, регрессия признается статистически значимой.
Пример. Потребление свинины в США в зависимости от оптовых цен:
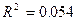 ,
,  ,
,  -значение =
-значение =  , так что гипотеза
, так что гипотеза  не отвергается даже при выборе
не отвергается даже при выборе  .
.
Отметим, наконец, еще одно обстоятельство. Во всех четырех рассмотренных примерах регрессионного анализа модели простой (парной) линейной регрессии (m=1) вычисленные  -значения
-значения  -статистик совпадают с
-статистик совпадают с  -значениями
-значениями  -статистик, используемых для проверки гипотезы
-статистик, используемых для проверки гипотезы  . Факт такого совпадения отнюдь не случаен и может быть доказан с использованием алгебраических преобразований.
. Факт такого совпадения отнюдь не случаен и может быть доказан с использованием алгебраических преобразований.
Применение критериев, основанных на статистиках, имеющих при нулевой гипотезе  -распределение Фишера (F-критерии), отнюдь не ограничивается только что рассмотренным анализом статистической значимости регрессии. Такие критерии широко применяются в процессе подбора модели.
-распределение Фишера (F-критерии), отнюдь не ограничивается только что рассмотренным анализом статистической значимости регрессии. Такие критерии широко применяются в процессе подбора модели.
Пусть мы находимся в рамках множественной линейной модели регрессии

c  объясняющими переменными, и гипотеза
объясняющими переменными, и гипотеза  состоит в том, что в модели
состоит в том, что в модели  последние
последние 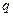 коэффициентов равны нулю, т. е.
коэффициентов равны нулю, т. е.

Тогда при гипотезе  (т. е. в случае, когда она верна) мы имеем редуцированную модель
(т. е. в случае, когда она верна) мы имеем редуцированную модель

уже с  объясняющими переменными.
объясняющими переменными.
Пусть  - остаточная сумма квадратов в полной модели
- остаточная сумма квадратов в полной модели  , а
, а 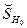 – остаточная сумма квадратов в редуцированной модели
– остаточная сумма квадратов в редуцированной модели  . Если гипотеза
. Если гипотеза  верна и выполнены стандартные предположения о модели (в частности,
верна и выполнены стандартные предположения о модели (в частности,  нормально распределенные случайные величины с параметрами
нормально распределенные случайные величины с параметрами  ), то тогда F-статистика
), то тогда F-статистика
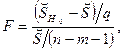
рассматриваемая как случайная величина, имеет при гипотезе H0 (т. е. когда действительно α m = α m-1= ¼ = α m-q+1= 0) F-распределение Фишера F (q, n-m-1) с q и (n-m-1) степенями свободы.
F-статистика измеряет, в соответствующем масштабе, возрастание объясненной суммы квадратов вследствие включения в модель дополнительного количества объясняющих переменных.
Естественно считать, что включение дополнительных переменных существенно, если указанное возрастание объясненной суммы квадратов достаточно велико. Это приводит нас к критерию проверки гипотезы

основанному на F-статистике и отвергающему гипотезу  , когда наблюдаемое значение
, когда наблюдаемое значение  этой статистики удовлетворяет неравенству
этой статистики удовлетворяет неравенству

где 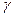 – выбранный уровень значимости критерия (вероятность ошибки 1-го рода).
– выбранный уровень значимости критерия (вероятность ошибки 1-го рода).
Пример. В следующей таблице приведены данные по США о следующих макроэкономических показателях:
 –годовой совокупный располагаемый личный доход;
–годовой совокупный располагаемый личный доход;
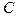 –годовые совокупные потребительские расходы;
–годовые совокупные потребительские расходы;
 –финансовые активы населения на начало календарного года
–финансовые активы населения на начало календарного года
(все показатели указаны в млрд. долларов, в ценах 1982 г.).
| год
| C82
| DPI82
| A82
|
| 1540.3
| 1730.1
| 1902.8
|
|
| 1300.5
| 1433.0
| 1641.6
|
| 1622.3
| 1797.9
| 2011.4
|
|
| 1339.4
| 1494.9
| 1675.2
|
| 1687.9
| 1914.9
| 2190.6
|
|
| 1405.9
| 1551.1
| 1772.6
|
| 1672.4
| 1894.9
| 2301.8
|
|
| 1458.3
| 1601.7
| 1854.7
|
| 1710.8
| 1930.4
| 2279.6
|
|
| 1491.8
| 1668.1
| 1862.2
|
| 1804.0
| 2001.0
| 2308.4
|
Рассмотрим модель наблюдений
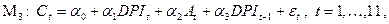
где индексу  соответствует
соответствует  год. Это модель с 3 объясняющими переменными:
год. Это модель с 3 объясняющими переменными:

символ  обозначает переменную, значения которой запаздывают на одну единицу времени относительно значений переменной,
обозначает переменную, значения которой запаздывают на одну единицу времени относительно значений переменной,  . Оценивание этой модели дает следующие результаты:
. Оценивание этой модели дает следующие результаты:


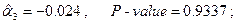


 — статистика критерия проверки значимости регрессии в целом
— статистика критерия проверки значимости регрессии в целом

Регрессия имеет очень высокую статистическую значимость. Вместе с тем, каждый из коэффициентов при двух последних переменных статистически незначим, так что, в частности, не следует придавать особого значения отрицательности оценок этих коэффициентов.
Используя  – критерий, мы могли бы попробовать удалить из модели какую-нибудь одну из двух последних переменных, и если оставшиеся переменные окажутся значимыми, то остановиться на модели с 2 объясняющими переменными; если же и в новой модели окажутся статистически незначимые переменные, то произвести еще одну редукцию модели.
– критерий, мы могли бы попробовать удалить из модели какую-нибудь одну из двух последних переменных, и если оставшиеся переменные окажутся значимыми, то остановиться на модели с 2 объясняющими переменными; если же и в новой модели окажутся статистически незначимые переменные, то произвести еще одну редукцию модели.
Рассмотрим, в этой связи, модель

с удаленной переменной  . Для нее получаем:
. Для нее получаем:




F-статистика критерия проверки значимости регрессии в этой модели

Поскольку здесь остается статистически незначимым коэффициент при переменной  , можно произвести дальнейшую редукцию, переходя к модели
, можно произвести дальнейшую редукцию, переходя к модели

Для этой модели



 -статистика критерия проверки значимости регрессии в этой модели
-статистика критерия проверки значимости регрессии в этой модели

и эту модель в данном контексте можно принять за окончательную.
С другой стороны, обнаружив при анализе модели  (посредством применения t-критериев) статистическую незначимость коэффициентов при двух последних переменных, мы можем попробовать выяснить возможность одновременного исключения из этой модели указанных объясняющих переменных, опираясь на использование соответствующего F-критерия.
(посредством применения t-критериев) статистическую незначимость коэффициентов при двух последних переменных, мы можем попробовать выяснить возможность одновременного исключения из этой модели указанных объясняющих переменных, опираясь на использование соответствующего F-критерия.
Исключение двух последних переменных из модели  соответствует гипотезе
соответствует гипотезе
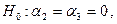
при которой модель  редуцируется сразу к модели
редуцируется сразу к модели  . Критерий проверки гипотезы
. Критерий проверки гипотезы  основывается на статистике
основывается на статистике
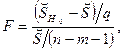
где  – остаточная сумма квадратов в модели
– остаточная сумма квадратов в модели  ,
, 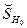 – остаточная сумма квадратов в модели
– остаточная сумма квадратов в модели  ,
, 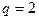 – количество зануляемых параметров,
– количество зануляемых параметров,  .
.
Для наших данных получаем значение

которое следует сравнить с критическим значением  Поскольку
Поскольку  , мы не отвергаем гипотезу
, мы не отвергаем гипотезу 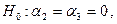 и можем сразу перейти от модели
и можем сразу перейти от модели  к модели
к модели  .
.
Замечание. В рассмотренном примере мы действовали двумя способами:
Популярное:

