
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Эффект Джоуля-Томсона. Сжижение газов. Фазовые переходы 1-го и 2-го рода. ⇐ ПредыдущаяСтр 4 из 4
Эффектом Джоуля — Томсона называется изменение температуры газа при адиабатическом дросселировании — медленном протекании газа под действием постоянного перепада давлений сквозь дроссель (пористую перегородку). Данный эффект является одним из методов получения низких температур. Изменение температуры при малом изменении давления (дифференциальный эффект) в результате процесса Джоуля — Томсона определяется производной
где Если при протекании газа через пористую перегородку температура возрастает ( Фазовые переходы первого рода —при которых скачком изменяются первые производные термодинамических потенциалов по параметрам системы (температуре или давлению). Переходы первого рода реализуются как при переходе системы из одного агрегатного состояния в другое, так и в пределах одного агрегатного состояния.
Фазовые переходы второго рода — фазовые переходы, при которых первые производные
|
1. Траектория- это линия, описываемая движущимся телом относительно выбранной
системы отсчета. В зависимости от формы траектории движение подразделяют на прямолинейное и криволинейное.
2. Путь - длина траектории.
3. Перемещение - вектор, соединяющий начальную и конечную точки траектории.
4. Скорость 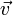 — векторная физическая величина, характеризующая быстроту
перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта.
5. Ускорение — векторная физическая величина, характеризующая быстроту
перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта.
5. Ускорение 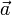 — производная скорости по времени, векторная величина, показывающая,
насколько изменяется вектор скорости точки (тела) при её движении за единицу времени.
Билет 3
1. Угол поворота - физическая величина, характеризующая поворот тела, или поворот
луча, исходящего из центра вращения тела, относительно другого луча, считающегося неподвижным.
2. Угловая скорость—векторная величина, равная первой производной угла поворота тела
по времени: — производная скорости по времени, векторная величина, показывающая,
насколько изменяется вектор скорости точки (тела) при её движении за единицу времени.
Билет 3
1. Угол поворота - физическая величина, характеризующая поворот тела, или поворот
луча, исходящего из центра вращения тела, относительно другого луча, считающегося неподвижным.
2. Угловая скорость—векторная величина, равная первой производной угла поворота тела
по времени: 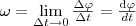 3. Угловое ускорение - векторная величина, равная первой производной угловой скорости по времени:
3. Угловое ускорение - векторная величина, равная первой производной угловой скорости по времени: 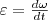 4. Основное уравнение динамики вращательного движения материальной точки – угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции. М = E*J или E = M/J
5. Центростремительное ускорение — компонента ускорения точки, характеризующая изменение направления вектора скорости для траектории с кривизной.
6. Полное ускорение точки складывается из касательного и нормального ускорений по правилу сложения векторов. Оно всегда будет направлено в сторону вогнутости траектории, поскольку в эту сторону направлено и нормальное ускорение.
7. Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости. Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи. При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь:
4. Основное уравнение динамики вращательного движения материальной точки – угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции. М = E*J или E = M/J
5. Центростремительное ускорение — компонента ускорения точки, характеризующая изменение направления вектора скорости для траектории с кривизной.
6. Полное ускорение точки складывается из касательного и нормального ускорений по правилу сложения векторов. Оно всегда будет направлено в сторону вогнутости траектории, поскольку в эту сторону направлено и нормальное ускорение.
7. Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости. Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи. При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь: 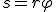 За малое время Δ t точка проходит расстояние
За малое время Δ t точка проходит расстояние 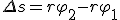 , где φ 2 и φ 1 — углы поворота в конце и в начале интервала Δ t. Разделив последнее равенство на Δ t и учитывая, что , где φ 2 и φ 1 — углы поворота в конце и в начале интервала Δ t. Разделив последнее равенство на Δ t и учитывая, что 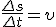 и и 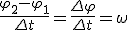 , получим , получим 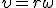 Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δ t есть
Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δ t есть 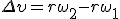 , где ω 2 и ω 1 — угловые скорости в конце и в начале промежутка Δ t. Разделим последнее равенство на Δ t и учтем, что , где ω 2 и ω 1 — угловые скорости в конце и в начале промежутка Δ t. Разделим последнее равенство на Δ t и учтем, что 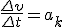 и и 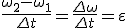 , тогда касательное ускорение , тогда касательное ускорение 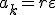 Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.
Билет 5
1. Сила тяжести - сила, с которой Земля притягивает к себе тело. Fтяж. Она всегда направлена
вертикально вниз. Сила тяжести прямо пропорциональна массе этого тела.
2. Сила упругости — сила, возникающая при деформации тела и противодействующая этой
деформации. В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности. Вектор силы противоположен направлению деформации тела (смещению его молекул).
3. Трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух
тел. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел. Четыре вида взаимодействий:
1)Электромагнитные взаимодействия тип фундаментальных взаимодействий, характеризуется участием электромагнитного поля в процессах взаимодействия. Электромагнитное поле либо излучается или поглощается при взаимодействии, либо переносит взаимодействие между телами. Так, притяжение между двумя неподвижными телами, обладающими разноимёнными электрическими зарядами, осуществляется посредством электрического поля, создаваемого этими зарядами; сила притяжения пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (закон Кулона).2)Сильное ядерное взаимодействие —В сильном взаимодействии участвуют кварки и галеоны и составленные из них частицы, называемые адронами. Оно действует в масштабах порядка размера атомного ядра и менее, отвечая за связь между кварками в адронах и за притяжение между нуклонами в ядрах. Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.
Билет 5
1. Сила тяжести - сила, с которой Земля притягивает к себе тело. Fтяж. Она всегда направлена
вертикально вниз. Сила тяжести прямо пропорциональна массе этого тела.
2. Сила упругости — сила, возникающая при деформации тела и противодействующая этой
деформации. В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности. Вектор силы противоположен направлению деформации тела (смещению его молекул).
3. Трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух
тел. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел. Четыре вида взаимодействий:
1)Электромагнитные взаимодействия тип фундаментальных взаимодействий, характеризуется участием электромагнитного поля в процессах взаимодействия. Электромагнитное поле либо излучается или поглощается при взаимодействии, либо переносит взаимодействие между телами. Так, притяжение между двумя неподвижными телами, обладающими разноимёнными электрическими зарядами, осуществляется посредством электрического поля, создаваемого этими зарядами; сила притяжения пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (закон Кулона).2)Сильное ядерное взаимодействие —В сильном взаимодействии участвуют кварки и галеоны и составленные из них частицы, называемые адронами. Оно действует в масштабах порядка размера атомного ядра и менее, отвечая за связь между кварками в адронах и за притяжение между нуклонами в ядрах.
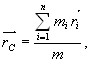 3)Слабое взаимодействие—Оно ответственно, в частности, за бета-распад ядра. Слабое взаимодействие является короткодействующим — оно проявляется на расстояниях, значительно меньших размера атомного ядра (характерный радиус взаимодействия 10− 18 м). Стандартная модель физики элементарных частиц описывает электромагнитное взаимодействие и слабое взаимодействие как разные проявления единого электро слабого взаимодействия.4)Гравитационное взаимодействие —гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, согласно которому сила гравитационного притяжения между двумя телами массы 3)Слабое взаимодействие—Оно ответственно, в частности, за бета-распад ядра. Слабое взаимодействие является короткодействующим — оно проявляется на расстояниях, значительно меньших размера атомного ядра (характерный радиус взаимодействия 10− 18 м). Стандартная модель физики элементарных частиц описывает электромагнитное взаимодействие и слабое взаимодействие как разные проявления единого электро слабого взаимодействия.4)Гравитационное взаимодействие —гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, согласно которому сила гравитационного притяжения между двумя телами массы 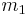 и и 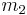 , разделённых расстоянием , разделённых расстоянием 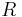 есть есть 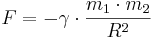 Здесь Здесь 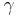 — гравитационная постоянная, равная — гравитационная постоянная, равная 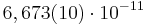 м3/(кг с2). Знак минус означает, что сила, действующая на пробное тело, всегда направлена по радиус-вектору от пробного тела к источнику гравитационного поля, т. е. гравитационное взаимодействие приводит всегда к притяжению тел. В механике Галилея—Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен где м3/(кг с2). Знак минус означает, что сила, действующая на пробное тело, всегда направлена по радиус-вектору от пробного тела к источнику гравитационного поля, т. е. гравитационное взаимодействие приводит всегда к притяжению тел. В механике Галилея—Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен где 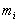 и и 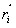 - соответственно масса и радиус-вектор - соответственно масса и радиус-вектор 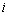 -й материальной точки; -й материальной точки; 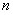 - число материальных точек в системе; - число материальных точек в системе; 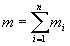 - масса системы.
Билет 7.
1. Консервативная сила - сила, работа которой не зависит от пути перехода тела или
системы из начального положения в конечное. К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы. Характерное свойство такой силы – работа на замкнутой траектории равна нулю: - масса системы.
Билет 7.
1. Консервативная сила - сила, работа которой не зависит от пути перехода тела или
системы из начального положения в конечное. К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы. Характерное свойство такой силы – работа на замкнутой траектории равна нулю:
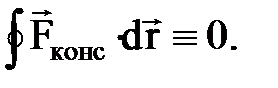 2. Диссипативная(неконсервативная) сила— сила, работа которой зависит от пути
перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
3. Потенциальное поле.-- взаимодействие тел, которая осуществляется посредством
силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Консервативное поле- поле действующее на потенциальное поле.
4. Потенциальная энергия
2. Диссипативная(неконсервативная) сила— сила, работа которой зависит от пути
перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
3. Потенциальное поле.-- взаимодействие тел, которая осуществляется посредством
силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Консервативное поле- поле действующее на потенциальное поле.
4. Потенциальная энергия 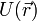 — скалярная физическая величина, характеризующая
способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым, и описывающая взаимодействие элементов системы.
5. Работа. Работа, которую может совершить растянутая пружина при перемещении
ее конца, зависит только от начального и конечного растяжений пружины.
Пусть, например, растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. При нахождении работы мы должны учитывать, что сила, с которой действует пружина, не остается постоянной при изменении растяжения. Мы видели (§ 37), что сила упругости пружины пропорциональна ее растяжению. Если первоначальное растяжение пружины, считая от ее нерастянутого состояния, равнялось l, то первоначальное значение силы упругости составляло F=kl, где k — коэффициент пропорциональности, который называют коэффициентом упругости пружины. По мере сокращения пружины эта сила равномерно убывает от значения kl до нуля.Значит, среднее значение силы равно Fср=kl. Можно показать, что для вычисления работы А изменяющейся силы упругости нужно это среднее значение силы умножить на перемещение точки приложения силы:
A=1/2 kl•l=1/2kl2.
Таким образом, потенциальная энергия упругости Еп равна — скалярная физическая величина, характеризующая
способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым, и описывающая взаимодействие элементов системы.
5. Работа. Работа, которую может совершить растянутая пружина при перемещении
ее конца, зависит только от начального и конечного растяжений пружины.
Пусть, например, растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. При нахождении работы мы должны учитывать, что сила, с которой действует пружина, не остается постоянной при изменении растяжения. Мы видели (§ 37), что сила упругости пружины пропорциональна ее растяжению. Если первоначальное растяжение пружины, считая от ее нерастянутого состояния, равнялось l, то первоначальное значение силы упругости составляло F=kl, где k — коэффициент пропорциональности, который называют коэффициентом упругости пружины. По мере сокращения пружины эта сила равномерно убывает от значения kl до нуля.Значит, среднее значение силы равно Fср=kl. Можно показать, что для вычисления работы А изменяющейся силы упругости нужно это среднее значение силы умножить на перемещение точки приложения силы:
A=1/2 kl•l=1/2kl2.
Таким образом, потенциальная энергия упругости Еп равна
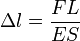 Билет 9
1. Полная механическая энергия E- сумма потенциальной и кинетической энергии
E = Eп + Eк.
Закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которым и действуют только консервативные силы, остается постоянной. При отсутствии диссипативных сил (например, силы трения) механическая энергия не возникает из ничего и не может исчезнуть никуда. Классический пример является пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза )переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия ) и обратно. В случае математического маятника аналогично ведет себя потенциальная энергия груза в поле силы тяжести. Вывод из уравнений Ньютона (учитываются все потенциальные силы в консервативной системе, действующие на тело).
Билет 9
1. Полная механическая энергия E- сумма потенциальной и кинетической энергии
E = Eп + Eк.
Закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которым и действуют только консервативные силы, остается постоянной. При отсутствии диссипативных сил (например, силы трения) механическая энергия не возникает из ничего и не может исчезнуть никуда. Классический пример является пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза )переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия ) и обратно. В случае математического маятника аналогично ведет себя потенциальная энергия груза в поле силы тяжести. Вывод из уравнений Ньютона (учитываются все потенциальные силы в консервативной системе, действующие на тело). 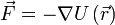 ,
где ,
где 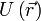 — потенциальная энергия материальной точки ( — потенциальная энергия материальной точки ( 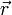 — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид 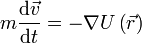 , где , где 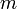 — масса частицы, — масса частицы, 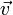 — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что 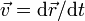 , можно получить , можно получить 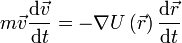 Путём элементарных операций это выражение может быть приведено к следующему виду Путём элементарных операций это выражение может быть приведено к следующему виду 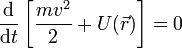 Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной. Этот вывод может быть легко обобщён на систему материальных точек[2].
2. Работа-физическая величина, численно равная произведению силы на перемещение в в направлении действия этой силы и ей же вызванное A=F*s. Если перемещение по направлению не совпадает с направлением действия силы, то появляется косинус угла.
Билет 11. Момент силы. Основное уравнение динамики вращающегося твердого тела. Условия равновесия твердого тела.
1. Момент силы— векторная физическая величина, равная произведению радиус-вектора,
проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
M=Ie; основной закон динамики твердого тела произведение момента инерции твердого тела относительно оси вращения на его угловое ускорение равно суммарному моменту внешних сил относительно той же оси. Этот закон-аналог второго закона Ньютона. При этом аналог линейного ускорения служит угловое ускорение, аналогом сил- их моменты, а аналогом массы-момент инерции.
Равенство действующих на тело сил.Статикой называется раздел механики, изучающий условия равновесия тел.Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной. Этот вывод может быть легко обобщён на систему материальных точек[2].
2. Работа-физическая величина, численно равная произведению силы на перемещение в в направлении действия этой силы и ей же вызванное A=F*s. Если перемещение по направлению не совпадает с направлением действия силы, то появляется косинус угла.
Билет 11. Момент силы. Основное уравнение динамики вращающегося твердого тела. Условия равновесия твердого тела.
1. Момент силы— векторная физическая величина, равная произведению радиус-вектора,
проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
M=Ie; основной закон динамики твердого тела произведение момента инерции твердого тела относительно оси вращения на его угловое ускорение равно суммарному моменту внешних сил относительно той же оси. Этот закон-аналог второго закона Ньютона. При этом аналог линейного ускорения служит угловое ускорение, аналогом сил- их моменты, а аналогом массы-момент инерции.
Равенство действующих на тело сил.Статикой называется раздел механики, изучающий условия равновесия тел.Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. 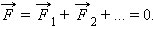 Билет 13.
Скатывание с горки двух цилиндров, пустого и сплошного.
У полого тонкостенного цилиндра радиуса R и массы m, на оси цилиндра момент инерции будет I = m*R^2 У сплошного цилиндра радиуса R и массы m, на оси момент инерции будет I = m*R^2/2 - то есть в два раза меньше В свою очередь, полная кин энергия тел есть
Билет 13.
Скатывание с горки двух цилиндров, пустого и сплошного.
У полого тонкостенного цилиндра радиуса R и массы m, на оси цилиндра момент инерции будет I = m*R^2 У сплошного цилиндра радиуса R и массы m, на оси момент инерции будет I = m*R^2/2 - то есть в два раза меньше В свою очередь, полная кин энергия тел есть 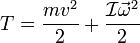 и равна m*g*h учтем также, что w = v/R Другими словами: mgh = v^2*(I/2R + m/2) v^2 = mgh/(I/2R + m/2) то есть, чем больше момент инерции I, тем меньше скорость тела (тонкостенного цилиндра).
Билет 15
Стационарное течение идеальной жидкости. Уравнение Бернули.
Течение жидкости называют стационарным (установившимся), если форма и расположение линий тока, а также скорости в каждой точке жидкости, со временем не изменяются.
Рассмотрим несжимаемую жидкость: , s1v1 = s2v2. Это соотношение справедливо для любых сечений трубки, следовательно,
sv = const физический смысл произведения sv -объем жидкости, проходящей через сечение s за 1 с.
Идеальная жидкость - это жидкость, в которой отсутствуют силы внутреннего трения .
Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения. В момент времени t жидкость заполняла участок ограниченный S1 и S2,
а в момент времени, она занимает объём и. В силу неразрывности струи заштрихованные объёмы будут иметь одинаковую величину.
По закону сохранения энергии: ;
v12/2 + gh1 + p1 = v22/2 + gh2 + p2; или rv2/2 + rgh + p = const -ур-ние Бернулли.
Уравнение Бернулли есть выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости.
Величину р называют статистическим давлением, величину v2/2 называютдинамическим давлением, а величина gh является гидростатическим давлением.
Для горизонтальной трубки тока уравнение Бернулли имеет вид rv2/2 + p = const, где величина rv2/2 + p называется полным давлением. Из последнего уравнения и уравнения неразрывности следует, что при течение жидкости по горизонтальной трубке, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах.
Если жидкость неподвижна v=0, то p1 и p2=const и полное давление определяется гидростатическим и статическим давлением.
Билет 17.
Поверхностная энергия и натяжение. Капиллярные явления.
Поверхностная энергия. Молекулы поверхностного слоя жидкости обладают дополнительной потенциальной энергией по сравнению с молекулами внутри жидкости. Эту энергию называют поверхностной энергией. Величина поверхностной энергии тем больше, чем больше площадь свободной поверхности и равна m*g*h учтем также, что w = v/R Другими словами: mgh = v^2*(I/2R + m/2) v^2 = mgh/(I/2R + m/2) то есть, чем больше момент инерции I, тем меньше скорость тела (тонкостенного цилиндра).
Билет 15
Стационарное течение идеальной жидкости. Уравнение Бернули.
Течение жидкости называют стационарным (установившимся), если форма и расположение линий тока, а также скорости в каждой точке жидкости, со временем не изменяются.
Рассмотрим несжимаемую жидкость: , s1v1 = s2v2. Это соотношение справедливо для любых сечений трубки, следовательно,
sv = const физический смысл произведения sv -объем жидкости, проходящей через сечение s за 1 с.
Идеальная жидкость - это жидкость, в которой отсутствуют силы внутреннего трения .
Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения. В момент времени t жидкость заполняла участок ограниченный S1 и S2,
а в момент времени, она занимает объём и. В силу неразрывности струи заштрихованные объёмы будут иметь одинаковую величину.
По закону сохранения энергии: ;
v12/2 + gh1 + p1 = v22/2 + gh2 + p2; или rv2/2 + rgh + p = const -ур-ние Бернулли.
Уравнение Бернулли есть выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости.
Величину р называют статистическим давлением, величину v2/2 называютдинамическим давлением, а величина gh является гидростатическим давлением.
Для горизонтальной трубки тока уравнение Бернулли имеет вид rv2/2 + p = const, где величина rv2/2 + p называется полным давлением. Из последнего уравнения и уравнения неразрывности следует, что при течение жидкости по горизонтальной трубке, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах.
Если жидкость неподвижна v=0, то p1 и p2=const и полное давление определяется гидростатическим и статическим давлением.
Билет 17.
Поверхностная энергия и натяжение. Капиллярные явления.
Поверхностная энергия. Молекулы поверхностного слоя жидкости обладают дополнительной потенциальной энергией по сравнению с молекулами внутри жидкости. Эту энергию называют поверхностной энергией. Величина поверхностной энергии тем больше, чем больше площадь свободной поверхности
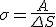 .
Единицей коэффициента поверхностного натяжения в СИ является джоуль на квадратный метр (Дж/м2).
Поверхностное натяжение
Равнодействующая сил, действующих на все молекулы, находящиеся на границе свободной поверхности, и есть сила поверхностного натяжения. В целом она действует так, что стремится сократить поверхность жидкости. .
Единицей коэффициента поверхностного натяжения в СИ является джоуль на квадратный метр (Дж/м2).
Поверхностное натяжение
Равнодействующая сил, действующих на все молекулы, находящиеся на границе свободной поверхности, и есть сила поверхностного натяжения. В целом она действует так, что стремится сократить поверхность жидкости.
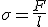 .
Согласно этой формуле единицей коэффициента поверхностного натяжения в СИ является ньютон на метр (Н/м).
Коэффициент поверхностного натяжения σ численно равен силе поверхностного натяжения, действующей на единицу длины границы свободной поверхности жидкости. Коэффициент поверхностного натяжения зависит от природы жидкости, от температуры и от наличия примесей. При увеличении температуры он уменьшается.
Капиллярные явления, физические явления, обусловленные действием поверхностного натяжения на границе раздела несмешивающихся сред. К К. я. относят обычно явления в жидких средах, вызванные искривлением их поверхности, граничащей с др. жидкостью, газом или собственным паром. Искривление поверхности ведёт к появлению в жидкости дополнительного капиллярного давления Dp, величина которого связана со средней кривизной r поверхности уравнением Лапласа: Dp = p1 — p2. = 2s12/r, где (s12 — поверхностное натяжение на границе двух сред; p1 и p2 — давления в жидкости 1 и контактирующей с ней среде.
Билет 19.
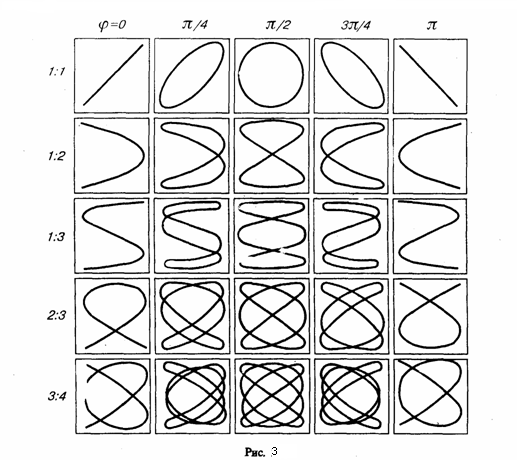
Сложение гармонических колебаний одного направления, взаимноперпендекулярных. Фигуры Листажу.
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты .
Согласно этой формуле единицей коэффициента поверхностного натяжения в СИ является ньютон на метр (Н/м).
Коэффициент поверхностного натяжения σ численно равен силе поверхностного натяжения, действующей на единицу длины границы свободной поверхности жидкости. Коэффициент поверхностного натяжения зависит от природы жидкости, от температуры и от наличия примесей. При увеличении температуры он уменьшается.
Капиллярные явления, физические явления, обусловленные действием поверхностного натяжения на границе раздела несмешивающихся сред. К К. я. относят обычно явления в жидких средах, вызванные искривлением их поверхности, граничащей с др. жидкостью, газом или собственным паром. Искривление поверхности ведёт к появлению в жидкости дополнительного капиллярного давления Dp, величина которого связана со средней кривизной r поверхности уравнением Лапласа: Dp = p1 — p2. = 2s12/r, где (s12 — поверхностное натяжение на границе двух сред; p1 и p2 — давления в жидкости 1 и контактирующей с ней среде.
Билет 19.
Сложение гармонических колебаний одного направления, взаимноперпендекулярных. Фигуры Листажу.
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты
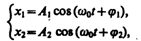 воспользовавшись методом вращающегося вектора амплитуды. Построим векторные диаграммы этих колебаний (рис. 203). Tax как векторы A1 и А2 вращаются с одинаковой угловой скоростью w0, то разность фаз (j2—j1)между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет
воспользовавшись методом вращающегося вектора амплитуды. Построим векторные диаграммы этих колебаний (рис. 203). Tax как векторы A1 и А2 вращаются с одинаковой угловой скоростью w0, то разность фаз (j2—j1)между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет
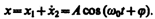 Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде
Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде 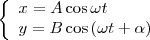 (1) где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t.
Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Листажу. Отношение частот складываемых колебаний равно отношению числа пересечений фигур Листажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. (1) где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t.
Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Листажу. Отношение частот складываемых колебаний равно отношению числа пересечений фигур Листажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний.
 3.Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника
3.Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника 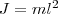 (8) где l — длина маятника. Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника (8) где l — длина маятника. Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника 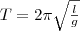 Билет 22.
Гармонический осциллятор. Вынужденные колебания, дифференциальное уравнение вынужденных колебаний и его решение. Резонанс.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Второй закон Ньютона для такого осциллятора запишется в виде:
Билет 22.
Гармонический осциллятор. Вынужденные колебания, дифференциальное уравнение вынужденных колебаний и его решение. Резонанс.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Второй закон Ньютона для такого осциллятора запишется в виде: 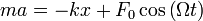 . Если ввести обозначения: . Если ввести обозначения: 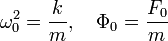 и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение: и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:
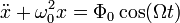 Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:
Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:
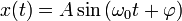 ,
где ,
где 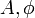 — произвольные постоянные, которые определяются из начальных условий.
Найдём частное решение. Для этого подставим в уравнение решение вида: — произвольные постоянные, которые определяются из начальных условий.
Найдём частное решение. Для этого подставим в уравнение решение вида: 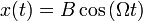 и получим значение для константы: и получим значение для константы:
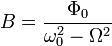 Тогда окончательное решение запишется в виде:
Тогда окончательное решение запишется в виде:
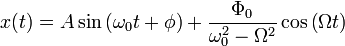 Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания
Резонанс
Из решения видно, что при частоте вынуждающей силы, равной частоте свободных колебаний, оно не пригодно — возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курса математического анализа известно, что решение в этом случае надо искать в виде:
Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания
Резонанс
Из решения видно, что при частоте вынуждающей силы, равной частоте свободных колебаний, оно не пригодно — возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курса математического анализа известно, что решение в этом случае надо искать в виде: 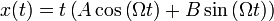 . Подставим этот анзац в дифференциальное уравнение и получим, что: . Подставим этот анзац в дифференциальное уравнение и получим, что:
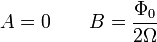 Таким образом, колебания в резонансе будут описываться следующим соотношением: Таким образом, колебания в резонансе будут описываться следующим соотношением:
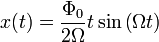 Билет 24.
Стоячие волны. Амплитуда стоячей волны. Узлы и пучности. Длина стоячей волны.
При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит.
Для волны, бегущей по оси x:
Билет 24.
Стоячие волны. Амплитуда стоячей волны. Узлы и пучности. Длина стоячей волны.
При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит.
Для волны, бегущей по оси x:
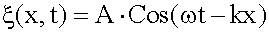 Для волны, бегущей против оси x: Для волны, бегущей против оси x: 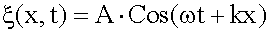 Амплитуда стоячей волны - это модуль выражения, стоящего перед множителем Cosω t, т.е.
Амплитуда стоячей волны - это модуль выражения, стоящего перед множителем Cosω t, т.е.
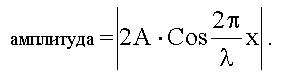 Узлы и пучности. Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:
Узлы и пучности. Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов: 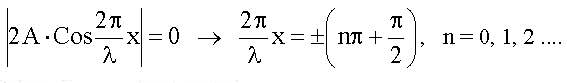 Следовательно, координаты узлов: Следовательно, координаты узлов:
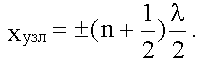 Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны.
Для пучностей:
Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны.
Для пучностей: 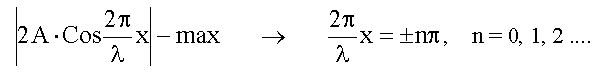 Координаты пучностей:
Координаты пучностей: 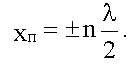 Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно
Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно 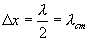 где λ - длина бегущей волны.
Билет 27.
Применение первого начала к изопроцессам: адиабатический процесс.
Адиабатическимназывается процесс, при котором отсутствует теплообмен (dQ=0).
Из первого начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что
dA=-dU,
Продифференцировав уравнение состояния для идеального газа pV=(m/M)RT, получим
Исключим температуру Т:
Разделив переменные и учитывая, что Ср/Сv =g , найдем dp/p=-gdV/V.
Интегрируя это уравнение в пределах от р1до р2и соответственно от V1до V2, а затем потенцируя, придем к выражению
p2/pl=(V1/V2)g. или p1vg1 = p2vg2.
Так как состояния 1 и 2 выбраны произвольно, то можно записать
рVg=const.
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
Изотермический процесс (T=const), изотермический процесс описывается законом Бойля—Мариотта:
работу изотермического расширения газа: где λ - длина бегущей волны.
Билет 27.
Применение первого начала к изопроцессам: адиабатический процесс.
Адиабатическимназывается процесс, при котором отсутствует теплообмен (dQ=0).
Из первого начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что
dA=-dU,
Продифференцировав уравнение состояния для идеального газа pV=(m/M)RT, получим
Исключим температуру Т:
Разделив переменные и учитывая, что Ср/Сv =g , найдем dp/p=-gdV/V.
Интегрируя это уравнение в пределах от р1до р2и соответственно от V1до V2, а затем потенцируя, придем к выражению
p2/pl=(V1/V2)g. или p1vg1 = p2vg2.
Так как состояния 1 и 2 выбраны произвольно, то можно записать
рVg=const.
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
Изотермический процесс (T=const), изотермический процесс описывается законом Бойля—Мариотта:
работу изотермического расширения газа:
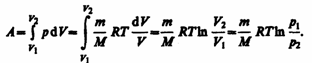 Так как при Т=const внутренняя энергия идеального газа не изменяется: Так как при Т=const внутренняя энергия идеального газа не изменяется: 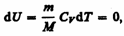 то из первого начала термодинамики (dQ=dU+dA) следует, что для изотермического процесса
то из первого начала термодинамики (dQ=dU+dA) следует, что для изотермического процесса
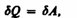 т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил: 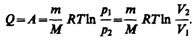 Следовательно, для того чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
Билет 29.Тепловые двигатели и холодные машины. Паровой двигатель, двигатель внутреннего сгорания, турбина, холодильник.
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества. Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно Q = Q1 + Q2 = Q1 – |Q2|. При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (Δ U = 0). Согласно первому закону термодинамики, При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (Δ U = 0). Согласно первому закону термодинамики, Δ U = Q – A = 0. коэффициентом полезного действия η тепловой машины:
Следовательно, для того чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
Билет 29.Тепловые двигатели и холодные машины. Паровой двигатель, двигатель внутреннего сгорания, турбина, холодильник.
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества. Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно Q = Q1 + Q2 = Q1 – |Q2|. При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (Δ U = 0). Согласно первому закону термодинамики, При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (Δ U = 0). Согласно первому закону термодинамики, Δ U = Q – A = 0. коэффициентом полезного действия η тепловой машины: 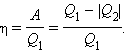
Паровая машина — тепловой двигатель внешнего сгорания, преобразующий энергию пара в механическую работу возвратно-поступательного движения поршня, а затем во вращательное движение вала. В более широком смысле паровая машина — любой двигатель внешнего сгорания, который преобразовывает энергию пара в механическую работу. Для привода паровой машины необходим паровой котёл. Расширяющийся пар давит на поршень или на лопатки паровой турбины, движение которых передаётся другим механическим частям. Одно из преимуществ двигателей внешнего сгорания в том, что из-за отделения котла от паровой машины можно использовать практически любой вид топлива — от кизяка до урана. Двигатель внутреннего сгорания (сокращённо ДВС ) — это тип двигателя, тепловой машины, в которой химическая энергия топлива (обычно применяется жидкое или газообразное углеводородное топливо), сгорающего в рабочей зоне, преобразуется в механическую работу. В отличие от паровых машин здесь топливо сжигается для нагревания газа, а не для превращения жидкости в пар. Правда, наряду с нагреванием воздуха происходит и частичное изменение его состава: вместо молекул кислорода появляется несколько большее количество молекул углекислого газа и водяного пара Газовая турбина — это двигатель непрерывного действия, в лопаточном аппарате которого энергия сжатого или нагретого газа преобразуется в механическую работу на валу. Горение топлива может происходить как вне турбины, так и в самой турбине. Основными элементами конструкции являются ротор (рабочие лопатки, закреплённые на дисках) и статор, выполненный в виде выравнивающего аппарата (направляющие лопатки, закреплённые в корпусе). Газ под высоким давлением поступает через сопловой аппарат турбины в область низкого давления, при этом расширяясь и ускоряясь. Далее, поток газа попадает на рабочие лопатки турбины, отдавая им часть своей кинетической энергии и сообщая лопаткам крутящий момент. Рабочие лопатки передают крутящий момент через диски турбины на вал
Билет 31. Популярное:
|
Последнее изменение этой страницы: 2016-07-12; Просмотров: 815; Нарушение авторского права страницы