
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
в управлении агрегатным станком ⇐ ПредыдущаяСтр 6 из 6
Если в помеченной таким образом таблице окажется, что в каком-либо интервале с отметкой на линии Y отсутствует отметка на линии X, то, значит, в данном случае смена управляющих сигналов на исполнительные органы произошла вследствие поступления сигналов от времязадающего устройства (таймера). Во всех остальных случаях признаком наступления нового интервала служит новое сочетание сигналов X, и τ k при этом должна принять единичное значение. Для того чтобы в результате опроса всех входов функция τ k; принимала единичное значение при переходе к следующему интервалу, эта функция строится как конъюнкция всех аргументов Xi. При этом те аргументы Xi, которые в соответствии с циклограммой включений на границе рассматриваемых интервалов сохраняют единичное значение либо изменяются с 1 на 0, входят в такую конъюнкцию без отрицания. Также без отрицания входят в конъюнкцию аргументы, которые изменяются на границе данных интервалов с 0 на 1. И лишь аргументы, сохраняющие при переходе к новому интервалу ранее имевшееся нулевое значение, входят в эту конъюнкцию с отрицанием. Это может быть записано в виде соотношения
где аi = 1, если по циклограмме включений Хi (k) = 1 и Xi(k + 1) = 1, либо Хi(k) = 1 и Xi(k + 1) = 0, либо Xi (k) = 0 и Xi (k + 1) = 1, и α i = 0, если по циклограмме включений
Возвращаясь к нашему примеру, по диаграмме изменений состояний векторов входов и выходов (см. рис. 36) замечаем, что в моменты k=3и k=11происходит изменение состояния выходов Y без изменения состояния входов X. Иными словами, включение движения питателя и гидроцилиндра зажима детали должно происходить без дополнительных внешних сигналов через определенное время после начала 'рабочей подачи силовых головок. Точно так же обратный ход питателя должен начаться через определенное время после быстрого отвода силовых головок в исходное положение. В эти моменты сигналы на включение исполнительных органов Y6, Y7, а также U7, должны, выдаваться по командам от внутренней организующей программы, например от супервизора реального времени. Во все остальные моменты соответствующие выходы включаются от блока генерации функции τ k, когда логические уcловия перехода к новому интервалу принимают значения истинности. В рассматриваемом случае, руководствуясь сформулированными выше правилами, запишем выражения для логических условий перехода к новому интервалу времени (элементу цикла) в следующем виде:
Эти же соотношения используются для включения программируемых временных задержек или выдачи уставок на супервизор реального времени. Возможна и более простая формальная запись таких соотношений в виде таблицы условий. Столбцы такой таблицы нумеруются индексами переменных X, а строки — индексами функций т. В клетках таблицы можно ставить, например, минус, если в выражение данной функции данный аргумент входит с отрицанием, и оставлять их пустыми в противоположном случае. Функционирование ЭВМ для реализации подобных логических соотношений организуется следующим образом. По указаниям организующей программы ЭВМ периодически, но не реже чем один раз за 0, 01 сек.(допустимое время задержки реакции управляющей ЭВМ на поступление конца элемента цикла) опрашивает все входные сигналы X и проверяет их совпадение с характерным для данного элемента цикла сочетанием условий (например,
Такая организация управления цикловыми процессами во времени оказывается приемлемой при сравнительно небольшом числе опрашиваемых входов. Если же число входов и выходов достигает десятков и более, что характерно для управления сложными станками и автоматическими линиями, необходимо использовать более экономные принципы организации управления. Сущность предлагаемого для таких случаев алгоритма заключается в том, что операции управления разбиваются на независимые группы, соответствующие отдельным узлам, затем выполняются программы, синхронизирующие в пределах одного станка работу программ, реализующих управление отдельными узлами, а в случае необходимости в работу включаются программы, синхронизирующие программы синхронизации в пределах линии.
Дегтярев Ю.И. Методы оптимизации 10.4. Планирование многоэтапных работ. Пошаговый процесс упорядочения. Рассматриваемая здесь задача представляет собой обобщение известной задачи Джонсона на случай произвольного M> 2. Ее решение в рамках общего алгоритма системного планирования (см. п. 9.5) позволяет не только улучшать промежуточные значения Т0, но и указывать те l-системы, для которых нет необходимости составлять точное расписание. Дана система, объединяющая M одноканальных участков, каждый из которых реализует вполне определенный этап технологического процесса. Имеются N работ, выполняемых в некоторой последовательности, и известны нормы времени τ vk (v — номер работы по порядку следования, k — номер участка или этапа). Введены ограничения: а) очередность работ сохраняется на всех участках неизменной (допустимость такого предположения обусловлена здесь тем, что оно упрощает исследования и затем постепенно исключается в ходе преобразования общесистемного плана); б) момент начала k-го этапа v -й работы не может наступить раньше момента окончания ее (k—1)-го этапа; в) для отдельных работ установлены плановые сроки окончания, которые необходимо выдержать; г) возможна частичная упорядоченность работ (некоторые из них не должны проводиться раньше каких-то других).
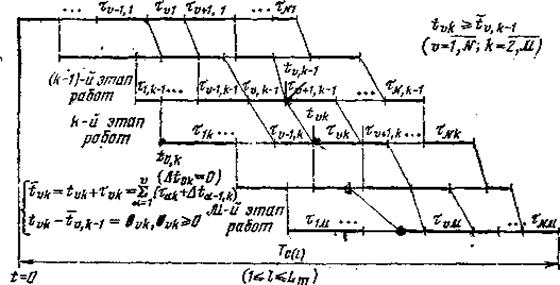 В этих условиях требуется найти последовательность работ, наилучшую в смысле минимума полного времени (Тc(l)), затрачиваемого на их выполнение (рис. 10.8). В этих условиях требуется найти последовательность работ, наилучшую в смысле минимума полного времени (Тc(l)), затрачиваемого на их выполнение (рис. 10.8).
Перечисленные ограничения не противоречат тому, что обсуждалось в § 8.5, и даны для конкретизации общих замечаний применительно к частной задаче. Введем единый отсчет времени (t=0); пусть t0k— момент возможного начала k-ro этапа, а ∆ tv-1, k— задержка начала k-ro этапа v-й работы относительно момента окончания того же этапа (v—1) работы. Очевидно, ∆ tv-1, k ≥ 0, и условие б) может быть выражено как
или
Последнее равенство показывает, что v-я(по порядку) работа будет выполнена за время Объединив номера v, для которых существуют плановые сроки, в множество Sn, получаем формальное выражение условия в):
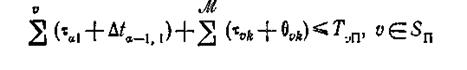
или
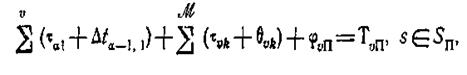
где φ vП — вспомогательные неотрицательные переменные. Условия а) и г) связывают порядковые номера, которые получают работы, проводимые в оптимальной последовательности, поэтому формализация этих условий априори ничего не дает.
Система уравнений (10.5) может быть представлена в виде
или (после попарного вычитания строк) Заметим, что всегда можно положить Δ t0k(k=1, M), равными нулю (или, что то же, включить их условно в τ 1k). Кроме того, работы подготовительные, регламентные и т. п. могут быть учтены наравне со всеми другими работами в общих соотношениях вида (10.5) — (10.7).
Зафиксировав произвольным образом все τ vk, рассмотрим эту задачу как обычную задачу линейного программирования. Из выражения Tc(l) следует, что всякое допустимое базисное решение системы (10.8), содержащее в числе свободных переменные Δ tv-1, 1(v=2, N), Θ Nk (k=2, M) будет оптимальным для сформулированной задачи. Однако подобные решения могут встретиться далеко не всегда, поэтому необходимы дополнительные исследования. Обратимся к теореме (22): оптимальным является такое допустимое базисное решение (10.8), которое содержит в числе свободных все Δ tv-1, 1 и одновременно удовлетворяет требованиям Θ vkΔ tv-1, k=0, (v=2, N, k=2, M) (переменная Θ vk может войти в базис только тогда, когда Δ tv-1, k является свободной и наоборот). Доказательство этой теоремы основано на последовательном отделении заведомо свободных переменных Θ vk (см. § 9.1). Чтобы найти оптимальные решения в каждом конкретном случае, достаточно использовать простое правило: если в очередной строке (10.8) сумма Δ tv-1, k-1 — Θ v-1, k + ω vk неотрицательна, то в базис вводится Δ tv-1, k, а Θ vk считается свободной (равной нулю). Если же Δ tv-1, k-1 — Θ v-1, k + ω vk < 0, базисной переменной становится Θ vk, а Δ tv-1, k обращается в нуль. Сформированное решение должно удовлетворять требованиям φ vП ≥ 0 (vЄ SП), иначе оно окажется недопустимым. В этих условиях можно говорить об оптимальной организации работ даже при фиксированном порядке их производства (не нарушающем ограничений а) — г)). Так, этапы работы, выполняемой первой, должны следовать друг за другом без задержек (Θ 1k=0, k=2, M); этапы любой промежуточной работы идут, вообще говоря, со сдвигами во времени один относительно другого. Исключение составляет случай, когда все
Полученные результаты неконструктивны (они отвечают предположению τ vk=const и не дают рекомендаций по выбору наилучшего плана проведения работ), однако появляется возможность отождествить произвольную перестановку столбцов матрицы ||τ kv|| с некоторым показателем, вычисляемым довольно просто, что должно облегчить применение здесь метода динамического программирования (или методов, сходных с ним по идее). Условия для этого следующие: — рассматривается N-шаговый процесс планирования; — содержанием очередного шага является размещение того или иного столбца на определенной позиции; — перед началом очередного шага возможны только N состояний процесса, причем параметр состояния скалярный (номер столбца). Рассмотрим теперь время Tc(l) как функцию только τ vk (v=1, N, k=1, M), имея в виду найденные решения. Оценка Ť c(i), получаемая при использовании рекомендаций приведенной выше теоремы и обозначаемая как Ť c(l), обладает рядом особенностей: в общем случае Ť c(l) представляет собой линейную комбинацию величин τ vk, т. е.
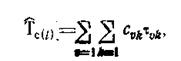
где cvk — целочисленные коэффициенты; каждое значение Ť c(l) отвечает заданному порядку работ, который в силу условия а) определяется порядком проведения их первого этапа (т. е. принятыми τ v-1, (v=1, N), следовательно, τ vk есть однозначно определенная функция τ v, 1, (v=1, N). Учитывая эти замечания, получаем Возможные наборы значений τ v1 образуются при перестановках N' элементов первой строки матрицы ║ τ kv║ , и множество всех таких перестановок объединяет N! элементов. Наиболее удобным для практической реализации представляется метод поиска оптимума Ť c(l) по переменным τ v1 основанный на идее непосредственного пошагового формирования искомой расстановки работ и сводящийся к анализу промежуточных состоянии и наилучших продолжений процесса планирования. Исходными данными здесь являются конкретизированные ограничения в), г) и матрица ║ τ kv║ с фиксированной произвольным образом нумерацией столбцов (исходная нумерация работ). Основные этапы решения задачи: вводится предположение о том, что (N — 1)-ю позицию занимает первая (по исходной нумерации) работа, и в рамках этого предположения исследуются варианты формирования двух последних позиций будущего плана («первая и вторая работы», «первая и третья работы», ..., «первая и N-я работы»); для каждого такого варианта определяются ω vk=τ v, k-1- τ v-1, k, Δ tv-1, k при v=N, k=2, M. Проверяется выполнение условий в), г) и оцениваются величины Ť c(l)=То + Рассмотренные операции повторяются для оставшихся предположений, связанных с размещением третьей, четвертой, ..., N-й работы на (N — 1) -й позиции. Таким образом, оказываются исследованными N(N — 1) вариантов, и становится возможным их сравнение с целью указать наилучшие из полученных Ť c(l). (все это удобно свести в первую таблицу результатов, содержащую перечни вариантов, допустимых по ограничениям а) — г) и упорядоченных по признаку ухудшения Ť c(l).). Вводится предположение о том, что (N — 2) -ю позицию занимает первая (по исходной нумерации) работа. В рамках этого предположения исследуются варианты формирования трех последних позиций будущего плана, причем (N — 1) -я и N -я позиции (т. е. продолжение процесса) выбираются здесь как единое целое на основе использования данных первой таблицы результатов. Определяются Θ vk, Δ tv-1, k(v=2, N-1; k=2, M), проверяются условия в), г) (по оптимистическим показателям) и оцениваются новые величины , М
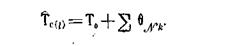
Все эти операции повторяются применительно к предположениям, связанным с размещением второй, третьей, ..., N-й работ на (N — 2) -и позиции, так что общее число анализируемых вариантов составляет по-прежнему N(N — 1). Все результаты, не нарушающие ограничений а) — г), сводятся во вторую таблицу. Вводится предположение о том, что (N — 3)-ю позицию занимает первая (по исходной нумерации) работа, и исследуются варианты формирования четырех последних позиций будущего плана. Набор работ, попадающих па (N — 2)-ю, (N — 1)-ю, N-ю позиции, дает вторая таблица результатов; проводятся стандартные проверки условий в), г), вычисляются Ť c(l)., и, наконец, составляется третья таблица результатов; переход к новым предположениям продолжается до тех пор, пока не будут составлены и оценены последовательности из N работ. Общее количество исследуемых вариантов в рассмотренной схеме не превысит N3 вместо N! при полном переборе (реальный выигрыш получается при N> 5).
Популярное:
|
Последнее изменение этой страницы: 2016-07-13; Просмотров: 562; Нарушение авторского права страницы