
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Недостатки АRC – фильтров с имитацией индуктивностей. Принцип позвенной реализации
Если порядок n – четный, то все звенья второго порядка, если нечетный, то есть одно звено первого порядка. Используя аппроксимацию по Баттерворту и Чебышеву, получаем:
Если фильтр –верхних частот, полосовой или заграждающий, надо сделать преобразование частоты в самой передаточной функции и получить выражение для соответствующих звеньев фильтров. Передаточная функция звена ФВЧ 2 порядка
Средняя частота полосового фильтра Чтобы коэффициент передачи на средней частоте равнялся 1, нужно, чтобы Недостатки: При соединении звенья влияют друг на друга. Между ними надо включать развязывающие буферные устройства типа повторителя напряжения (усилитель напряжения с единичным коэффициентом: - ИНУН, у него бесконечно большое входное сопротивление и нулевое выходное). Такое устройство позволяет перемножать коэффициенты передачи, что в данном случае и требуется. Поскольку используются усилители напряжения, решили использовать АRC – фильтры без гираторов, только на усилителях. АRC – фильтры на усилителях
Если коэффициент усиления – вещественный, то говорят ИНУН, если комплексный, то – ПНН. Так как Рассмотрим схемы различных типов фильтров, построенных на операционных усилителях. Усилители напряжения на ОУ: не инвертирующий, единичный и инвертирующий Коэффициент усиления полученного ИНУН определяется соотношением: U2 /U1=(R2+R1)/R1=K Очевидно, что коэффициент усиления всегда больше единицы. Неинвертирующий ИНУН с единичным коэффициентом усиления можно реализовать так, как показано на рисунке. Эту схему называют обычно схемой повторителя напряжения. Инвертирующий ИНУН можно реализовать на ОУ.. Его коэффициент усиления: U2/U1= - R2/R1 =K ФНЧ второго порядка:
ФВЧ: 2 порядка. Здесь емкости не пропускают сигнал с низкой частотой из-за своего большого сопротивления.
Сами усилители можно реализовать с помощью стандартных микросхем ОУ. Условное обозначение операционного усилителя (ОУ) и схема замещения:
RВХ=∞, RВЫХ=0. ФНЧ на операционном усилителе ТU(0)=1, ТU(∞ )=0, n=2. Емкость С1 шунтирует ОУ в обратной связи на высоких частотах и не дает ему усиливать, а С2 шунтирует высоко частотный сигнал перед входом ОУ, что и дает характеристику ФНЧ 2 порядка . Передаточная функция звена второго порядка ФНЧ имеет вид:
В системе из трех уравнений – 5 неизвестных: R1, R2, R3, C1, C2. Чтобы система стала определенной, значением двух любых элементов можно задаться. Положим, например, что R2=R3=1, тогда система уравнений примет вид:
для расчета значений нормированных элементов схемы:
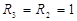 ; ; 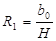 ; ;
Популярное:
|
Последнее изменение этой страницы: 2016-07-13; Просмотров: 604; Нарушение авторского права страницы