
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Смешанное (векторно – скалярное) произведение векторов.
Смешанным произведением векторов ` а, `b, `с называют скалярное произведение вектора ` а ´ `b на вектор ` с, т.е. `а`b`с = (`а ´ `b)`с (1.23) Свойства смешанного произведения: 1) смешанное произведение равно нулю, если: а) хоть один из перемножаемых векторов равен нулю; б) два из перемножаемых векторов коллинеарны; в) перемножаемые векторы компланарны. 2) смешанное произведение не изменится, если знаки векторного и скалярного произведения поменять местами, т.е (`а ´ `b)`с = `а (`b ´ `с). 3) смешанное произведение не меняется, если перемножаемые векторы переставлять в круговом порядке: ` а `b`с = `b`с`а = `с`а `b 4) при перестановке двух любых векторов смешанное произведение меняет знак: ` b`а `с = –`а `b`с; `с `b`а = –`а `b`с; `а `с`b = –`а `b`с Если векторы заданы своими координатами, то:
(Компланарные вектора параллельны одной плоскости; векторное произведение двух векторов даст вектор, перпендикулярный этой плоскости и, соответственно, третьему вектору и их скалярное произведение будет равно нулю). Объемы призмы V1 и пирамиды V2 построенных на ` а, `b, `с определятся так: V1 = |`а `b`с | и V2 = 1 / 6 |`а `b`с | (1.26). Тесты 1. Даны три вектора 1) –32; 2) 14; 3) 48; 4) 32. 2. Даны точки А (3; 1; -1), В (0; 2; -4), С (-2; 1; 3) и Д (-5; 0; 7). Объем пирамиды АВСД численно равен: 1) 8; 2) 3. Какие из векторов 1) 4. Два соседних вектора в смешанном произведении поменяли местами. Что верно? 1) 5. Векторы 1) –7; 2) –8; 3) 7; 4) 8.
5.5 Собственные значения и собственные векторы матрицы. Характеристическим уравнением матрицы Корни Система уравнений
Пример: Найти собственные значения и собственные векторы матрицы: Теперь можно найти собственные векторы матрицы
I.
Используя (1.10) найдём II. (1) - разделим 3-ий столбец на 2, (2) - заменим строки столбцами, (3) - вычтем из 2-ой строки 1-ую, (4 - вычтем из 3-ей строки 2-ую, используя (1.10) найдём: . III. Аналогично вычисляется собственный вектор и для Тесты 1. Характеристическим уравнением матрицы А= 1) 2. Дана матрица А= 1) 2; -3; -6; 2) –2; -3; 6; 3) 2; 3; 6; 4) –2; -3; -6. 3. А = 1) (1; 1); 2) (1; -1); 3) (-1; 1); 4) (4; -5). 4. А = 1) (Х; 3); 2) (Х; Х); 3) (3; 3). 5. Дана диагональная матрица А = 1) Да; 2) Нет.
5.6. Линейные (векторные) пространства. Линейные преобразования. Квадратичные формы. Рассмотрим множество R элементов x, y, z, … для любых Если эти операции удовлетворяют условиям: 1. х+у = у+х; 2. х+(у+z) = (x+y)+z; 3. Существует такой элемент 4. Для каждого 5. 6. 7. 8. то множество Очевидно, что множество геометрических векторов, рассмотренное ранее, является линейным пространством, а предложенное определение расширяет понятие вектора. Линейная независимость векторов определяется через соотношение (1.15), рассмотренное ранее. Максимально возможное число n линейно независимых векторов называют размерностью этого пространства (обозначение: Линейные преобразования. Говорят, что в линейном пространстве R задано преобразование А, если каждому вектору Действия над линейными преобразованиями сводятся к действиям над их матрицами. Например, если вектор Матрица этого линейного преобразования С = ВА. Пример: Даны два линейных преобразования Искомое преобразование С определится произведением А и В Вид матрицы линейного преобразования определяется выбором базиса. Если за базис принять совокупность собственных векторов (см. 1.5.5), то матрица линейного преобразования принимает диагональный вид, причём на главной диагонали стоят собственные значения. Например, в R2 это матрица Квадратичные формы. Квадратичной формой При n=2 при n=3 А = Пусть Переходя к новым координатам получаем квадратичную форму Пример: Привести к каноническому виду уравнение линии 17х2+12ху+8у2=80. В левой части - квадратичная форма с матрицей Тесты 1. Даны две системы четырех действительных чисел: I (а; в; 0; 0), (с; d; 0; 0), (е; f; 0; 0) и II (а; в; 1; 1), (с; d; 1; 1), (е; f; 1; 1). (авсd – всевозможные действительные числа). Является хоть одна из них (если да, то какая) линейным пространством? 2. В линейном пространстве с базисом 1) 3. Каноническая форма уравнения линии 4xy + 3y2 + 16 = 0 имеет вид: 1) Линия на плоскости. Прямая. Всякая линия на плоскости представляет собой совокупность точек. Если известно аналитическое соотношение (формула), связывающее координаты любой (текущей) точки М(х, у), лежащей на этой линии, говорят – линия задана своим уравнением у = f (x) (в общем случае F(x, y) = 0 ). Если в уравнение линии подставить координаты любой ее точки, то уравнение обратится в тождество. Всякое уравнение первой степени (линейное) относительно х и у вида Ах + Ву + С = 0 (1.29), ( А, В, С – постоянные величины, причем А2+ В2 ¹ 0 ) определяет на плоскости некоторую прямую и называется общим уравнением прямой. Рассмотрим частные случаи: 1. А ¹ 0, В ¹ 0, С = 0. Очевидно, что Ах + Ву = 0 – уравнение прямой проходящей через начало координат. 2. А = 0, В ¹ 0, С ¹ 0. Уравнение (1.29) преобразуется к виду у = – С / В = b и определяет прямую параллельную оси Ох (При С = 0 => b = 0 и прямая совпадает с осью Ох ) 3. А ¹ 0, В = 0, С ¹ 0. Уравнение (1.29) принимает вид х = – С /А = а и определяет прямую параллельную оси Оу (При С = 0 => a = 0 и прямая совпадает с осью Оу ) 4. Если В ¹ 0, то, разрешив (1.29) относительно у, получим уравнение вида у = кх + b (1.30) ( к = – А / В, b = – С / В ), называемое уравнением с угловым коэффициентом, ( к = tga, где a – угол между прямой и положительным направлением оси Oх. b – ордината точки пересечения прямой с осью Оу ). 5. Если в (1.29) С ¹ 0, то разделив обе части равенства на - С, получим уравнение вида (х / а) – (у / b) = 1 (1.31) ( а = – С/А; b = – С/В, называемое уравнением прямой в отрезках ( |a| и |b| – длины отрезков, отсекаемых на осях Ох и Оу от начала координат). 6. Умножив обе части (1.29) на Используя предложенные формы уравнений прямой можно получить следующие соотношения: Острый угол между прямыми у = к1х + b1, у = к2х + b2, определится по формуле: Из нее легко получить условие параллельности к1 = к2 (1.34) и перпендикулярности к2 = – 1 / к1 (1.35) прямых. Уравнение прямой, проходящей через точку М0(х0, у0) под заданным углом a к оси Ох (с заданным угловым коэффициентом к = tga ) примет вид у – у0 = к (х – х0) (1.36), а уравнение прямой, проходящей через заданные точки М1(х1, у1) и М2(х2, у2). Найти координаты точки пересечения прямых можно решив систему уравнений, определяющих эти прямые. Расстояние от точки М0(х0, у0) до прямой Ах + Ву + С = 0 определяется по формуле: Деление отрезка в данном отношении. Приведем еще одно соотношение, часто используемое в аналитической геометрии. Проведем прямую через точки А(х1, у1) и В(х2, у2). Всякая третья точка С(х, у) прямой делит отрезок АВ в некотором отношении l = ± АС / СВ (если точка С лежит внутри отрезка АВ, то l > 0, если вне, то l < 0 ). Координаты точки С определяются выражениями: Тесты 1. Общее уравнение прямой имеет вид: 1) 2) 3) y = kx + в; 4) 2. Угол между прямыми определяется выражением: 1) 2) 3. Условия перпендикулярности прямых: 1) 4. Уравнение прямой проходящей через данную точку М (х0, y0) с заданным угловым коэффициентом имеет вид: 1) y – y0 = k (x + x0); 2) y – y0 = k (x - x0); 3) y – х0 = k (x - у0); 4) y0 – х0 = k (у - x). 5. Уравнение прямой, проходящей через точки А(2; -3) и B(-2; 3) имеет вид: 1) Кривые второго порядка. Общее уравнение кривой второго порядка на плоскости хОу имеет вид Ах2 + Вху + Су2 + 2Дх + 2Еу + F = 0 (1.40) (Порядок кривой определяется наивысшей степенью неизвестных, входящих в ее уравнение). Можно показать, что это уравнение описывает либо две пересекающиеся прямые, либо одну из следующих кривых: эллипс, гиперболу или параболу (включая вырожденные случаи). В любом случае кривую можно определить как геометрическое место точек, обладающих некоторым общим свойством. Используя преобразование координат (изменяя расположение кривой по отношению к осям координат) можно сделать так, чтобы в новых координатах уравнение кривой принимало наиболее простую и удобную для анализа форму. Рассмотрим последовательно кривые, именно так расположенные на плоскости хОу. Эллипс. Окружность.
Если фокусы эллипса размещаюся на оси Ох симметрично началу координат в точках F1(c, 0) и F2 (-c, 0) (рис.1.7), то уравнение эллипса примет простейшую (каноническую) форму: где а и b – большая и малая полуоси эллипса, причем а, b, с связаны соотношением а2 = b2 + с2. Форма эллипса (мера сжатия) характеризуется эксцентриситетом Очевидно, что 0 £ е £ 1; е = 1 при b = 0 и эллипс вырождается в отрезок длиной 2а; е = 0 при b = a, когда эллипс вырождается в окружность радиуса а. Расстояния произвольной точки М(х, у) эллипса от его фокусов называются фокальными радиусами – векторами этой точки, обозначаются r1 и r2 и могут быть вычислены по формулам r1 = а – ех (1.43) (правый радиус – вектор) и r1 = а + ех (1.43`) (левый радиус – вектор). При е = 0 (а = b = r) уравнение примет вид х2 + у2 = r2 (1.44) Это уравнение окружности – геометрического места точек равноудаленных от данной точки, называемой центром (в ней «сошлись» фокусы эллипса), с центром в начале координат. Уравнение окружности с центром в заданной точке С(а, b) примет вид (х – а)2 + (у – b)2 = r2 (1.44`) Гипербола. Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а ),
Если фокусы гиперболы расположены на оси Ох симметрично началу координат в точках F1(с, 0) и F2(–с, 0), уравнение гиперболы примет каноническую форму Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А1(а, 0) и А2(–а, 0) называются вершинами гиперболы (рис.1.8). Отрезки А1А2 = 2а и В1В2 = 2b называют действительной и мнимой осями гиперболы. Прямые (Прямая называется наклонной асимптотой кривой, если расстояние между этой прямой и точкой М(х, у) кривой стремится к нулю при стремлении х к ± ¥ (х ® ± ¥ ) ). Величину Фокальные радиусы – векторы определяются соотношениями:
При а = b (e =
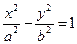 и и 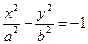 , имеющие одни и те же оси и асимптоты (мнимая ось одной совпадает с действительной осью другой) называют сопряженными. , имеющие одни и те же оси и асимптоты (мнимая ось одной совпадает с действительной осью другой) называют сопряженными.
Парабола. Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если фокус параболы в точке F(р/2, 0), а уравнение директрисы х = –р / 2, то уравнение параболы примет вид у2 = 2рх (1.51). Эта парабола симметрична относительно оси Ох и при р > 0 расположена как на рис. (1.9). х2 = 2ру (1.51`) уравнение параболы, симметричной относительно оси Оу. Фокальный радиус – вектор параболы (1.51) определяется соотношением: r = x + (p / 2) (p > 0) (1.52). Тесты 1. Какое из уравнений описывает кривую второго порядка: 1) х + у + 7 = 0; 3) х2у + 7 = 0; 2) х2 + у + 7 = 0; 4) ху + 2. Уравнение х2 – 2х + у2 + 6у = 0 описывает: 1) Окружность; 2) Эллипс; 3) Гиперболу; 4) Две пересекающихся прямые. 3. Эллипс задан уравнением 1) 4. Уравнение гиперболы 1) 2) 3) 4) 5. Дана парабола у2= -8х. Уравнение ее директрисы имеет вид: 1) х = -4; 2) х = 4; 3) у = -4; 4) у = 4. Популярное:
|
Последнее изменение этой страницы: 2016-08-31; Просмотров: 675; Нарушение авторского права страницы