Линейная оболочка системы векторов. Подпространство. Базис подпространства

Пусть – система векторов из . Линейной оболочкой системы векторов называется множество всех линейных комбинаций векторов данной системы, т.е

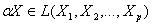Свойства линейной оболочки: Если , то для и .

Линейная оболочка обладает свойством замкнутости по отношению к линейным операциям (операции сложения и умножения на число).

Подмножество пространства , обладающее свойством замкнутости по отношению к операциям сложения и умножения на числа, называется линейным подпространством пространства .

Линейная оболочка системы векторов – линейное подпространство пространства .

Система векторов из называется базисом 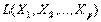, если

Любой вектор можно выразить в виде линейной комбинации базисных векторов:

2. Система векторов линейно независима.

Лемма Коэффициенты 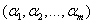разложения вектора по базису определены однозначно.

Вектор , составленный из коэффициентов разложения вектора по базису называется координатным вектором вектора в базисе .

Обозначение . Данная запись подчеркивает, что координаты вектора зависят от базиса.

Линейные пространства

Определения

Пусть дано множество элементов произвольной природы. Пусть для элементов этого множества определены две операции: сложения и умножения на любое вещественное число : , и множество 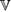замкнуто относительно этих операций: . Пусть эти операции подчиняются аксиомам:

1. для ;

2. для ;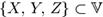

3. в cуществует нулевой вектор со свойством для ;

4. для каждого существует обратный вектор со свойством ;

5. для ;

6. для , ;

7. для , ;

8. для .

Тогда такое множество называется линейным (векторным) пространством, его элементы называются векторами, и — чтобы подчеркнуть их отличие от чисел из — последние называются скалярами ¹⁾. Пространство, состоящее из одного только нулевого вектора, называется тривиальным.

Если в аксиомах 6 - 8 допустить умножение и на комплексные скаляры, то такое линейное пространство называется комплексным. Для упрощения рассуждений всюду в дальнейшем мы будем рассматривать только вещественные пространства.

Линейное пространство является группой относительно операции сложения, причем группой абелевой.

Элементарно доказывается единственность нулевого вектора, и единственность вектора, обратного вектору : , его привычно обозначают .

Подмножество линейного пространства , само являющееся линейным пространством (т.е. замкнуто относительно сложения векторов и умножения на произвольный скаляр), называется линейным подпространством пространства . Тривиальными подпространствами линейного пространства называются само и пространство, состоящее из одного нулевого вектора .

Пример. Пространство упорядоченных троек вещественных чисел

операциями, определяемыми равенствами:

Геометрическая интерпретация очевидна: вектор в пространстве, «привязанный» к началу координат, может быть задан в координатах своего конца . На рисунке показано и типичное подпространство пространства : плоскость, проходящая через начало координат. Точнее говоря, элементами являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения²⁾ очевидна.

Исходя из этой геометрической интерпретации, часто говорят о векторе произвольного линейного пространства как оточке пространства . Иногда эту точку называют «концом вектора ». Кроме удобства ассоциативного восприятия, этим словам не придается никакого формального смысла: понятие «конец вектора» отсутствует в аксиоматике линейного пространства.

Пример. Основываясь на том же примере, можно дать и иную интерпретацию векторного пространства (заложенную, кстати, уже в самом происхождении слова «вектор»³⁾) — оно определяет набор «сдвигов» точек пространства . Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости .

Вообще говоря, с подобными интерпретациями понятия вектора все обстоит не так просто. Попытки аппелировать к его физическому смыслу — как к объекту, имеющему величину инаправление — вызывают справедливую отповедь строгих математиков. Определение же вектора как элемента векторного пространства очень напоминает эпизод с сепульками из знаменитого фантастического рассказа Станислава Лема (см. ☞ ЗДЕСЬ ). Не будем зацикливаться на формализме, а исследуем этот нечеткий объект в его частных проявлениях.

Пример. Естественным обобщением служит пространство : векторное пространство строк или столбцо . Один из способов задания подпространства в 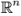— задание набора ограничений.

Пример. Множество решений системы линейных однородных уравнений:

образует линейное подпространство пространства . В самом деле, если

— решение системы, то и

— тоже решение при любом 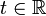. Если

— еще одно решение системы, то и

— тоже будет ее решением.

Почему множество решений системы неоднородных уравнений не образует линейного подпространства?

Пример. Обобщая далее, можем рассмотреть пространство «бесконечных» строк или последовательностей , обычно являющееся объектом математического анализа — при рассмотрении последовательностей и рядов. Можно рассматривать строки (последовательности) «бесконечные в обе стороны» — они используются в ТЕОРИИ СИГНАЛОВ.

Пример. Множество -матриц с вещественными элементами с операциями сложения матриц и умножения на вещественные числа образует линейное пространство.

В пространстве квадратных матриц порядка можно выделить два подпространства: подпространство симметричных матриц и подпространство кососимметричных матриц. Кроме того, подпространства образуют каждое из множеств: верхнетреугольных, нижнетреугольных идиагональных матриц.

Пример. Множество полиномов одной переменной степени в точности равной с коэффициентами из (где — любое из множеств или ) с обычными операциями сложения полиномов и умножения на число из не образует линейного пространства. Почему? — Потому что оно не является замкнутым относительно сложения: сумма полиномов и 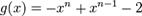не будет полиномом -й степени. Но вот множество полиномов степени не выше

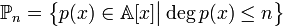
линейное пространство образует; только к этому множеству надо придать еще и тождественно нулевой полином⁴⁾. Очевидными подпространствами являются . Кроме того, подпространствами будут множество четных и множество нечетных полиномов степени не выше . Множество всевозможных полиномов (без ограничения на степени) тоже образует линейное пространство.

Пример. Обобщением предыдущего случая будет пространствополиномов нескольких переменных степени не выше с коэффициентами из . Например, множество линейных полиномов

образует линейное пространство. Множество однородных полиномов(форм) степени (с присоединением к этому множеству тождественно нулевого полинома) — также линейное пространство.

С точки зрения приведенного выше определения, множество строк с целочисленными компонентами

рассматриваемое относительно операций покомпонентного сложения и умножения на целочисленные скаляры, не является линейным пространством. Тем не менее, все аксиомы 1 - 8 будут выполнены если мы допустим умножение только на целочисленные скаляры. В настоящем разделе мы не будем акцентировать внимание на этом объекте, но он довольно полезен в дискретной математике, например в ☞ ТЕОРИИ КОДИРОВАНИЯ. Линейные пространства над конечными полями рассматриваются ☞ ЗДЕСЬ.

Изоморфизм

Пусть имеются два линейных пространства разной природы: с операцией и с операцией . Может оказаться так, что эти пространства «очень похожи», и свойства одного получаются простым «переводом» свойств другого.

Говорят, что пространства и изоморфны если между множествами их элементов можно установить такое взаимно-однозначное соответствие, что если и то и .

При изоморфизме пространств и нулевому вектору одного пространства будет соответствовать нулевой вектор другого пространства.

Пример. Пространство изоморфно пространству 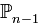. В самом деле, изоморфизм устанавливается соответствием

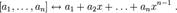
Пример. Пространство -матриц изоморфно пространству . Изоморфизм устанавливается соответствием, которое мы проиллюстрируем для случая :

(матрица «вытягивается» в одну строчку).

Пример. Пространство квадратичных форм от переменных изоморфно пространству симметричных матриц -го порядка. Изоморфизм устанавливается соответствием, которое мы проиллюстрируем для случая :

Понятие изоморфизма вводится для того, чтобы исследование объектов, возникающих в различных областях алгебры, но с «похожими» свойствами операций, вести на примере одного образца, отрабатывая на нем результаты, которые можно будет потом дешево тиражировать. Какое именно линейное пространство взять «для образца»? — См. концовку следующего пункт

Предыдущая 1 2 3 4 5 6 7 8 9 101112 13 Следующая