Среднее квадратическое отклонение
Среднее квадратическое отклонение непрерывной случайной величины определяется точно так же, как и дискретной случайной величины:  .
.
Пример 2. Случайная величина  задана интегральной функцией распределения
задана интегральной функцией распределения  . Требуется:
. Требуется:
1) убедиться, что заданная функция  является функцией распределения некоторой случайной величины, проверив свойства
является функцией распределения некоторой случайной величины, проверив свойства  .
.
В случае положительного ответа найдите:
2) дифференциальную функцию  ;
;
3) математическое ожидание случайной величины  ; дисперсию случайной величины
; дисперсию случайной величины  (двумя способами) и среднее квадратическое отклонение; постройте графики интегральной
(двумя способами) и среднее квадратическое отклонение; постройте графики интегральной  и дифференциальной
и дифференциальной  функций;
функций;
4) вероятность попадания величины  в интервал (
в интервал (  ) двумя способами (используя интегральную и дифференциальную функции), а затем проиллюстрируйте этот результат на графиках
) двумя способами (используя интегральную и дифференциальную функции), а затем проиллюстрируйте этот результат на графиках  и
и  .
.
 ,
,  .
.
Решение:
1) Если функция  является функцией распределения и если возможные значения случайной величины
является функцией распределения и если возможные значения случайной величины  принадлежат интервалу
принадлежат интервалу  , то
, то  , если
, если  ,
,  , если
, если  . Проверим это. По условию
. Проверим это. По условию  , тогда
, тогда  . Таким образом, заданная функция
. Таким образом, заданная функция  является функцией распределения;
является функцией распределения;
2) Дифференциальной функцией распределения  называется производная от интегральной функции:
называется производная от интегральной функции:  .
.
Следовательно, получаем:


 .
.
3) Для вычисления числовых характеристик случайной величины  воспользуемся формулами:
воспользуемся формулами:
–  , где
, где  – плотность вероятности случайной величины
– плотность вероятности случайной величины 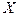 и если возможные значения случайной величины принадлежат отрезку
и если возможные значения случайной величины принадлежат отрезку  ;
;
–  , если возможные значения случайной величины принадлежат отрезку
, если возможные значения случайной величины принадлежат отрезку  ;
;
–  .
.
Вычисляем:  ;
;
 ;
;  ;
;


4) Вычислим вероятность попадания величины  в интервал (
в интервал (  ), используя интегральную функцию
), используя интегральную функцию  : вероятности попадания случайной величины
: вероятности попадания случайной величины  в интервал
в интервал  вычислим по формуле
вычислим по формуле  . В данном случае
. В данном случае  , следовательно
, следовательно  ; дифференциальную функцию
; дифференциальную функцию  :
:  .
.
В данном случае  , т.к.
, т.к.  , если
, если  .
.
6.3. Нормальное распределение непрерывной случайной величины (закон Гаусса)
Распределение вероятностей непрерывной случайной величины 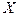 называется нормальным, если плотность вероятности описывается формулой:
называется нормальным, если плотность вероятности описывается формулой:

 ,
,
 где
где  – математическое ожидание,
– математическое ожидание,
 – среднее квадратическое отклонение нормального распределения.
– среднее квадратическое отклонение нормального распределения.
Закон Гаусса имеет большое значение для практического применения по следующим причинам:
1. На практике многие случайные величины оказываются либо нормально распределёнными, либо с распределениями, близкими к нормальному.
2. Случайную величину, не распределённую нормально, часто можно преобразовать таким образом, чтобы она имела распределение, близкое к нормальному.
3. Нормальное распределение может служить аппроксимацией для других распределений, например, для биноминального распределения.
4. При проверке статистических гипотез часто возникают распределения, которые оказываются нормальными.
Вычисление вероятности при нормальном распределении
случайной величины 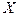
1. Вероятность попадания в интервал  определяется формулой:
определяется формулой:
 ;
;
2. Вероятность попадания в интервал  находим по формуле:
находим по формуле:
 , или
, или  ;
;
3. Вероятность попадания в интервал  находим по формуле:
находим по формуле:
 или
или  ;
;
4. Вероятность того, что отклонение нормально распределенной случайной величины Х от математического ожидания  по абсолютной величине меньше заданного положительного числа
по абсолютной величине меньше заданного положительного числа  равна
равна  , где
, где  – функция Лапласа,
– функция Лапласа,  математическое ожидание,
математическое ожидание,  среднее квадратическое отклонение.
среднее квадратическое отклонение.
Пример 3 . Случайная величина 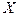 распределена нормально с математическим ожиданием
распределена нормально с математическим ожиданием  . Вероятность попадания
. Вероятность попадания 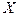 в интервал
в интервал  равна 0, 2. Чему равна вероятность попадания
равна 0, 2. Чему равна вероятность попадания 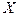 в интервал (35; 40)?
в интервал (35; 40)?
Решение:
1) По известной вероятности попадания 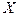 в заданный интервал найдем среднее квадратическое отклонение
в заданный интервал найдем среднее квадратическое отклонение 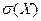 . Для этого воспользуемся формулой
. Для этого воспользуемся формулой  . Согласно условию
. Согласно условию  ,
,  , т.е.
, т.е.
 или
или  , или
, или
 , или
, или  .
.
По таблице значений функции  находим, что
находим, что  , если
, если  , следовательно,
, следовательно,  .
.
1) Вероятность попадания 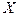 в интервал (35; 40) найдем, используя ту же формулу, тогда
в интервал (35; 40) найдем, используя ту же формулу, тогда

По таблице значений функции  находим, что
находим, что  , а вероятность
, а вероятность  .
.
Упражнения:
Задание 1. Дискретная случайная величина Х может принимать только два значения: x1 и x2, причем x1< x2 . Известны вероятность р1 возможного значения x1 , математическое ожидание М(Х) и дисперсия D(X). Найти закон распределения этой случайной величины.
| Номер задачи
| р1
| М(Х)
| D(X)
|
|
| 0, 1
| 3, 9
| 0, 09
|
|
| 0, 3
| 3, 7
| 0, 21
|
|
| 0, 5
| 3, 5
| 0, 25
|
Задание 2. Задан закон распределения дискретной случайной величины  . Найти: а) неизвестную вероятность; б) математическое ожидание
. Найти: а) неизвестную вероятность; б) математическое ожидание  , дисперсию
, дисперсию  и среднее квадратическое отклонение
и среднее квадратическое отклонение  ; в) составить функцию распределения случайной величины
; в) составить функцию распределения случайной величины  и построить ее график; г) вычислить вероятности попадания случайной величины
и построить ее график; г) вычислить вероятности попадания случайной величины  в интервал
в интервал  , пользуясь составленной функцией распределения
, пользуясь составленной функцией распределения  .
.
1)
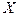
|
|
|
|
|
|

| 0, 1
|
| 0, 1
| 0, 2
| 0, 4
|
2)
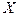
|
|
|
|
|
|

| 0, 2
| 0, 3
| 0, 1
|
| 0, 2
|
3)
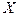
|
|
|
|
|
|

|
| 0, 2
| 0, 2
| 0, 3
| 0, 1
|
4)
|
|
|
|
|
|

| 0, 2
| 0, 3
| 0, 1
| 0, 2
|
|
Задание 3. Случайная величина  задана интегральной функцией распределения
задана интегральной функцией распределения  . Требуется убедиться, что заданная функция
. Требуется убедиться, что заданная функция  является функцией распределения некоторой случайной величины, проверив свойства
является функцией распределения некоторой случайной величины, проверив свойства  . В случае положительного ответа найдите: а) дифференциальную функцию
. В случае положительного ответа найдите: а) дифференциальную функцию  ; в) математическое ожидание случайной величины
; в) математическое ожидание случайной величины  ; c) дисперсию случайной величины
; c) дисперсию случайной величины  и среднее квадратическое отклонение; d) построить графики интегральной
и среднее квадратическое отклонение; d) построить графики интегральной  и дифференциальной f(x) функций.
и дифференциальной f(x) функций.
1)  2)
2) 
3)  4)
4) 
Задание 4.
1) Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины  соответственно равны 20 и 5. Найти вероятность того, что в результате испытания
соответственно равны 20 и 5. Найти вероятность того, что в результате испытания  примет значение, заключенное в интервале
примет значение, заключенное в интервале  .
.
2) В нормальном законе распределения математическое ожидание равно 50, среднеквадратическое отклонение равно 4. Чему равно  , если вероятность того, что случайная величина принимает значение меньше
, если вероятность того, что случайная величина принимает значение меньше  , равна 0.28.
, равна 0.28.
3) Автомат штампует детали. Контролируется длина детали  , которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а)больше 55 мм; б) меньше 40 мм.
, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а)больше 55 мм; б) меньше 40 мм.
Популярное:
- Искусство Древнего Египта. Периоды и особенности развития (Додинастический период, Древнее царство, Среднее царство, Новое царство).
- Любое отклонение от нормы нуждается в консультации специалиста. Чем раньше выявлено нарушение, тем быстрее и легче его удается исправить.
- МАЛОЕ И СРЕДНЕЕ ПРЕДПРИНИМАТЕЛЬСТВО
- Определите среднее списочное число работников за сентябрь
- Показатели размера и интенсивности вариации (размах, среднее линейное отклонение, простое и взвешенное стандартное отклонение, дисперсия для выборки и ГС, коэффициенты осцилляции и вариации).
- Риск как среднее квадратическое отклонение. Бейесовский подход к принятию решений, методы снижения рисков.
- Среднеквадратическое отклонение
- Статическая устойчивость описывает первоначальную реакцию самолёта на отклонение от равновесия относительно одной или более осей (самолёт имеет три оси вращения).
- Структурное среднее: мода, медиана. Принципы выбора сред величин

