
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Уравнение прямой в общем виде.
а) Пусть А=С=0, В Ву=0, следовательно у=0 – ось (ОХ) б) Пусть В=С=0, А Ах=0, следовательно х=0 – ось (ОУ) в) Пусть А=В=0, С 0=С (такого быть не может) г) Пусть А=0, В Ву+С=0, следовательно у=- д) Пусть В=0, А Ах+С=0, следовательно х=-
Ах + Ву = 0 Þ у=
ж) Пусть А¹ 0, В¹ 0, С¹ 0. Ах+Ву = -С Þ у = у = κ х + в, - прямая не проходит через начало координат. Получим, что уравнение Ах+Ву + С = 0 при различных значениях А, В, С содержит в себе все случаи взаимного расположения прямой осей координат. Значит уравнение Ах+Ву + С = 0 - уравнение прямой в общем виде. 2) Уравнение прямой в отрезках.
-
Если х=0Þ у=b; В(0; b). У=0Þ х=а; А(a; 0) Уравнение прямой, проходящей через две точки.
M (x; y) – точка с текущими координатами.
М1М {x-x1; y-y1} M1M2 {x2-x1; y2-y1}.
M1M2 || М1МÞ
Уравнение прямой с заданным нормальным вектором. Вектор Пусть М0 (х0; у0). М (х; у);
A(x-x0)+B(y-y0)=0 Раскроем скобки Ах+Ву+(-Ах0-Ву0)=0 Ах+Ву+С=0 – уравнение прямой в общем виде. Если 2х+3у+5=0Þ -4х+2у-1=0Þ 5) Уравнение прямой с угловым коэффициентом и проходящей через точку М0(х0; у0). А(х-х0)+В(у-у0)=0 В(у-у0)=- А(х-х0) у-у0=- y-y0= κ (x-x0). Уравнение пучка прямых.
считать уравнением пучка прямых при условии, что κ будет меняться. М0(х0; у0) – центр пучка. L0 Tg900 – не существует. Значит в уравнении y-y0=κ (x-x0) не содержит уравнение прямой L0. Ее уравнение будет х=х0, так как κ =tg900 – не существует. Каноническое и параметрическое уравнение прямой.
   Пусть Пусть  {m, n} и {m, n} и  // l. // l.  - направляющий вектор прямой. М0 (х0; у0), М(х; у). М0М {x-x0 ; y-y0}, так как - направляющий вектор прямой. М0 (х0; у0), М(х; у). М0М {x-x0 ; y-y0}, так как  // М0МÞ t // М0МÞ t 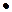 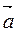 , где t , где t  R (R – множество R (R – множество
действительных чисел)
параметрическое уравнение прямой каноническое уравнение прямой 8) Расстояние от точки до прямой
M0 (x0; y0 )
Ах1+Ву1+С=0 (и) Þ С=-Ах1-Ву1
в) Найдем Из подставим во и получим
Сравним и.
L1: A1x+B1y+C1=0 L2: A2x+B2y+C2=0
тогда | MM1 | = | MM2 | - есть векторы уравнения биссектрисы D1=D2 (Расстояния от точки М (х; у) до прямых L1 и L2 одинаковы).
Пример №1. Написать уравнение биссектрисы угла, образованного прямыми L1, L2, в котороым лежит точка О (0; 0). L1: x1+2y-5=0; L2: 3x-6y+2=0; тогда
Проверим знак прямых L1 и L2 в точке О (0; 0). L1: 0+2
 |x+2y-5|=-(x+2y-5) |x+2y-5|=-(x+2y-5)
|3x-6y+2|=3x-6y+2 - -3x-6y+15=3x-6y+2 Þ 6x-13=0 Уравнение биссектрисы. x=
Ориентация полуплоскости.
если Ах1+Ву1+С > 0, то если Ах2+Ву2+С < 0, то
Пример №2. Найти уравнение биссектрисы 1. Составим уравнение (АС), проходящей через две точки.
аналогично уравнение (АВ): х-3у-14=0 – это (АВ).
Сориентируем L1 и L2 относительно любой точки, находящейся внутри угла ВАС. Этой точкой может быть середина отрезка ВС. М (2, 5; -7, 5) или любая другая точка на прямой ВС.
  L1: 2, 5-3 L1: 2, 5-3 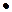 (-7, 5)-14, > 0 Þ |x-3y-14| = x-3y-14 (-7, 5)-14, > 0 Þ |x-3y-14| = x-3y-14
L2: 8
и приведем к виду ( Аналогично можно найти уравнения биссектрис и других внутренних углов этого треугольника. Угловой коэффициент прямой.
k=tg φ * Если φ < 900, то k> 0 Если φ > 900, но φ < 1800, то k< 0 Если φ =900, то k – не существует Если φ =00 или φ =1800, то k=0
t k = Кроме этого в п. 1 мы обозначили k=- ****, **, *** три способа нахождения углового коэффициента прямой. k=tgφ, k = Угол между прямыми.
l1 : A1x+B1y+C1=0, l2 : A2x+B2y+C2=0,
Найдем cos φ = где | Если l1 || l 2, то φ =0 или φ =π Þ cos φ = Если l 1 Если φ < 900, то Þ cos φ > 0 Если 900< φ < 1800, то Þ cos φ < 0 |cos φ |
α 2= α 1+ φ Þ φ = α 2- α 1 tg φ =tg(α 2- α 1) = tg α 2=k2, tg α 1=k1. Тогда tg φ = Формула tg φ, φ образован при повороте прямой l1 вокруг точки В до совмещения с прямой l2 (против часовой стрелки). Если l1||l2, то φ =0 и φ =1800Þ k2=k1 Если l1 т.е. Если l1 Если 900< φ < 1800, то tg φ < 0.
l1 имеет k1 и l2 имеет k2 и l1 : A1x+B1y+C1=0 l2 : A2x+B2y+C2=0 Если l1
 A1x+B1y+C1=0 A1x+B1y+C1=0
A2x+B2y+C2=0 * Если l1||l2, то ** Если l1 Если l1=l2, то * и ** есть условия параллельности и перпендикулярности прямых.
Найдем координаты векторов, которые
AC {x3-x1; y3-y1} По определению векторного произведения векторов (лекция 3 п.1).
 так как так как  =1, то =1, то
SABCD =
SABC=
Пример: А (2; -3) В(4; 2) С(-1; 5)
   а) АВ {2; 5} AC {-3; 8} а) АВ {2; 5} AC {-3; 8}
SABC = Популярное:
|
Последнее изменение этой страницы: 2016-09-01; Просмотров: 1253; Нарушение авторского права страницы