
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Площадь треугольника не зависит от выбора пары векторов
Тема: КРИВЫЕ ВТОРОГО ПОРЯДКА.
Ах2+Ву2+Сху+Dх+Еу+F=0 (*) Окружность. Окружностью называется множество точек плоскости расстояние от каждой из которых до точки, называемой центром, есть величина постоянная, называемая радиусом окружности.
(x-x0)2+(y-y0)2=r2
х2+(y-y0)2=r2 – (ω 1). Если М2(х0; 0), то (х-х0)2+у2=r2 - (ω 2) Если О (0; 0), то х2+у2=r2 – (ω 3).
Покажем, что при условии А=В и С=0 уравнение * есть уравнение окружности. Ах2+Ау2+Dх+Еу+F=0 |: A x2+y2+ (x2+2 (x+ М0 (-
|F1M| + |FM|=2a – векторное уравнение. 2a> 2c
|F1M| = |FM| =
Избавимся от иррациональности и введем величину в2=а2-с2.
Тогда получим уравнение А1; А – вершины эллипса А1 ; А( В1 ; В - вершины эллипса В1 ; В (0; F1 ; F – фокусы эллипса F1 ; F( |А1A|=2a – большая ось эллипса. |BB1|=2в – малая ось эллипса.
  |F1M|=r1 |F1M|=r1
|FM|=r Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси его.
Если е Если е Если е=0, то с=0, следовательно в=а, х2+у2=а2 и с=0, следовательно F1=F=0 – центр окружности. Окружность – есть честный вид эллипса при условии, что, а=в.
е=
то уравнение эллипса будут:
Пример №1.
a2=64, в2=36, в2=а2-с2 а=8; в=6; с=2
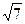
e = Пример №2. Составить уравнение эллипса, если большая ось равна 50, фокусы находятся на оси (ОУ) и е = 0, 6. Так как F1F находятся на оси (ОУ), то:
|BB1| - большая ось эллипса
Получим ГИПЕРБОЛА.
||F1M|-|FM||=2a, 2a< 2c |FF1|=2c - Векторное уравнение гиперболы. Аналогично выводу уравнения эллипса. При условии, что в2= с2-а2.
|AA1|=2a – вещественная ось гиперболы. B; B1 (0; |BB1|=2в – мнимая ось гиперболы. F; F1( |FF1|=2c – фокусное расстояние. (МР) и (NQ) - асимптоты гиперболы. У= Эксцентриситетом гиперболы называется отношение фокусного расстояния и длина вещественной оси гиперболы. е = Если е Если е
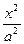 + +  =1, где а2=с2-а2, =1, где а2=с2-а2,
x2-y2=a2(уравнение равносторонней гиперболы), где с2=2а2 e = e= (MN); (NQ): y= Сопряженная гипербола.
где а2= с2-в2, |AA1|=2a – мнимая ось. |BB1|=2в – вещественная ось. F; F1; 0(0; у=
Пример №1. Найти все элементы гиперболы.
a2=36; в2=64; с2= a2+в2=36+64=100; а=6, в=8, с=10, тогда.
|BB1|=16; |AA1|=12; |FF1|=20 Ответ. y= Пример №2. Составить уравнение гиперболы, если ее асимптоты заданы уравнениями у=
Так как точка М1 принадлежит гиперболе, то координаты точки удовлетворяют уравнению гиперболы.
Уравнения и мы решаем системой.
  = = 
ПАРАБОЛА. Параболой называется множество точек плоскости расстояние от каждой из которых до точки, называемой фокусом и прямой, называемой директрисой, равны между собой. Расстояние от фокуса до директрисы |FK|=P и называется параметром параболы.
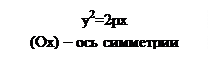
Парабола со смещенной вершиной. Пусть вершиной параболы будет точка А (х0; у0). |KF|=P, точка А делит |KF| напополам. у=у0 – ось симметрии F(x0+ Уравнение параболы (у-у0)2=2р(х-х0). Уравнения остальных парабол со смещенной вершиной будут выглядеть так: (у-у0)2=-2р(х-х0) – ось симметрии || (ОХ), ветви направлены влево. (x-x0)2=
Пример №1.
у2-8у-8х-8=0 у2-8у=8х+8 у2-2·4·у+42=8х+8+42 (у-4)2=8х+24 (у-4)2=8(х+3)
у=4 – ось симметрии ветви параболы вправо.
ЭЛЕМЕНТЫ ВЫСШЕЙ АЛГЕБРЫ. Матрицы.
а11 а12 а13 …..a1n А= a21 a22 a23 …..a2n называется матрицей …………………. am1 am2 am3….amn
Коротко матрица записывается А=(аij) (i=1, 2…m; j=1, 2, …n); Если m=n, то матрица называется квадратной Если m
а1 а2 Если m> 1, n=1, то А=.. - одностолбцовая матрица .. am Действия над матрицами. Сложение матрицы с одинаковым количеством строк и одинаковым количеством столбцов можно складывать. Причем: аij А
2 3 4 -1 4 -2 2+(-1) 3+4 4+(-2) 5 7 -1 + 3 -1 0 = 5+3 7+(-1) -1+0 = 8 9 -5 -5 3 2 8+(-5) 9+3 -5+2
1 7 2 = 8 6 -1 3 12 -3
Умножение на число. При умножении матрицы на число, все ее элементы умножаются на это число.
2 3 4 2∙ 5 3∙ 5 4∙ 5 10 15 20 5∙ 5 7 -1 = 5∙ 5 7∙ 5 -1∙ 5 = 25 35 -5 8 9 -5 8∙ 5 9∙ 5 -5∙ 5 40 45 -25
Умножение матриц. Произведением матрицы А=(aij), имеющей m строк и k столбцов, на матрицу B=(вij), имеющую k строк и n столбцов, называется матрица С=(сij), имеющая m строк и n столбцов, у которого элемент cij равен сумме произведений элементов i-ой строки матрицы А и j-го столбца матрицы В, то есть сij=ai1∙ в1j+ai2∙ в2j+…+aik∙ вkj, (i=1, 2…m; j=1, 2, …n). Причем k столбцов матрицы А должно быть равно числу строк матрицы В. В противном случае произведение неопределено.
1 3 -4
5 6 7 -2 4 3
5∙ 1+6∙ 5+7∙ (-2) 5∙ 3+6∙ (-3)+7∙ 4 5∙ (-4)+6∙ 2+7∙ 3 21 18 13 Определение: Матрица, у которой элементы, стоящие на главной диагонали равны единицы, называются единичной матрицей и обозначается Е.
………………………….. 0 0 0.. 1 А – квадратная и Е – квадратная с тем же количеством строк и столбцов что и А . Каждой матрице соответствует свой определитель ( ДЕТЕРМИНАНТ ).
А= a2 в2 с2 а3 в3 с3а3 в3 с3
Теория матриц и определителей имеет широкое применение как в самой математике, так и в её приложениях. Это очень удобный и часто используемый в самых разнообразных исследованиях математический аппарат. Рассмотрим применение матриц и определителей к исследованию и решению системы трех линейных уравнений первой степени с тремя неизвестными.
a2x+в2y+c2z=d2 a3x+в3y+c3z=d3 Упорядоченная тройка чисел (x0; y0; z0) является решением системы, если в результате подстановки этих чисел в систему вместо x, y, z все три уравнения обращаются в верные равенства. Геометрически каждое уравнение системы - есть плоскость. Три плоскости в пространстве могут располагаться следующим образом: 1. Все три плоскости пересекаются в точке M0 (x0; y0; z0) – координаты этой точки и есть решение системы. Система будет иметь единственное решение. 2. Все три плоскости параллельны или две из них параллельны, а третья пересекает их, или совпадает с одной из них. Тогда общих точек плоскостей нет. Система не будет иметь решений. 3.
Для решения системы алгебраически составим определители.
а3 в3 с3 d3 в3 с3
а3 d3 с3 а3 в3 d3
1. Если ∆ х= Это формулы Крамера (Швейцарский математик). 2. Если ∆ =0, ∆ х 3. Если ∆ =∆ x∆ y=∆ z=0, то система имеет бесконечное множество решений.
a2x+в2у+с2z=0 называется однородной системой а3x+в3у+с3z=0 Эта система всегда имеет решение М0(0; 0; 0). Популярное:
|
Последнее изменение этой страницы: 2016-09-01; Просмотров: 613; Нарушение авторского права страницы