
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ И ЕЕ УРАВНЕНИЯ.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ИСОВСКИЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ ТЕХНИКУМ»
Методические рекомендации по самостоятельной работе студентов по
дисциплине “ МАТЕМАТИКА ”
для заочного отделения по специальности «Техническое обслуживание и ремонт автомобильного транспорта»
Нижняя Тура
Составитель: Л.Н.Фот – преподаватель общеобразовательных, математических и естественно – научных дисциплин.
Пояснительная записка
Рекомендации по самостоятельной работе студентов составлены в соответствии с рабочей программой автора Л.Н.Фот от 2009 года. Внеаудиторная самостоятельная работа студентов по дисциплине математика составляет 37 часов. Самостоятельная работа предусмотрена по основным разделам дисциплины, пропорционально аудиторной нагрузке. В рекомендациях предложен краткий теоретический материал, разобраны решения заданий по разделам дисциплины, а так же задания для контрольной работы, вопросы для зачёта. Характер работ, предложенных студентам, разнообразен, так как имеет разные цели: первичное овладение знаниями, усвоение нового материала, закрепление и систематизация знаний, применение знаний, формирование умений. Студентам предлагаются следующие виды заданий: чтение и конспектирование дополнительной и справочной литературы; работа со словарями и справочниками; решение задач по образцу. Внеаудиторная самостоятельная работа рассчитана на самостоятельное выполнение студентом, с использованием конспекта лекций по дисциплине, учебников, справочников и учебных пособий.
Программа по математике МЕТОД КООРДИНАТ. Векторный базис на плоскости. Прямоугольные координаты. Формулы преобразования прямоугольных координат. Расстояние между двумя точками на плоскости. Деление отрезка в данном соотношении. Полярные координаты. Связь между полярными и прямоугольными координатами. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ И ЕЕ УРАВНЕНИЯ. Понятие об уравнении линии на плоскости. Общее уравнение прямой. Уравнение прямой, проходящей через две точки. Уравнение прямой, проходящей через данную точку. Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом. Уравнение пучка прямых. Параметрическое уравнение прямой. Каноническое уравнение прямой. Ориентация плоскости. Расстояние от точки до прямой. Уравнение биссектрисы. Угол между прямыми. Условие параллельности перпендикулярности прямых. КРИВЫЕ ВОРОГО ПОРЯДКА. Уравнение второй степени с двумя неизвестными. Окружность. Эллипс. Гипербола. Парабола. Кривые второго порядка как конические сечения. Исследование общего уравнения прямой второго порядка. ЭЛЕМЕНТЫ ВЫСШЕЙ АЛГЕБРЫ Матрицы. Свойства матриц. Действия над матрицами. Определители второго порядка. Решение и исследования систем линейных уравнений с помощью определителей. Определители третьего порядка. Решение и исследование систем линейных уравнений с помощью определителей. Решение систем линейных уравнений матричным способом. Понятие обратной матрицы. ВЕКТОРНАЯ АЛГЕБРА. Понятие вектора. Действия над векторами. Координаты в пространстве. Координаты вектора на плоскости и в пространстве. Действия над векторами в координатах разложения вектора по ортам. Скалярные произведение двух векторов и его свойства. Векторное произведение двух векторов и его свойства. Смешанное произведение трех векторов и его свойства. ПЛОСКОСТЬ. ПРЯМАЯ В ПРОСТРАНСТВЕ. Векторное и нормальное уравнение плоскости. Угол между двумя плоскостями. Расстояние от точки до плоскости. Условия параллельности и перпендикулярности плоскостей. Уравнение плоскости, проходящей через три точки. Связка плоскостей. Пучок плоскостей. Условия параллельности и перпендикулярности прямой и плоскости. Уравнение прямой в пространстве. Условия компланарности двух прямых. Прямая как линия пересечения двух плоскостей, приведение её уравнения к каноническому виду. Решение задач на плоскость и прямую. ТЕОРИЯ ПРЕДЕЛОВ. Функция. Способы задания функций. Взаимно обратные функции наложение функциональных зависимостей. Сложная функция. Основные свойства функции. Приращение аргумента, функции. Бесконечная числовая последовательность и её предел. Предел функции. Бесконечно малые величины. Свойства Бесконечно малых величин. Связь Бесконечно малых и Бесконечно больших величин. Теоремы о пределах. Признаки существования предела. Два замечательных предела. Сравнение бесконечно малых величин. Непрерывность функции в точке. Свойства непрерывных функций. Использование непрерывности функций при вычисление предела. Точки разрыва функции. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ. Определение производной функции. Непрерывность и дифференцируемость функции. Правила дифференцирования. Формулы дифференцирования элементарных функций. Дифференцирование неявных функций. Дифференцирование функций, заданных параметрически. Дифференциал функции. Дифференциалы высших порядков. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ. Монотонность функции. Экстремумы функции. Наибольшее, наименьшее значения функции. Теоремы Ферма, Ролля, Лагранжа, Коши. Правило Лопиталя для раскрытия неопределенностей. Признаки возрастания и убывания функции и экстремумов функции. Выпуклость, вогнутость графика. Точка перегиба графика. Второе правило отыскания экстремума функции. Асимптоты графика. Построение графика функции. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ. Физический смысл производной первого и второго порядка. Геометрический смысл производной. Уравнение касательной и нормали к графику кривой. Дифференциал дуги. Кривизна плоской кривой. Векторная функция скалярного аргумента и её дифференцирование. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ. Понятие первообразной функции. Основная теорема первообразной. Понятие о не определенном интеграле. Таблица интегралов, табличное интегрирование. Общие методы интегрирования. Различные способы интегрирования. Понятие об определенном интеграле. Основные свойства определенно интеграла. Определенный интеграл с переменными пределами. Приемы вычисления определенно интеграла. Приближенное вычисление определенного интеграла. Геометрический смысл определенно интеграла. Приложение определенного интеграла к решению геометрических и физических задач. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Функция нескольких переменных. Предел функции. Непрерывные функции. Функция нескольких независимых переменных. Предел функции. Частные производные и частные дифференциалы. Полный дифференциал функции. Дифференцирование сложной и неявной функции. Производная в данном направлении. Градиент функции. ДВОЙНОЙ ИНТЕГРАЛ. ТРОЙНОЙ ИНТЕГРАЛ. Двойной интеграл, его основные свойства. Теорема о среднем. Вычисление двойного интеграла. Приложение двойного интеграла к решению задач. Тройные интегралы. Вычисление тройных интегралов. РЯДЫ. Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда. Свойства сходящихся и расходящихся рядов. Признаки сходимости ряда. Знакопеременные ряды. Функциональный ряд; область сходимости. Степенной ряд; промежуток сходимости. Разложение функции в степенной ряд. Примеры вычисления с помощью степенных рядов. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Понятие о дифференциальном уравнении. Дифференциальное уравнение первого порядка. Дифференциальное уравнение второго порядка. Линейные дифференциальные уравнения. Однородные дифференциальные уравнения. КОМПЛЕКСНЫЕ ЧИСЛА Развитие понятия числа. Комплексные числа. Свойства комплексных чисел. Действия над комплексными числами. Мнимая единица. Степени мнимой единицы. Формы комплексного числа (алгебраическая, геометрическая, тригонометрическая, показательная). Переход из одной формы к другим. Действия над комплексными числами в различных формах. Решение уравнений на множестве комплексных чисел. Метод координат. В аналитической геометрии геометрические объекты – кривые и поверхности – изучаются при помощи алгебры. В основе такого изучения лежит метод координат, при котором положение точки на прямой плоскости или в пространстве определяется соответственно одним, двумя или тремя числами, координатами этой точки, а каждой кривой или поверхности соответствует одно или несколько уравнений, связывающих координаты всякой точки им принадлежащей.
 Подставим в уравнение. Подставим в уравнение.
½ =1/2*12(u) координаты точки M удовлетворяют уравнению y=(1/2)*x2
Определение. Ординатой точки называют расстояние этой точки до оси (OX). Ордината положительна, если точка расположена выше оси (OX), отрицательна, если точка ниже оси (OX).
Деление отрезка в заданном соотношении.
Выразим вектор
Из (2) подставим в (1)
Из
(5) поместим рисунок в систему координат так, чтобы точка О стала центром системы, тогда Равенство (5) является векторной формулой деления отрезка в данном отношении.
*
Формулы координат точки С, делящей отрезок АВ в отношении
Медианы в точке пересечения делятся в отношении
Задача 2. До какой точки надо продлить отрезок АВ(от А к В) чтобы длина его стала в четыре раза больше прежней.
Тогда по формулам **
Теорема. Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические заполнения.
Пример.
=
ВЕКТОРЫ В ПРОСТРАНСТВЕ. Определение вектора, действия над векторами, виды векторов, способы задания векторов на плоскости и в пространстве аналогичны. ОПРЕДЕЛЕНИЕ: Векторы, принадлежащие одной плоскости после сведения их к одному началу, называются компланарными. {
Определение: Векторы М Z –аппликата точки М. Во всех формулах, полученных в лекции №1, добавляется третья координата. 1. 2.
=0
УРАВНЕНИЕ ЛИНИИ Определение: Уравнение с двумя неизвестными f(x; y)=0 являются уравнением линии, тогда и только тогда, когда координаты всех точек этой линии удовлетворяют уравнению этой линии, а координаты точек не принадлежащих этой линии не удовлетворяют уравнению. х2+у2=25 т. М1(3; 4) – удовлетворяют уравнению, значит точка М1 – принадлежит графику М2 (2; -1) – не принадлежит линии. УРАВНЕНИЕ ПРЯМОЙ Прямая линия есть простейшая из кривых на плоскости. Задав на плоскости систему координат, положение любой прямой на координатной плоскости можно определить различными способами, т.е. при помощи различных параметров. В зависимости от выбора этих параметров, определяющих положение прямой на плоскости, мы получим несколько видов уравнений прямой, которые будут полезны при решении различных типов задач. Уравнение пучка прямых.
считать уравнением пучка прямых при условии, что κ будет меняться. М0(х0; у0) – центр пучка. L0 Tg900 – не существует. Значит в уравнении y-y0=κ (x-x0) не содержит уравнение прямой L0. Ее уравнение будет х=х0, так как κ =tg900 – не существует. Ориентация полуплоскости.
если Ах1+Ву1+С > 0, то если Ах2+Ву2+С < 0, то
Пример №2. Найти уравнение биссектрисы 1. Составим уравнение (АС), проходящей через две точки.
аналогично уравнение (АВ): х-3у-14=0 – это (АВ).
Сориентируем L1 и L2 относительно любой точки, находящейся внутри угла ВАС. Этой точкой может быть середина отрезка ВС. М (2, 5; -7, 5) или любая другая точка на прямой ВС.
  L1: 2, 5-3 L1: 2, 5-3 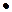 (-7, 5)-14, > 0 Þ |x-3y-14| = x-3y-14 (-7, 5)-14, > 0 Þ |x-3y-14| = x-3y-14
L2: 8
и приведем к виду ( Аналогично можно найти уравнения биссектрис и других внутренних углов этого треугольника. Угловой коэффициент прямой.
k=tg φ * Если φ < 900, то k> 0 Если φ > 900, но φ < 1800, то k< 0 Если φ =900, то k – не существует Если φ =00 или φ =1800, то k=0
t k = Кроме этого в п. 1 мы обозначили k=- ****, **, *** три способа нахождения углового коэффициента прямой. k=tgφ, k = Угол между прямыми.
l1 : A1x+B1y+C1=0, l2 : A2x+B2y+C2=0,
Найдем cos φ = где | Если l1 || l 2, то φ =0 или φ =π Þ cos φ = Если l 1 Если φ < 900, то Þ cos φ > 0 Если 900< φ < 1800, то Þ cos φ < 0 |cos φ |
α 2= α 1+ φ Þ φ = α 2- α 1 tg φ =tg(α 2- α 1) = tg α 2=k2, tg α 1=k1. Тогда tg φ = Формула tg φ, φ образован при повороте прямой l1 вокруг точки В до совмещения с прямой l2 (против часовой стрелки). Если l1||l2, то φ =0 и φ =1800Þ k2=k1 Если l1 т.е. Если l1 Если 900< φ < 1800, то tg φ < 0.
l1 имеет k1 и l2 имеет k2 и l1 : A1x+B1y+C1=0 l2 : A2x+B2y+C2=0 Если l1
 A1x+B1y+C1=0 A1x+B1y+C1=0
A2x+B2y+C2=0 * Если l1||l2, то ** Если l1 Если l1=l2, то * и ** есть условия параллельности и перпендикулярности прямых.
Найдем координаты векторов, которые
AC {x3-x1; y3-y1} По определению векторного произведения векторов (лекция 3 п.1).
 так как так как  =1, то =1, то
SABCD =
SABC=
Пример: А (2; -3) В(4; 2) С(-1; 5)
   а) АВ {2; 5} AC {-3; 8} а) АВ {2; 5} AC {-3; 8}
SABC = ГИПЕРБОЛА.
||F1M|-|FM||=2a, 2a< 2c |FF1|=2c - Векторное уравнение гиперболы. Аналогично выводу уравнения эллипса. При условии, что в2= с2-а2.
|AA1|=2a – вещественная ось гиперболы. B; B1 (0; |BB1|=2в – мнимая ось гиперболы. F; F1( |FF1|=2c – фокусное расстояние. (МР) и (NQ) - асимптоты гиперболы. У= Эксцентриситетом гиперболы называется отношение фокусного расстояния и длина вещественной оси гиперболы. е = Если е Если е
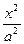 + +  =1, где а2=с2-а2, =1, где а2=с2-а2,
x2-y2=a2(уравнение равносторонней гиперболы), где с2=2а2 e = e= (MN); (NQ): y= Сопряженная гипербола.
где а2= с2-в2, |AA1|=2a – мнимая ось. |BB1|=2в – вещественная ось. F; F1; 0(0; у=
Пример №1. Найти все элементы гиперболы.
a2=36; в2=64; с2= a2+в2=36+64=100; а=6, в=8, с=10, тогда.
|BB1|=16; |AA1|=12; |FF1|=20 Ответ. y= Пример №2. Составить уравнение гиперболы, если ее асимптоты заданы уравнениями у=
Так как точка М1 принадлежит гиперболе, то координаты точки удовлетворяют уравнению гиперболы.
Уравнения и мы решаем системой.
  = = 
ПАРАБОЛА. Параболой называется множество точек плоскости расстояние от каждой из которых до точки, называемой фокусом и прямой, называемой директрисой, равны между собой. Расстояние от фокуса до директрисы |FK|=P и называется параметром параболы.
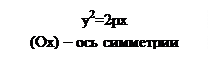
Популярное:
|
Последнее изменение этой страницы: 2016-09-01; Просмотров: 1254; Нарушение авторского права страницы