Закон Пуассона: вероятности, числовые характеристики, функция распределения.
N независимых испытаний, причем n достаточно велико, в каждом из к.вер-ть наступления события А равна р, причем р достаточно мало (р< =0, 1). Пусть СВ Х – число наступлений события А в n испытаниях. Тогда значение Х изменяется от 0 до 1, а вер-ть находится по ф-ле
Рn(k) = (λ k * e-λ )/k! , λ = n*p
Числовые хар-ки:
М(Х) = D(x) = λ
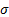 (X) =
(X) = 
M0(X) – мода – значение величины, плотность вер-ти к.максимальна
Ме(Х) – медиана – значение, при к. Р(X< Me) = P(X> Me)
As =  – ассиметрия
– ассиметрия
Ех(Х) = =  – 3 – эксцесс
– 3 – эксцесс
Моменты:
1)начальный
 =
= 
б)центральный

ФР:
F(x) = P(X< x)
10. Геометрический закон распределения: вероятности, числовые характеристики, функция распределения.
Проводится m испытаний до 1го появления X. вер-ть наступления события А = p
P(m) = pqm-1
M(X) = 1/p
D(X) = q/p2
 (X) =
(X) = 
M0(X) – мода – значение величины, плотность вер-ти к.максимальна
Ме(Х) – медиана – значение, при к. Р(X< Me) = P(X> Me)
As =  – ассиметрия
– ассиметрия
Ех(Х) = =  – 3 – эксцесс
– 3 – эксцесс
Моменты:
1)начальный
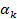 =
= 
б)центральный

ФР:
F(x) = P(X< x)
11. Непрерывные случайные величины, плотность распределения и ее свойства, числовые характеристики, функция распределения и ее свойства НСВ.
Непрерывной СВ назыв.величина, к.м/принимать любые значения из некоторого конечного или бесконечного промежутка. Число значений НСВ явл.бесконечным.
Функция распределения График ФР
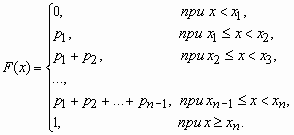
 (cтрелочки влево)
(cтрелочки влево)
Св-ва ФР:
1)0< =F(x)< =1
2) 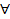 x2> x1 F(x2)> =F(x1)
x2> x1 F(x2)> =F(x1)
3)P(a< =X< =b) = F(b) – F(a)
4)F(+  ) = 1
) = 1
F(-  ) = 0
) = 0
Плотность распределения
f(x) = F’(x)
Св-ва f(x):
1) 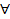 x f(x)> =0
x f(x)> =0
2)  = F(+
= F(+  )
)
3)вер-ть попадания в интервал
Р(a< X< b) = F(b)-F(a) = 
Числовые хар-ки
М(Х) = 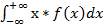
D(x) =  =
=  – (M(X))2
– (M(X))2
 (X) =
(X) = 
Момент
1)начальный

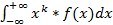
2)центральный

As =  – ассиметрия
– ассиметрия
Ех(Х) = =  – 3 – эксцесс
– 3 – эксцесс
мода М0(Х) = max f(x)
медиана Ме(Х) – абсцисса точки, в к.площадь, ограниченная плотностью распределения, делится пополам.
12. Показательный закон распределения: плотность распределения, числовые характеристики, функция распределения.
Показательное распределение – распределение НСВ, если ее плотность распределения имеет вид
f(x) = 
 F(x) =
F(x) = 
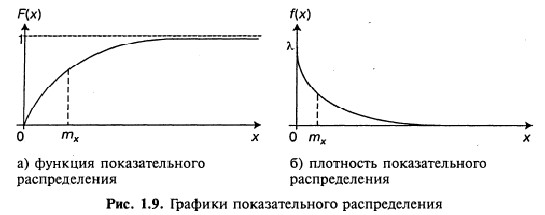
Числовые хар-ки:
М(х) = 1/λ
D(X) = 1/λ 2

Момент
1)начальный

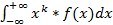
2)центральный

As =  – ассиметрия
– ассиметрия
Ех(Х) = =  – 3 – эксцесс
– 3 – эксцесс
мода М0(Х) = max f(x)
медиана Ме(Х) – абсцисса точки, в к.площадь, ограниченная плотностью распределения, делится пополам.
13. Нормальный закон распределения: плотность распределения, числовые характеристики, функция распределения.
НСВ распределена по нормальному закону, если ее плотность распределения имеет вид:
f(x) =  *
* 
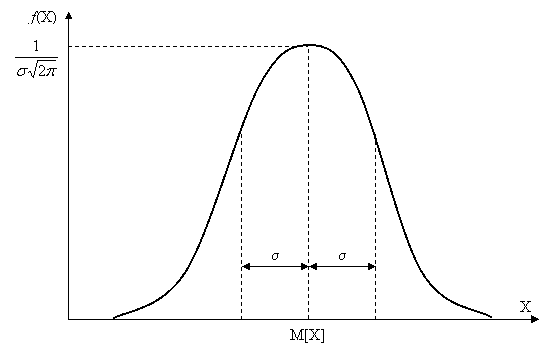
Числовые хар-ки
М(Х) = а
D(X) = 

Момент
1)начальный

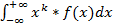
2)центральный
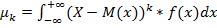
As =  – ассиметрия
– ассиметрия
Ех(Х) = =  – 3 – эксцесс
– 3 – эксцесс
мода М0(Х) = max f(x)
медиана Ме(Х) – абсцисса точки, в к.площадь, ограниченная плотностью распределения, делится пополам.

14. Системы ДСВ. Двумерные ДСВ, закон распределения, числовые характеристики систем, функция распределения и ее свойства.
Двумерную случайную величину обозначают ( X, Y ). Каждую из величин X и Y называют составляющей; обе величины X и Y , рассматриваемые одновременно, образуют систему двух случайных величин.
Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т. е. пар чисел 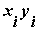 и их вероятностей p
и их вероятностей p  . Обычно закон распределения задают в виде таблицы.
. Обычно закон распределения задают в виде таблицы.
Свойства функции распределения двумерной случайной величины
1. Значения функции распределения удовлетворяют неравенству:
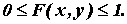
2. F(x, y) есть неубывающая функция по каждому аргументы, т.е.:
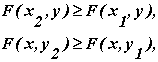
если  и
и 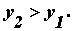
3. Имеют место предельные соотношения:
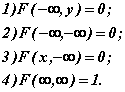
4. При  функция распределения двумерной случайной величины становится функцией распределения составляющей X:
функция распределения двумерной случайной величины становится функцией распределения составляющей X:
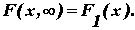
При 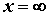 функция распределения двумерной случайной величины становится функцией распределения составляющей Y:
функция распределения двумерной случайной величины становится функцией распределения составляющей Y:

Числовые хар-ки систем
M(X) = 
D(X) = 
Начальный момент  = M(Xk, Ys)
= M(Xk, Ys)
Центральный момент 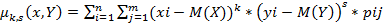
15. Системы НСВ. Двумерные НСВ, плотность распределения и ее свойства, числовые характеристики систем.
Двумерную случайную величину обозначают (X, Y). Каждую из величин X и Y называют составляющей; обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т. е. пар чисел (xi, yi) и их вероятностей p(xi, yi). Обычно закон распределения задают в виде таблицы.
Двумерная СВ назыв.непрерывной, если ее ФР F(X, Y) явл.непрерывной ф-цией, дифференцируемой по каждому из аргументов и сущ-вует 2я смешанная производная этой ф-ции. Плотность распределения двумерной СВ назыв.2я смешанная производная от ФР
f(X, Y) = F’’xy(XY)
Св-ва плотности НДСВ
1) 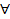 x, y f(x, y)> =0
x, y f(x, y)> =0
2)P((X, Y)  D) =
D) = 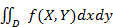 – вер-ть попадания в область D|
– вер-ть попадания в область D|
3)F(X, Y) = 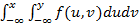
4)  = 1
= 1
5) 
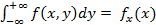
Числовые хар-ки систем
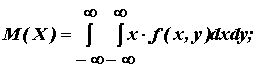
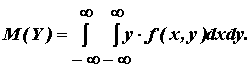

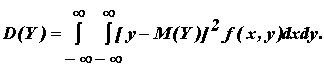
Начальный момент  = M(Xk, Ys)
= M(Xk, Ys)
Центральный момент  =
= 
16. Зависимость и независимость двух СВ. Условные законы распределения двумерных СВ. Коэффициент корреляции, корреляционный момент, их свойства.
СВ Х и У назыв.независимыми, если независимы события {X< x} и {Y< y}, иначе СВ назыв.зависимыми.
Если Х и У зависимы между собой, то для хар-ки их зависимости вводится понятие условных ЗР. Условным ЗР СВ, входящей в систему (Х, У), назыв.её ЗР, найденный при у-вии, что другая СВ приняла определенное значение или попала в определенный интервал.
условным законом распределения СВ Y при условии  называется совокупность вероятностей
называется совокупность вероятностей

Аналогично определяется закон распределения ДСВ X при условии 
Корреляционным моментом/ковариацией 2х СВ Х и У назыв.центральный момент первого порядка от (Х, У)
cov(X, Y) =  = M(XY)-M(X)*M(Y)
= M(XY)-M(X)*M(Y)
Св-ва ковариации:
1) cov(X, Y) = cov (Y, X)
2) cov(X, X) = D(X)
3)Х и У независимы => cov(X, Y) = 0
4)D(X+-Y) = D(X)+D(Y)+-2cov(X, Y)
5) cov(X+C, Y) = cov(X, Y)
cov(X, Y+C) = cov(X, Y)
cov(X+C, Y+C) = cov(X, Y)
6) cov(X, Y)< = 
Коэффициент корреляции
 =r(X, Y)
=r(X, Y)
Св-ва коэффициента корреляции
1)-1< =  < = 1
< = 1
2)X и У независимы =>  =0
=0
3)Х и У связаны линейной зависимостью
У = aX+b
|  | = 1
| = 1
Если a> 0=>  = 1; если a< 0=>
= 1; если a< 0=>  =-1
=-1
4) Чем ближе |  | к 1, тем теснее линейная связь между переменными Х и У
| к 1, тем теснее линейная связь между переменными Х и У
линейная связь:
0< =|  |< =0, 25 – слабая
|< =0, 25 – слабая
0, 25< =|  |< =0, 5 – умеренная
|< =0, 5 – умеренная
0, 5< =|  |< =0, 75 – средняя
|< =0, 75 – средняя
0, 75< =|  |< =0, 9 - сильная
|< =0, 9 - сильная
0, 9< =|  |< =1 – очень сильная
|< =1 – очень сильная
17. Функции СВ одного случайного аргумента.
Пусть рассматриваются две СВ X и Y, связанные функциональной зависимостью 
Если X – ДСВ, закон распределения которой определяется формулой  то Y – ДСВ, а ее закон распределения выражается формулой
то Y – ДСВ, а ее закон распределения выражается формулой  где
где  ,
, 
Математическое ожидание и дисперсия СВ Y определяются соответственно равенствами:


Если X – НСВ с плотностью распределения  и если
и если  – дифференцируемая и монотонная функция, то плотность распределения
– дифференцируемая и монотонная функция, то плотность распределения 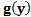 СВ
СВ  выражается формулой
выражается формулой  , где
, где 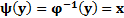 – функция, обратная функции
– функция, обратная функции 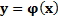 (эта функция существует в силу монотонности
(эта функция существует в силу монотонности  )
)
Если функция  немонотонная, то числовая прямая разбивается на n промежутков монотонности и обратная функция
немонотонная, то числовая прямая разбивается на n промежутков монотонности и обратная функция  находится на каждом из них; плотность распределения
находится на каждом из них; плотность распределения 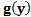 СВ
СВ  определяется в этом случае по формуле
определяется в этом случае по формуле 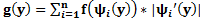
Для нахождения математического ожидания и дисперсии СВ  необязательно находить ее закон распределения; можно воспользоваться формулами:
необязательно находить ее закон распределения; можно воспользоваться формулами:


Популярное:

