
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Неразрывность потока. Уравнение Бернулли
В предыдущих параграфах (3.4., 4.1.) при описании вещества в модели сплошной среды нами рассматривались две простейшие ситуации. Либо мы имели дело с движением специфической «квазичастицы» индивидуального типа – малого элемента объёма среды DV, состоящего из одних и тех же атомов, вблизи фиксированного положения равновесия. При этом нам удалось получить достаточно подробное описание малых отклонений параметров среды от их равновесных значений с течением времени; например, уравнение волны. Либо мы рассматривали сохраняющиеся физические величины, присущие сплошной среде, для одного и того же фиксированного конечного элемента объёма DV независимо от того, какие атомы находились в нём в заданный момент времени. При таком подходе удалось получить некоторые представления о свойствах сплошной среды в целом, атомы которой способны совершать произвольное поступательное движение. В частности, это относится к плотности и давлению сплошной среды. Из всего сказанного следует, важнейшая особенность макроскопических элементов сплошной среды как «частиц» состоит в том, что они не могут двигаться независимо. Любое их движение должны быть таким, чтобы не разрушить целостность среды. Для выяснения условия, обеспечивающего «непрерывность» сплошной среды, полезно обратиться к закону сохранения массы, справедливому в нерелятивистском приближении; скорость движения элементов среды
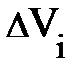
Пусть у нас есть изолированный макроскопический объект сплошной среды (жидкости или газа) объёмом 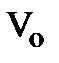 (рис. 4.5. а), полная масса которого М постоянная (равна const). Разобьём его мысленно на элементы объёма (рис. 4.5. а), полная масса которого М постоянная (равна const). Разобьём его мысленно на элементы объёма 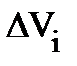 , имея в виду, что , имея в виду, что 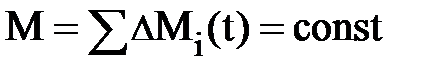 (рис. 4.5. а); здесь (рис. 4.5. а); здесь 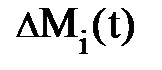 – переменная масса, заключённая в объёме – переменная масса, заключённая в объёме 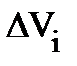 , причём , причём 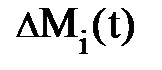 = r(r, t)× = r(r, t)× 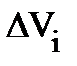 . Будем считать, что плотность вещества в элементе . Будем считать, что плотность вещества в элементе 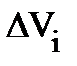 равна плотности макроскопического объекта сплошной среды, равна плотности макроскопического объекта сплошной среды, 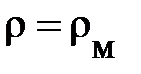 . .
Поскольку масса Если плотность среды со временем не изменяется, сплошная среда называется стационарной. В стационарном случае вводят понятие трубки тока. Ею называется всякий объём сплошной среды (жидкой или газообразной), боковые стенки которого (рис. 4.6.) образованы линиями тока. Трубка тока выделена тем, что вдоль её боковой поверхности всюду скорость перпендикулярна площади потока S. При этом поток через боковую поверхность отсутствует (рис. 4.6.). В этом случае смысл закона неразрывности потока прост – вдоль трубки тока расход стационарной среды не изменяется и модуль скорости всегда обратно пропорционален сечению трубки тока.
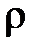 = const; (разумеется, для газов такое предположение несправедливо). При таком приближении речь может идти только о рассмотрении поступательного движения элемента жидкости во внешних потенциальных полях сил. К их числу относятся как объёмные силы, в частности, гравитационные, действующие на каждую частицу жидкости, так и упругие силы, вызываемые давлением на элемент жидкости в целом со стороны стенок сосуда. В этом предельном случае роль сохраняющейся величины играет механическая энергия элемента жидкости. = const; (разумеется, для газов такое предположение несправедливо). При таком приближении речь может идти только о рассмотрении поступательного движения элемента жидкости во внешних потенциальных полях сил. К их числу относятся как объёмные силы, в частности, гравитационные, действующие на каждую частицу жидкости, так и упругие силы, вызываемые давлением на элемент жидкости в целом со стороны стенок сосуда. В этом предельном случае роль сохраняющейся величины играет механическая энергия элемента жидкости.Выделим в стационарно текущей идеальной жидкости трубку тока (рис. 4.7.). Рассмотрим объём жидкости, ограниченный стенками трубки тока (реальной трубы). Будем считать, линии тока перпендикулярны сечениям трубки тока S1 и S2. За малое время Dt сквозь сечение S1 пройдёт эле
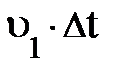 ; каждый объём прошедшей через S1 жидкости массой m = r× DV1 несёт кинетическую энергию ; каждый объём прошедшей через S1 жидкости массой m = r× DV1 несёт кинетическую энергию 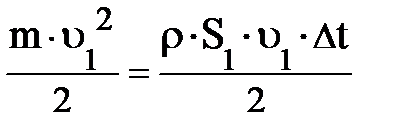 и потенциальную энергию m× g× h1 (рис. 4.7.). Внешняя сила и потенциальную энергию m× g× h1 (рис. 4.7.). Внешняя сила 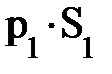 , действующая в сечении S1, смещает указанный объём жидкости DV1 на расстояние , действующая в сечении S1, смещает указанный объём жидкости DV1 на расстояние 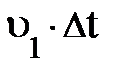 и поэтому совершает положительную работу, равную и поэтому совершает положительную работу, равную 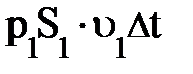 (рис. 4.7.). (рис. 4.7.).
В приближении идеальной и несжимаемой жидкости, и приняв во внимание уравнение неразрывности потока, нетрудно понять, через сечение S2 за то же самое время должен выйти тот же объём жидкости DV1; т.е. DV1 = DV2 = S2× DW = ( В соответствии с законом сохранения энергии изменение энергии, представленное уравнением (1), равно работе DА внешних сил (давления) по перемещению массы жидкости m = r DА = Приравняв правые части уравнений (1) и (2), читатель может самостоятельно получить уравнение Бернулли. Действительно, если учесть уравнение неразрывности потока, m = r× DV1 = r× DV2, а отсюда следует
Следовательно, в установившемся потоке идеальной жидкости полное давление, слагающееся из динамического, гидравлического и статического давлений, постоянно на любом поперечном сечении потока. Уравнение (3) применимо и для газа. Это допустимо, если, например, воздух движется со скоростью не превышающей ~ 200 м/с; вязкостью и сжимаемостью газа при таком движении ещё можно пренебречь. Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 681; Нарушение авторского права страницы