
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Давление под искривлённой поверхностью жидкости.
Капиллярные явления В параграфе 4.1., рис. 4.2. мы выяснили (посмотрели? ), в приповерхностном слое жидкости на молекулу действует равнодействующая сил
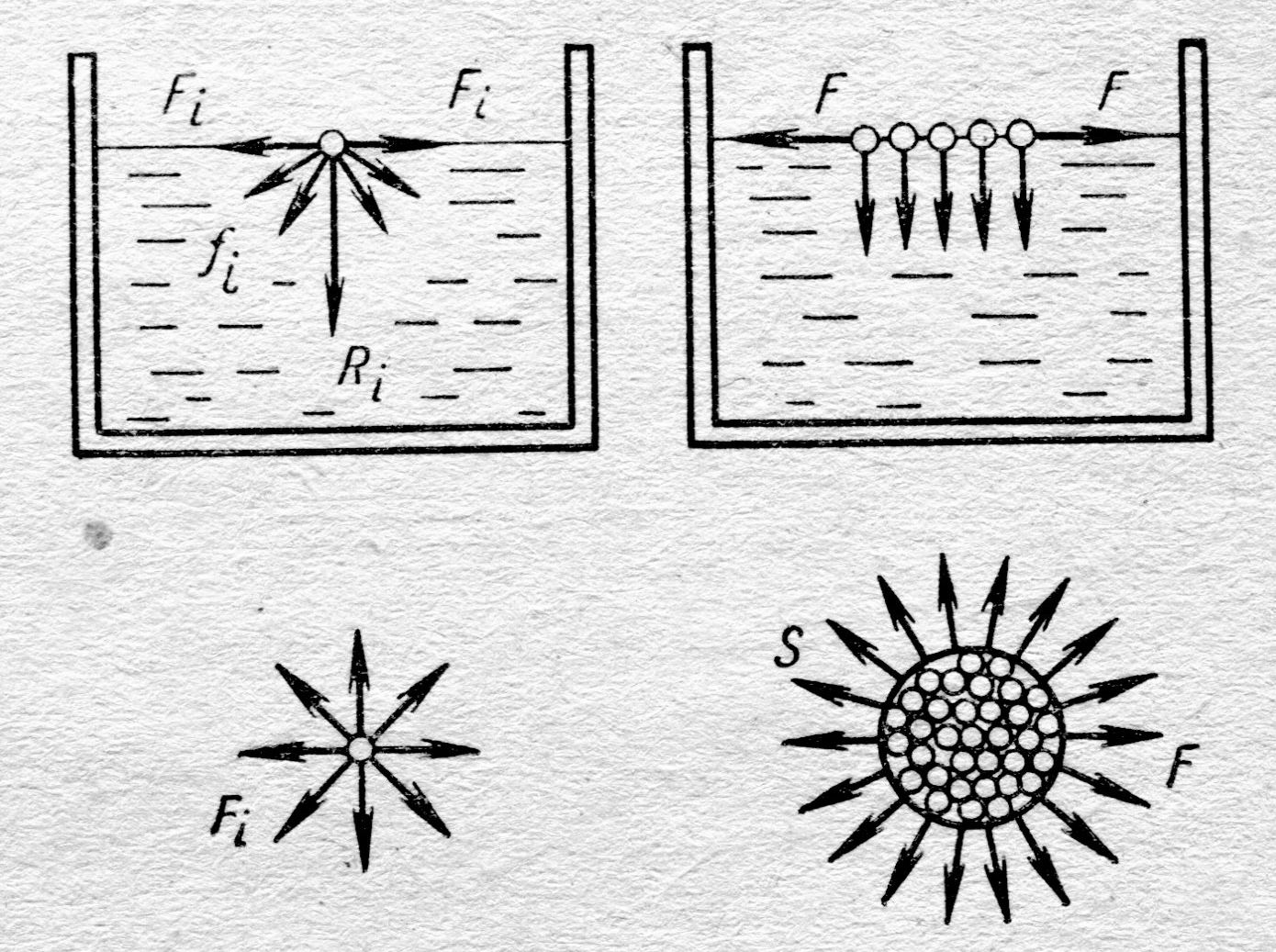 Кроме того, на молекулы поверхностного слоя действуют силы Кроме того, на молекулы поверхностного слоя действуют силы 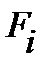 , лежащие в плоскости, касательной к поверхности жидкости (см. рис. 4.8., справа). Эти внешние силы F, растягивающие плёнку, и называют силами поверхностного натяжения. Если выделить на поверхности жидкости площадку S, рис. 4.8., справа (внизу), то силы F, направленные наружу, являются внешними силами; они перпендикулярны периметру площадки S и касательные к поверхности жидкости. Для всех молекул, лежащих внутри площадки S, все эти силы , лежащие в плоскости, касательной к поверхности жидкости (см. рис. 4.8., справа). Эти внешние силы F, растягивающие плёнку, и называют силами поверхностного натяжения. Если выделить на поверхности жидкости площадку S, рис. 4.8., справа (внизу), то силы F, направленные наружу, являются внешними силами; они перпендикулярны периметру площадки S и касательные к поверхности жидкости. Для всех молекул, лежащих внутри площадки S, все эти силы 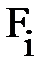 взаимно уравновешиваются. взаимно уравновешиваются.
Всё сказанное об особых условиях, в которых находятся молекулы поверхностного слоя жидкости, в целом относится и к твёрдым телам. Следовательно, твёрдые тела, как и жидкости, обладают поверхностным натяжением. Следует ожидать, если жидкость имеет границу с твёрдым телом, то эта система, с учётом сил межмолекулярного взаимодействия, принимает конфигурацию, соответствующую минимуму суммарной потенциальной энергии; поверхностной, с учётом и поля сил тяжести. В частности, это проявляется на искривлении поверхности жидкости; явление смачивания (не смачивания, например, ртуть). Под искривлённой поверхностью жидкости помимо внутреннего давления силы поверхностного натяжения создают дополнительное давление на жидкость. Оно прибавляется к давлению, созданному поверхностным слоем, или вычитается из него. Кстати, давление, создаваемое поверхностным слоем воды ~ 1, 7× 109 Па, что значительно превышает давление атмосферы; поэтому все жидкости уже сильно сжаты внутренними молекулярными силами. Чтобы вызвать дополнительное уменьшение их объёма, сжать, требуется приложить очень большое внешнее давление. (Вспомните неудачные прыжки в воду в детские годы; «нежная» при умывании вода, больно жалит при взаимодействии с нею за малый промежуток времени.)
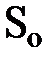 ; радиус основания ; радиус основания  (см. рис. 4.9.). Силы поверхностного натяжения (см. рис. 4.9.). Силы поверхностного натяжения 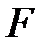 , действующие по периметру площадки S (рис. 4.9.), создают равнодействующую , действующие по периметру площадки S (рис. 4.9.), создают равнодействующую 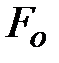 , перпендикулярную основанию , перпендикулярную основанию 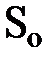 и равную и равную  . Составляющие . Составляющие 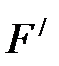 силы поверхностного натяжения силы поверхностного натяжения 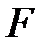 в сумме дают нуль (почему? Нарисуйте вид сверху, поможет). Учитывая, что давление равно силе приходящейся на единицу площади, т.е., в сумме дают нуль (почему? Нарисуйте вид сверху, поможет). Учитывая, что давление равно силе приходящейся на единицу площади, т.е., 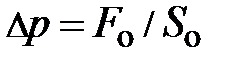 , для дополнительного давления на жидкость от сил поверхностного натяжения, обусловленного кривизной поверхности, получим аналитическое выражение , для дополнительного давления на жидкость от сил поверхностного натяжения, обусловленного кривизной поверхности, получим аналитическое выражение 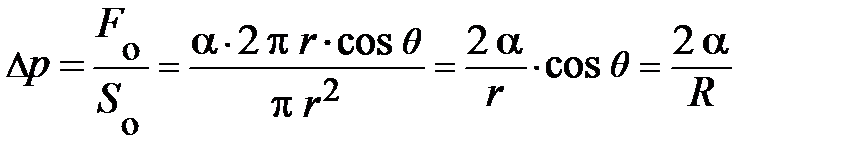 . .
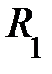 и максимальный и максимальный  ; они лежат во взаимно перпендикулярных плоскостях и называются главными радиусами кривизны поверхности S в данной её точке (рис. 4.10.). Точное выражение для дополнительного давления под искривлённой поверхностью жидкости любой формы вывел французский математик и физик Лаплас в 1805 году. Оно может быть представлено в виде ; они лежат во взаимно перпендикулярных плоскостях и называются главными радиусами кривизны поверхности S в данной её точке (рис. 4.10.). Точное выражение для дополнительного давления под искривлённой поверхностью жидкости любой формы вывел французский математик и физик Лаплас в 1805 году. Оно может быть представлено в виде  . Знак плюс соответствует выпуклой поверхности, знак минус – вогнутой поверхности; . Знак плюс соответствует выпуклой поверхности, знак минус – вогнутой поверхности; 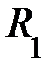 и и  здесь алгебраические величины – если центр кривизны находится под данной поверхностью, радиус кривизны положительный; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен (отобразите на рис; сделали? ). здесь алгебраические величины – если центр кривизны находится под данной поверхностью, радиус кривизны положительный; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен (отобразите на рис; сделали? ).
Если силы сцепления между молекулами жидкости больше, чем между молекулами жидкости и твёрдого тела, то жидкость, искривляясь, стремится уменьшить границу соприкосновения с твёрдым телом, т.е. сжимается, «опускается» по стенкам (рис. 4.11., справа); в этом и состоит суть явления несмачивания. Изогнутую поверхность принято называть мениском, а узкую трубку (щель и т.п.) – капилляром. При большой кривизне мениска внутреннее давление жидкости в капилляре (на уровне горизонта поверхности) будет меньше, чем вне капилляра, на величину избыточного давления под искривлённой (сферической) поверхностью. По закону Паскаля это должно сопровождаться выдавливанием вверх жидкости в капилляре (при смачивании, рис. 4.11., слева). Жидкость в капилляре поднимается до тех пор, пока давление столба жидкости не скомпенсирует уменьшение давления, обусловленное искривлением поверхности жидкости; давление столба жидкости должно равняться капиллярному давлению. Аналитически это запишется Dр = Завершая экскурс в раздел «Элементы механики сплошных сред: жидкости и газы», перечислим его ключевые понятия: квазикристаллическая структура, сфера молекулярного действия, молекулярное давление, макроскопический элемент, гидростатическое давление (объёмные силы), уравнение неразрывности потока, трубка тока, идеальная несжимаемая жидкость, искривлённая поверхность, капиллярное (лапласовское) давление.
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 937; Нарушение авторского права страницы