Распределение энергии по степеням свободы.
Закон парциальных давлений.
Несмотря на простоту вывода основного уравнения молекулярно-кинетической теории газов, формулу 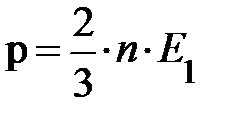 не так-то просто проверить на опыте. Да, мы умеем измерять на опыте давление газа, но у нас нет приборов для прямого измерения величины энергии Е = Е1× n. Человечество вообще не умеет измерять внутреннюю энергию газа в состоянии теплового равновесия. Чтобы реально использовать уравнение кинетической теории газов, приходится прибегать к процедуре косвенных измерений величины Е (энергии). Для этого человечество ввело величину, характеризующую состояние теплового равновесия для любых объектов. Читатель правильно догадался, такой величиной является температура; символ – Т.
не так-то просто проверить на опыте. Да, мы умеем измерять на опыте давление газа, но у нас нет приборов для прямого измерения величины энергии Е = Е1× n. Человечество вообще не умеет измерять внутреннюю энергию газа в состоянии теплового равновесия. Чтобы реально использовать уравнение кинетической теории газов, приходится прибегать к процедуре косвенных измерений величины Е (энергии). Для этого человечество ввело величину, характеризующую состояние теплового равновесия для любых объектов. Читатель правильно догадался, такой величиной является температура; символ – Т.
Пока будем обходиться понятием эмпирической температуры, т.е. той физической величины, которая измеряется на опыте и связана с интуитивным представлением о тепловом равновесии. Эмпирическая температура объекта – это то, что измеряется другим объектом-термометром, приведённым в состояние теплового равновесия с исходным объектом, и служит характеристикой равновесного состояния. В роли такого объекта-термометра может служить любой объект в состоянии теплового равновесия, характеристики которого реагируют на изменение этого состояния.
Из кинетической теории идеального газа следует, давление пропорционально кинетической энергии молекулы (частицы), если объём V, масса газа m и его сортность m неизменны. Вместе с тем из экспериментальных законов Бойля–Мариотта и Гей-Люссака Клапейрону удалось получить уравнение, связывающее все три термодинамических макропараметра вместе; произведение давления и объёма делённое на температуру остаётся постоянным для любого состояния идеального газа 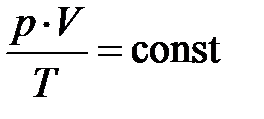 , если сорность и масса газа не изменяются. Эту формулу русский учёный Д.И. Менделееву в 1875 году обобщил для любой массы газа в виде
, если сорность и масса газа не изменяются. Эту формулу русский учёный Д.И. Менделееву в 1875 году обобщил для любой массы газа в виде 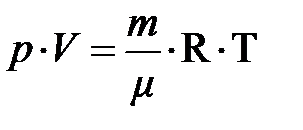 , –– объединённый газовый закон. Отсюда следует, при постоянном объёме и массы газа давление пропорционально температуре. Естественно ожидать, температура системы должна быть пропорциональна энергии частицы. Чтобы найти коэффициент пропорциональности между абсолютной температурой Т и энергией частицы Е1, сопоставим обобщённое уравнение идеального газа и основное уравнение кинетической теории:
, –– объединённый газовый закон. Отсюда следует, при постоянном объёме и массы газа давление пропорционально температуре. Естественно ожидать, температура системы должна быть пропорциональна энергии частицы. Чтобы найти коэффициент пропорциональности между абсолютной температурой Т и энергией частицы Е1, сопоставим обобщённое уравнение идеального газа и основное уравнение кинетической теории:
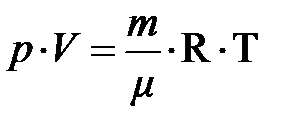
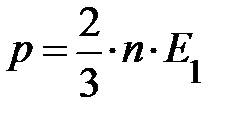 .
.
Если читатель примет к сведению, что m = 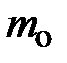 × N,
× N, 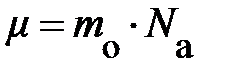 , а
, а 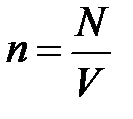 и, проявив терпение, проведёт преобразования первого уравнения, то испытает чувство глубокого удовлетворения, поскольку в результате его действий первое уравнение примет вид
и, проявив терпение, проведёт преобразования первого уравнения, то испытает чувство глубокого удовлетворения, поскольку в результате его действий первое уравнение примет вид 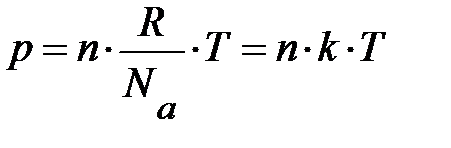 . После преобразований левые части уравнений системы равны, должны быть равны и правые. Отсюда немедленно следует, энергия одной молекулы
. После преобразований левые части уравнений системы равны, должны быть равны и правые. Отсюда немедленно следует, энергия одной молекулы 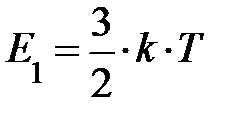 оказывается зависящей лишь от температуры, но не зависит от массы молекулы; буква k, равная
оказывается зависящей лишь от температуры, но не зависит от массы молекулы; буква k, равная 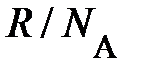 =
= 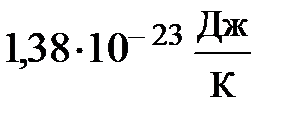 , называется постоянной Больцмана. Здесь весьма важно обратить внимание на формулу
, называется постоянной Больцмана. Здесь весьма важно обратить внимание на формулу 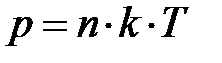 . Если имеется смесь из нескольких сортов газов, результирующее давление может быть записано
. Если имеется смесь из нескольких сортов газов, результирующее давление может быть записано 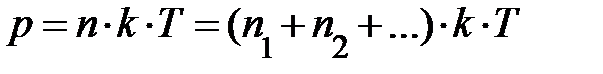 ; здесь
; здесь 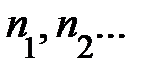 – концентрация различных сортов газов. Выражение перепишем
– концентрация различных сортов газов. Выражение перепишем 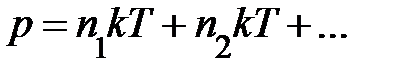 , отсюда немедленно следует закон Дальтона – давление смеси идеальных газов равно сумме парциальных давлений газов, образующих смесь.
, отсюда немедленно следует закон Дальтона – давление смеси идеальных газов равно сумме парциальных давлений газов, образующих смесь.
Следует вернуться к выражению средней энергии молекулы 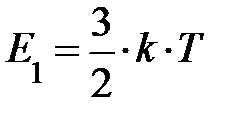 . При выводе его мы учитывали лишь поступательное движение молекул; здесь «тройка» отражает размерность пространства, в котором происходят рассматриваемые события. Следовательно, на одну степень свободы (возможного направления движения) приходится энергия, равная
. При выводе его мы учитывали лишь поступательное движение молекул; здесь «тройка» отражает размерность пространства, в котором происходят рассматриваемые события. Следовательно, на одну степень свободы (возможного направления движения) приходится энергия, равная 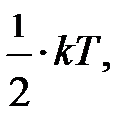 поскольку ни одно из направлений поступательного движения не имеет преимущества. Однако в природе наряду с поступательным движением возможны вращение молекул и колебания атомов в молекуле, входящих в состав молекул. Эти виды движений, также как и поступательное движение, связаны с некоторым запасом энергии, определить который позволяет устанавливаемое статистической физикой положение о равнораспределении энергии по степеням свободы молекул. Если предположить, что ни один из видов движения не имеет преимущества перед другими, то на любую степень свободы поступательного, вращательного и колебательного движений должна приходиться в среднем одинаковая энергия, равная
поскольку ни одно из направлений поступательного движения не имеет преимущества. Однако в природе наряду с поступательным движением возможны вращение молекул и колебания атомов в молекуле, входящих в состав молекул. Эти виды движений, также как и поступательное движение, связаны с некоторым запасом энергии, определить который позволяет устанавливаемое статистической физикой положение о равнораспределении энергии по степеням свободы молекул. Если предположить, что ни один из видов движения не имеет преимущества перед другими, то на любую степень свободы поступательного, вращательного и колебательного движений должна приходиться в среднем одинаковая энергия, равная 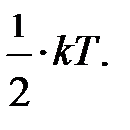 В этом и состоит суть положения о равнораспределении энергии по степеням свободы. Из этого предположения следует, чем сложнее молекула, тем больше число её степеней свободы, тем больше среднее значение энергии одной молекулы
В этом и состоит суть положения о равнораспределении энергии по степеням свободы. Из этого предположения следует, чем сложнее молекула, тем больше число её степеней свободы, тем больше среднее значение энергии одной молекулы 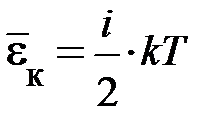 ; здесь
; здесь 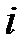 – сумма поступательных, вращательных и колебательных степеней свободы
– сумма поступательных, вращательных и колебательных степеней свободы 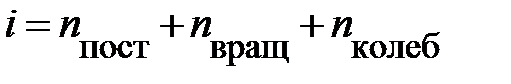 . Из школьного курса известно, молекула кислорода, азота состоит из двух атомов, соответственно,
. Из школьного курса известно, молекула кислорода, азота состоит из двух атомов, соответственно, 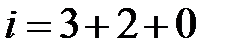 .
.
Барометрическая формула
До сих пор мы рассматривали идеальный газ в состоянии теплового равновесия как совокупность реальных частиц испытывающих столкновения и подчиняющихся законам динамики системы частиц. Перейдём к учёту воздействий на идеальный газ внешних полей. Будем рассматривать их в одночастичном приближении. В этом приближении идеальный газ может быть представлен совокупностью свободных «квазичастиц» индивидуального типа, каждая из которых движется независимо с эффективной скоростью, вообще не участвуя в каких-либо столкновениях. При таком подходе включение внешнего поля сопровождается движением каждой из квазичастиц в этом поле. Задача состоит в том, чтобы выяснить, как воздействие внешних полей сказывается на характеристиках газа в целом.
Поскольку взаимодействие в газах не является сильным и можно воспользоваться одночастичным приближением, дополним его приближением «среднего поля». Согласно этому приближению взаимодействие частиц можно учесть, перейдя от совокупности взаимодействующих «квазичастиц» к совокупности независимых «квазичастиц», движущихся в некоем внешнем «среднем поле». Учёт такого взаимодействия также оказывает воздействие на свойства газа в целом.
Итак, мы помещаем газ в потенциальное внешнее поле. Для простоты пусть это будет поле тяготения вблизи поверхности Земли. Его можно считать однородным. Действительно, по закону тяготения Ньютона тела притягиваются к Земле с силой 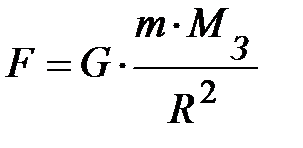 . Здесь G – постоянная всемирного тяготения, равная 6, 67× 10–11 (Н× м2) / кг2; R и МЗ – соответственно, радиус и масса Земли; m – масса элемента газа. На высоте h от поверхности Земли выражение силы принимает вид:
. Здесь G – постоянная всемирного тяготения, равная 6, 67× 10–11 (Н× м2) / кг2; R и МЗ – соответственно, радиус и масса Земли; m – масса элемента газа. На высоте h от поверхности Земли выражение силы принимает вид: 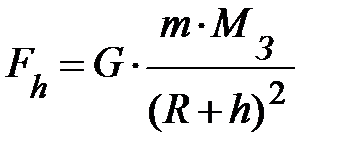 . Найдём разность силы тяжести на поверхности Земли и на высоте h от поверхности Земли, т.е.
. Найдём разность силы тяжести на поверхности Земли и на высоте h от поверхности Земли, т.е. 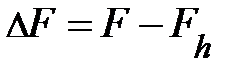 . Набравшись терпения и проведя преобразования, читатель получит аналитическое выражение вида:
. Набравшись терпения и проведя преобразования, читатель получит аналитическое выражение вида: 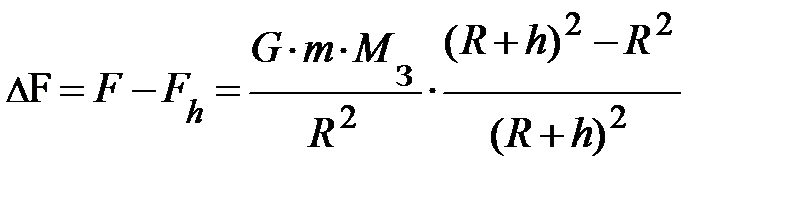 . Возводя в квадрат в числителе второго множителя, и проведя ещё раз преобразования, получим выражение вида;
. Возводя в квадрат в числителе второго множителя, и проведя ещё раз преобразования, получим выражение вида; 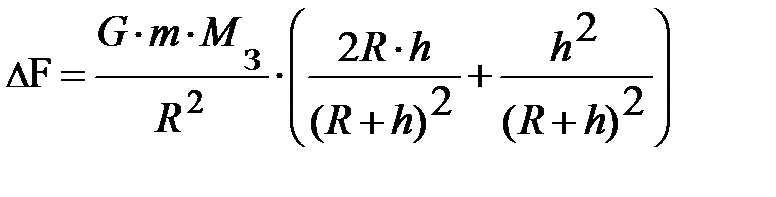 . Проанализируем выражение в скобках. Если учтём, что атмосферный слой простирается до 25÷ 30 км, а радиус Земли R порядка 6400 км, немедленно получаем – второе слагаемое в скобках ~ 2× 10–5. Читатель может самостоятельно убедиться в том, что первое слагаемое в скобках не превышает 1× 10–2. Таким образом, разность силы тяжести на высоте 30 км составляет порядка одной сотой от силы тяжести на поверхности Земли. Если высота h составляет десятки или сотни метров, то разность силы тяжести будет ещё меньше, что даёт основания считать поле тяготения вблизи поверхности Земли однородным. Однако теперь закон Паскаля о постоянстве давления для выделенного элементарного объёма газа DV, помещённого в потенциальное внешнее поле Земли, справедлив только в направлениях, где поле Земли отсутствует (рис. 5.2.).
. Проанализируем выражение в скобках. Если учтём, что атмосферный слой простирается до 25÷ 30 км, а радиус Земли R порядка 6400 км, немедленно получаем – второе слагаемое в скобках ~ 2× 10–5. Читатель может самостоятельно убедиться в том, что первое слагаемое в скобках не превышает 1× 10–2. Таким образом, разность силы тяжести на высоте 30 км составляет порядка одной сотой от силы тяжести на поверхности Земли. Если высота h составляет десятки или сотни метров, то разность силы тяжести будет ещё меньше, что даёт основания считать поле тяготения вблизи поверхности Земли однородным. Однако теперь закон Паскаля о постоянстве давления для выделенного элементарного объёма газа DV, помещённого в потенциальное внешнее поле Земли, справедлив только в направлениях, где поле Земли отсутствует (рис. 5.2.).
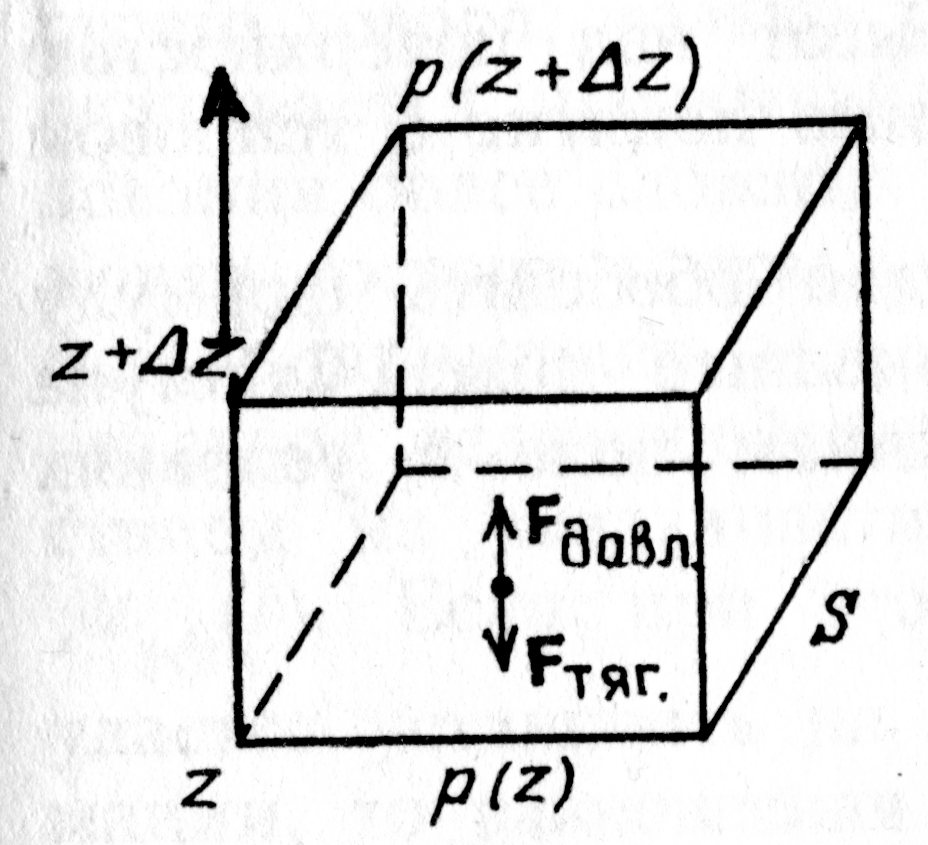
Действительно, на каждую частицу выделенного объёма газа D
V в направлении оси
Z теперь действует сила тяготения
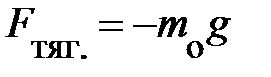
, направленная в противоположную оси
Z сторону (см. рис. 5.2.); здесь
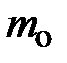
– масса частицы. Учитывая, что на элемент объёма газа D
V действует сила
m×
g = –
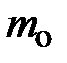
×
n× D
V×
g, где
m – масса объёма газа D
V, выраженная через концентрацию частиц
n и объём выделенного элемента газа
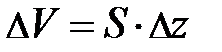
,
условие равновесия сил, действующих на элемент D
V объёма газа в направлении оси
Z, примет вид: –
mо×
n× D
V×
g =
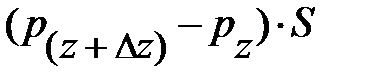
, здесь
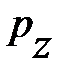
– давление окружающего газа на нижний уровень
S выделенного объёма газа D
V (см. рис. 5.2.);
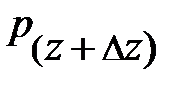
– давление окружающего газа на верхний уровень выделенного объёма D
V;
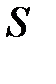
– площадь основания элемента D
V объёма; знак «–» обусловлен тем, что направление силы тяготения
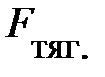
противоположно направлению оси
Z (см. рис.5.2.), тогда как разность давлений окружающего газа на верхнюю и нижнюю грани объёма D
V создаёт силу давления
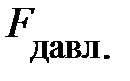
, направленную в положительном направлении оси
Z, т.е. вверх.
Почему сила давления 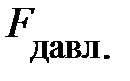 окружающего газа на выделенный элемент объёма DV направлена вверх? На с. 53 показано,
окружающего газа на выделенный элемент объёма DV направлена вверх? На с. 53 показано, 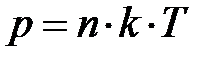 ; отсюда следует, только два параметра определяют давление газа – концентрация молекул газа n и его температура Т. Ранее, на с. 54, показано, температура Т среды определяет энергию поступательного движения молекул газа. Наш жизненный опыт подтверждает, численное значение температуры вблизи поверхности Земли в данном месте относительно постоянно по высоте. Естественно предположить, величина давления р «чувствительна» к концентрации молекул газа n в единице объёма. Если учесть рассуждения данного абзаца, условие равновесия сил на элемент объёма газа DV принимает вид: –mо× n× DV× g =
; отсюда следует, только два параметра определяют давление газа – концентрация молекул газа n и его температура Т. Ранее, на с. 54, показано, температура Т среды определяет энергию поступательного движения молекул газа. Наш жизненный опыт подтверждает, численное значение температуры вблизи поверхности Земли в данном месте относительно постоянно по высоте. Естественно предположить, величина давления р «чувствительна» к концентрации молекул газа n в единице объёма. Если учесть рассуждения данного абзаца, условие равновесия сил на элемент объёма газа DV принимает вид: –mо× n× DV× g = 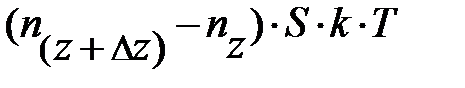 =
= 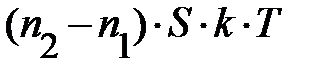 . Так как Dz мало, следует ожидать, разность концентраций частиц по высоте (рис. 5.2.) с координатами z и z+Dz может быть записана
. Так как Dz мало, следует ожидать, разность концентраций частиц по высоте (рис. 5.2.) с координатами z и z+Dz может быть записана 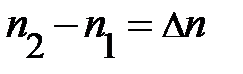 . Аналитическая запись условия равновесия сил принимает конечный вид:
. Аналитическая запись условия равновесия сил принимает конечный вид: 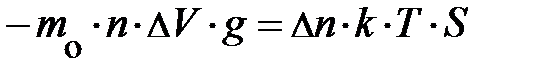 . Читатель, рассуждая, должен пояснить себе, при каком соотношении числовых значений
. Читатель, рассуждая, должен пояснить себе, при каком соотношении числовых значений 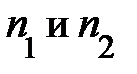 сила давления окружающего газа на выделенный элемент объёма DV совпадает с направлением оси Z (подсказку можно усмотреть на рис.5.2.).
сила давления окружающего газа на выделенный элемент объёма DV совпадает с направлением оси Z (подсказку можно усмотреть на рис.5.2.).
Проанализируем условие равновесия сил на выделенный элемент объёма газа 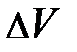 :
: 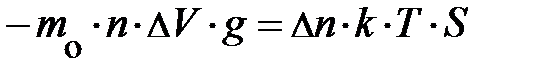 ; здесь
; здесь 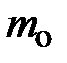 – масса квазичастицы газа; k – постоянная Больцмана, численное значение которой приведено на с. 53; S –площадь выделенного элемента объёма газа
– масса квазичастицы газа; k – постоянная Больцмана, численное значение которой приведено на с. 53; S –площадь выделенного элемента объёма газа 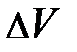 , находящегося во внешнем силовом поле; Т и g, соответственно, характеристики температурного поля среды и внешнего силового поля. Если учесть, что
, находящегося во внешнем силовом поле; Т и g, соответственно, характеристики температурного поля среды и внешнего силового поля. Если учесть, что 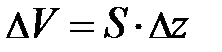 , то после несложных преобразований уравнения равновесия читатель самостоятельно может получить формулу вида:
, то после несложных преобразований уравнения равновесия читатель самостоятельно может получить формулу вида: 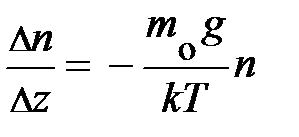 . Из неё следует, скорость изменения концентрации газа с высотой определяется концентрацией частиц в единице объёма n и отношением между силовым и потенциальным полем. Переходя к бесконечно малым величинам
. Из неё следует, скорость изменения концентрации газа с высотой определяется концентрацией частиц в единице объёма n и отношением между силовым и потенциальным полем. Переходя к бесконечно малым величинам 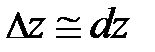 , формула принимает вид:
, формула принимает вид: 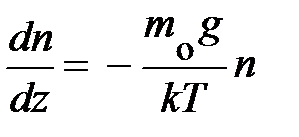 ; получили уравнение в дифференциальной форме. Данное уравнение позволяет найти зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия. Действительно, разделяя переменные
; получили уравнение в дифференциальной форме. Данное уравнение позволяет найти зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия. Действительно, разделяя переменные 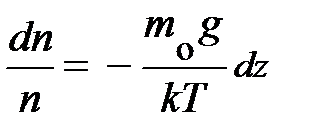 и проводя интегрирование
и проводя интегрирование 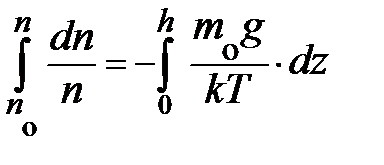 , получаем уравнение вида:
, получаем уравнение вида: 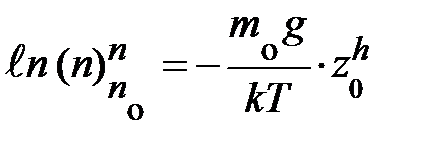 ; здесь n и z
; здесь n и z 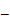 переменные, символы у интегралов сверху и снизу показывают, соответственно, максимальное и минимальное значение, принимаемое переменными. Подставляя эти значения в уравнение, получаем аналитическое выражение вида:
переменные, символы у интегралов сверху и снизу показывают, соответственно, максимальное и минимальное значение, принимаемое переменными. Подставляя эти значения в уравнение, получаем аналитическое выражение вида: 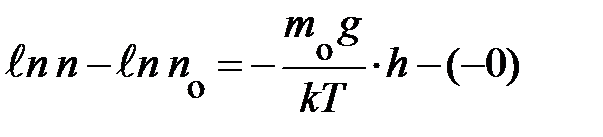 ; если учесть, что разность логарифмов равна логарифму частного, выражение запишется:
; если учесть, что разность логарифмов равна логарифму частного, выражение запишется: 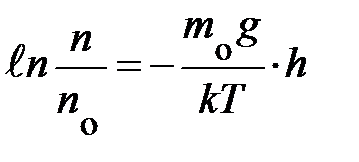 . Наконец, проведя последнюю математическую операцию – потенцирование, получаем формулу, характеризующую зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия:
. Наконец, проведя последнюю математическую операцию – потенцирование, получаем формулу, характеризующую зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия: 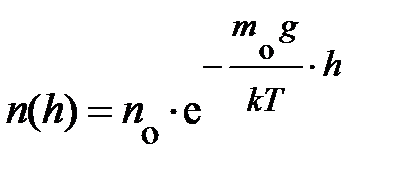 . Из неё следует – «борьба» между внешним потенциальным полем и тепловым определяет распределение частиц в атмосфере; чем меньше потенциальная энергия молекул, тем больше их плотность.
. Из неё следует – «борьба» между внешним потенциальным полем и тепловым определяет распределение частиц в атмосфере; чем меньше потенциальная энергия молекул, тем больше их плотность.
Учитывая, что закон Клапейрона-Менделеева справедлив для любой точки формула распределения концентрации частиц может быть переписана для давления газа в атмосфере у поверхности Земли. Действительно, 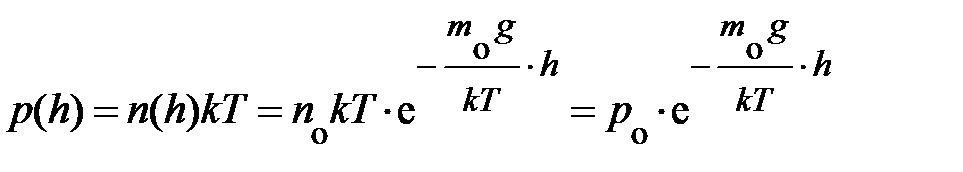 . Полученная формула называется барометрической.
. Полученная формула называется барометрической.
Повторяя те же рассуждения, формула распределения концентрации частиц во внешнем поле может быть обобщена на произвольное потенциальное поле; в дальнейшем нам с этим придётся встретиться. Формулу для концентрации частиц во внешнем поле в условиях теплового равновесия принято называть формулой Больцмана: 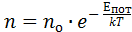 .
.
Завершая экскурс в раздел «Тепловые явления. Термодинамический и статистический методы исследования», перечислим его ключевые понятия: термодинамическая система, макро- и микропараметры системы, состояние системы, «квазичастица» индивидуального типа, идеальный газ, основное уравнение кинетической теории газов; тепловое равновесие, понятие температуры (эмпирической), степень свободы молекулы, равнораспределение энергии по степеням свободы; идеальный газ во внешнем поле, барометрическая формула, распределение Больцмана.
Популярное:


 Действительно, на каждую частицу выделенного объёма газа DV в направлении оси Z теперь действует сила тяготения
Действительно, на каждую частицу выделенного объёма газа DV в направлении оси Z теперь действует сила тяготения 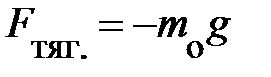 , направленная в противоположную оси Z
, направленная в противоположную оси Z 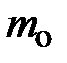 – масса частицы. Учитывая, что на элемент объёма газа DV действует сила m× g = –
– масса частицы. Учитывая, что на элемент объёма газа DV действует сила m× g = – 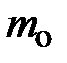 × n× DV× g, где m – масса объёма газа DV, выраженная через концентрацию частиц n и объём выделенного элемента газа
× n× DV× g, где m – масса объёма газа DV, выраженная через концентрацию частиц n и объём выделенного элемента газа 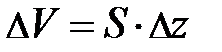 , условие равновесия сил, действующих на элемент DV объёма газа в направлении оси Z, примет вид: –mо× n× DV× g =
, условие равновесия сил, действующих на элемент DV объёма газа в направлении оси Z, примет вид: –mо× n× DV× g = 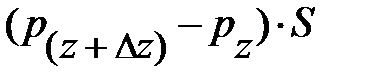 , здесь
, здесь 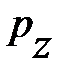 – давление окружающего газа на нижний уровень S выделенного объёма газа DV (см. рис. 5.2.);
– давление окружающего газа на нижний уровень S выделенного объёма газа DV (см. рис. 5.2.); 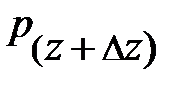 – давление окружающего газа на верхний уровень выделенного объёма DV;
– давление окружающего газа на верхний уровень выделенного объёма DV; 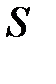 – площадь основания элемента DV объёма; знак «–» обусловлен тем, что направление силы тяготения
– площадь основания элемента DV объёма; знак «–» обусловлен тем, что направление силы тяготения 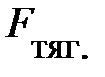 противоположно направлению оси Z (см. рис.5.2.), тогда как разность давлений окружающего газа на верхнюю и нижнюю грани объёма DV создаёт силу давления
противоположно направлению оси Z (см. рис.5.2.), тогда как разность давлений окружающего газа на верхнюю и нижнюю грани объёма DV создаёт силу давления 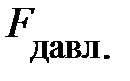 , направленную в положительном направлении оси Z, т.е. вверх.
, направленную в положительном направлении оси Z, т.е. вверх.