
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Изопроцессы в идеальном газе; теплоёмкость газов
Переходя к рассмотрению простейших газовых процессов, учтём, реальный процесс есть последовательность равновесных состояний, что позволяет отобразить его соответствующей линией в системе координат, по осям которой отложены параметры состояния системы V, P. Выбор системы координат обусловлен тем, что площадь, ограниченная линией процесса и двумя крайними координатами начального и конечного значений объёма, равна работе сжатия или расширения газа. При рассмотрении закономерностей ограничимся газами, удовлетворяющими уравнению газового состояния, уравнению Менделеева-Клапейрона. Зная уравнение состояния вещества, с помощью первого начала термодинамики можно получить ряд полезных следствий о поведении системы в различных условиях. Изохорический процесс, объём газа в течение всего процесса сохраняется постоянным: а) уравнение процесса V
т.е. из (4) следует, при изохорическом процессе давление газа прямо пропорционально абсолютной температуре. На графике в системе координат V, P это отобразится так, как представлено на рис. 7.1.; б) изменение внутренней энергии газа можно рассчитать по формуле, установленной в параграфе 7.1.:
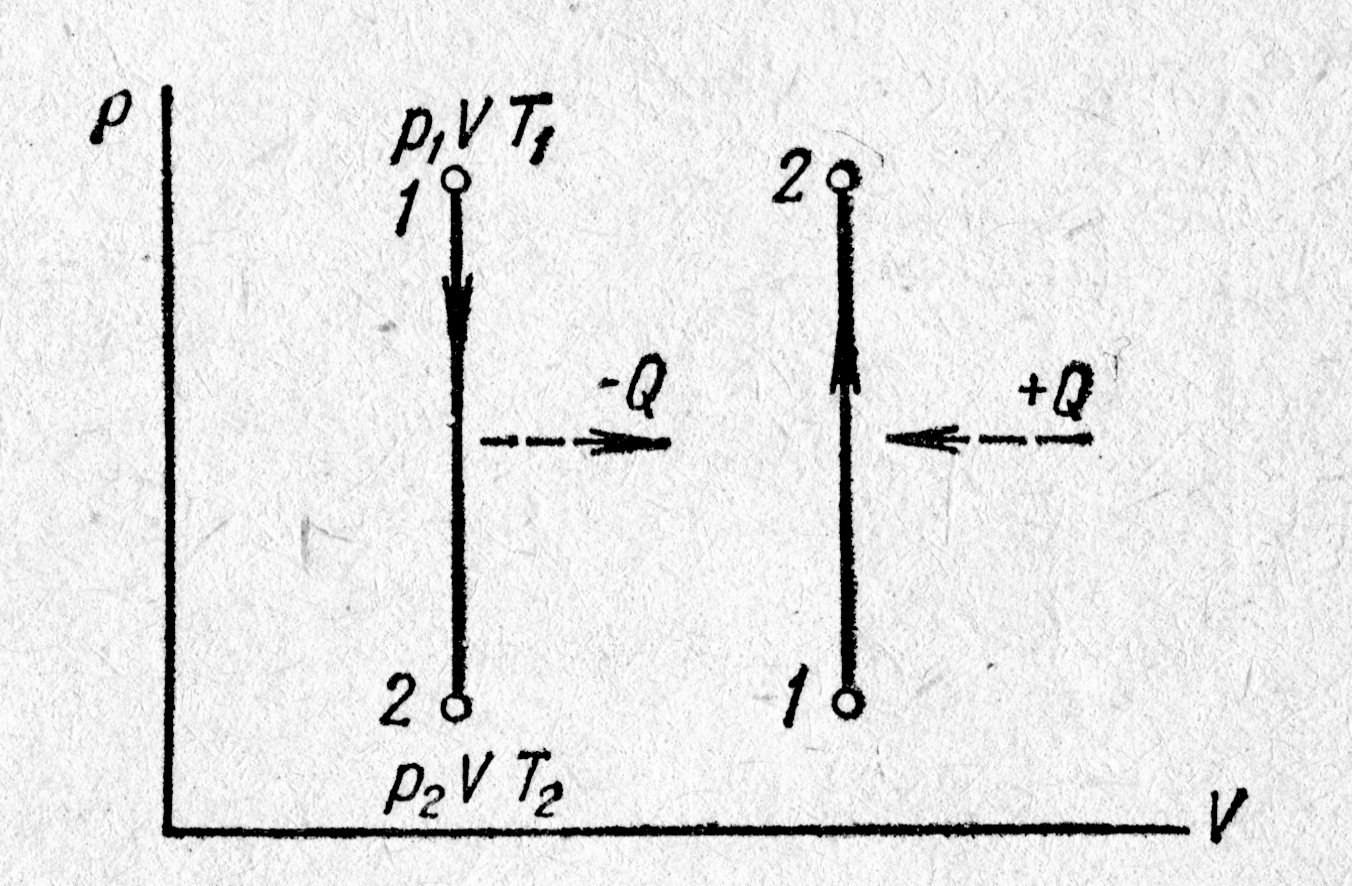 Если система получает тепло, это соответствует графику 1-2 на рис. 7.1.; получение теплоты отображено на графике стрелкой, а теплота отображена со знаком +Q. Если система отдаёт теплоту среде, это соответствует графику 2-1; внутренняя энергия системы уменьшается прямо пропорционально температуре. Если система получает тепло, это соответствует графику 1-2 на рис. 7.1.; получение теплоты отображено на графике стрелкой, а теплота отображена со знаком +Q. Если система отдаёт теплоту среде, это соответствует графику 2-1; внутренняя энергия системы уменьшается прямо пропорционально температуре. в) внешняя работа системы равна нулю; действительно, поскольку V = const, то г) теплообмен системы с окружающей средой, согласно первому началу термодинамики, запишется Q = U2 – U1 + A, поскольку A = 0, то количество тепла Q, полученное или отданное системой, запишется,
здесь сv удельная теплоёмкость газа в данном процессе, которая, как показано в параграфе 7.1., связана с молярной теплоёмкостью соотношением Из уравнения (6) следует ещё одно важное следствие; если читатель проведёт преобразования, в частности, сократит разность температур Преобразования самостоятельно провели? Изобарический процесс, давление газа в течение всего процесса поддерживается постоянным (рис. 7.2.): а) уравнение процесса р
б) изменение внутренней энергии газа рассчитывается по формуле, установленной в параграфе 7.1.: в) внешняя работа, как следует из графика, рис. 7.2, не равна нулю. Система обменивается со средой не только теплом, но и работой без изменения давления в системе. Наиболее распространённый вариант этого процесса состоит в том, что система получает из среды тепло, но не обращает его целиком на увеличение своей внутренней энергии, а частично возвращает в среду уже в виде механической работы. Поскольку для изобарического процесса р
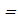 const, теплота Q, подводимая к системе, аналитически может быть представлена формулой: const, теплота Q, подводимая к системе, аналитически может быть представлена формулой: 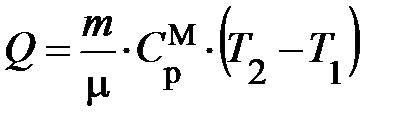 . Подставляя в первое начало аналитические выражения подводимой теплоты Q, изменения внутренней энергии U2 – U1, внешней работы A получим уравнение вида: . Подставляя в первое начало аналитические выражения подводимой теплоты Q, изменения внутренней энергии U2 – U1, внешней работы A получим уравнение вида:
В уравнении (8) сокращаются однородные члены: разность температур
Полученное соотношение между теплоёмкостями при постоянном давлении и постоянном объёме называется уравнением Майера. Соотношение Майера через число степеней свободы примет вид:
Изотермический процесс, температура термодинамической системы в течение всего процесса поддерживается постоянной: а) уравнение процесса T
Разделив первое уравнение на второе, получим – произведение давления на объём первого состояния равно произведению давления на объём конечного состояния: б) изменение внутренней энергии системы равно нулю; действительно, поскольку DU = в) внешняя работа, равная площади фигуры 1-2-3-4-1, рис. 7.3., может быть рассчитана по формуле
На графике, рис. 7.3., это соответствует площади фигуры 1-2-3-4-1. Здесь уместно высказать пожелание. При необходимости в уравнении (12) выражение г) теплообмен между газом и внешней средой при изотермическом процессе не может быть найден по формулам, аналогичным (6) или (8), так как T
Если из уравнения состояния выразить давление р(V), уравнение (13) примет вид: Итак, из уравнения теплообмена (13) следует, при изотермическом процессе, совершаемом идеальным газом, теплообмен между термодинамической системой и окружающей средой по величине и знаку равен внешней работе. При расширении, нижняя кривая рис. 7.3., логарифм отношения Практическое осуществление изотермического процесса затруднительно. Для того, чтобы процесс был хотя бы приближённо изотермическим, необходимо стенки сосуда, через которые термодинамическая система общается со средой, сделать идеально теплопроводящими и вести процесс медленно, чтобы тепло (или работа) успевало возвращаться среде в виде работы (или тепла) не задерживаясь в системе.
Адиабатический процесс Уравнения изопроцессов, при которых один из основных параметров состояния системы не изменяется, читателю знакомы из школьного курса физики: изохорический (V); изобарический (P); изотермический (Т). Эти уравнения добыты человечеством путём экспериментальных исследований. Вместе с тем уравнение адиабаты, связывающее параметры идеального газа при адиабатическом процессе, получить таким путём исследований не представляется возможным, если не принимать во внимание – процесс идёт без теплообмена с окружающей средой. Это возможно, если обеспечена идеальная теплоизоляция и быстрое проведение процесса, чтобы тепло не успело перейти из системы в среду или обратно. Предпримем усилия для строгого обоснования уравнения адиабаты. Адиабатическим называют процесс, при котором теплообмен термодинамической системы с окружающей средой отсутствует на протяжении всего процесса Переходя к нахождению уравнения, связывающего параметры идеального газа при адиабатическом процессе, учтём, что элементарная работа
Полученные выражения для элементарной работы
Преобразуем его следующим образом: сократим на постоянный множитель
Наконец, разделив переменные и приняв во внимание выражение (9), откуда следует
Внимательный читатель, приняв во внимание формулу (9) и проведя преобразования, убедился, что постоянная
Интегрируя уравнение (14) в пределах от
приходим к уравнению,
Учтём, разность логарифмов равна логарифму частного, в результате получаем уравнение вида:
Если учесть свойства логарифмов, в частности, множитель перед логарифмом является показателем степени для выражения под логарифмом, уравнение запишется:
Логарифмы в уравнении (15) равны, если равны выражения под логарифмами, отсюда немедленно следует:
окончательно уравнение адиабатического процесса принимает вид:
Пытливый читатель, воспользовавшись уравнением состояния, может выразить из него температуру и, подставив в уравнение (17), получить уравнение адиабатического процесса, связывающего давление и объём:
Формулы (17) и (18), связывающие параметры идеального газа при равновесном адиабатическом процессе, называются уравнениями Пуассона. Отношение Ср/Сv = g называется показателем адиабатического процесса; учитывая «чувствительность» молярных теплоёмкостей идеального газа к числу степеней свободы частиц, показатель адиабаты может быть представлен в виде:
Для практического осуществления процессов, близких к адиабатическим, возможны два пути: 1) очень быстрое изменение объёма газа; и 2) изменение объёма очень большой массы газа. В обоих случаях не успевает произойти значительного теплообмена между системой (газом) и окружающей средой, что равносильно наличию хорошей теплоизоляции между ними.
Круговые процессы
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 586; Нарушение авторского права страницы