
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Пересечение прямой линии и плоскости
Если одна из пересекающихся фигур занимает частное положение, то точка пересечения находится значительно проще. 7.2.1. Задание: найти точку пересечения отрезка прямой АВ с проецирующей плоскостью Р (рис. 7.2).
Рис. 7.2 Решение: проанализировав чертеж, легко заметить, что плоскость Р занимает проецирующее положение (плоскость Р перпендикулярна к плоскости П2. ) В первую очередь определяем фронтальную проекцию С2 точки пересечения отрезка прямой АВ с плоскостью Р. Горизонтальная проекция С1 искомой точки находится с помощью линии связи на горизонтальной проекции отрезка прямой АВ . На плоскость П2 плоскость Р проецируется в линию, совпадающую с фронтальным следом Р2 , следовательно прямая видима по обе стороны от следа Р2. При определении видимости горизонтальной проекции прямой необходимо установить, какой участок прямой находится над плоскостью Р, т.е. будет видимым на горизонтальной проекции. Таким участком является часть проекции отрезка, расположенная левее проекции С1. 7.2.2. Задание: найти точку пересечения проецирующей прямой т с плоскостью Решение: из чертежа видно, что плоскость, заданная треугольником ABC, занимает общее положение относительно плоскостей проекции, прямая m является горизонтально проецирующей, m
Построение начинается с горизонтальной проекции. В пересечении её фронтальной проекции 12-22 с фронтальной проекцией прямой m находят фронтальную проекцию К2 искомой точки К. 7.2.3. Задание: найти точку пересечения прямой m общего положения с плоскостью общего положения Σ ( ABC ) (рис. 7.4). Решение: в данной задаче прямая m и плоскость Σ занимают общее положение относительно плоскостей проекции. Задача решается по следующей схеме: · прямую m заключают в плоскость · находят линию DE пересечения плоскостей Σ ( АВС ) и · определяют точку К пересечения прямой m с плоскостью Σ в пересечении прямых DE и т.д.
Видимость прямой m относительно плоскости Метод конкурирующих точек заключается в следующем: Для определения видимости прямой m на горизонтальной плоскости выбирается пара точек 1 и D (см.рис.7.4). У этих точек координаты у одинаковы у1=уD, координаты z различны ( zD > z2), точка D выше точки 1 (координата точки D больше координаты точки 1 ). Следовательно, на горизонтальной проекции точка D видима, а 1 невидима.Tак как точка 1 принадлежит прямой m, то левее проекции точка K1 прямая m находится ниже плоскости треугольника ABC, то есть она не видима (должна быть проведена штриховой линией). Для определения видимости на фронтальной проекции можно воспользоваться парой точек 2 и 3 и рассмотреть вопрос видимости аналогично точкам 1 и D. Параллельность прямой и плоскости
Прямая и плоскость параллельны, если в плоскости имеется прямая, параллельная заданной прямой. 7.3.1 Задание: построить проекции прямой, проходящей через точку А и параллельной прямой m, принадлежащей плоскости Σ (BCD) (рис. 7.5).
Рис. 7.5 Решение: в условии задачи задана фронтальная проекция m2 прямой m. Находим горизонтальную проекцию m1 прямой m. Условия параллельности прямой и плоскости: прямая параллельна плоскости, если она параллельна какой-то прямой, расположенной в данной плоскости. Используя это условие, строят проекции искомой прямой, проходящие через точку А; n1 проводятся параллельно m1 , n2 — параллельно m2.
ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ К ПЛОСКОСТИ
Основные положения
Обратимся к рисунку 8.1, на котором изображена плоскость Прямая n перпендикулярна к любой прямой плоскости Если
Угол между прямой n фронталью f плоскости проецируется на фронтальную плоскость проекций прямым углом (его сторона Если Если прямая перпендикулярна к плоскости, то ее проекции перпендикулярны к одноименным проекциям линий уровня этой плоскости. На рисунке 8.2 через точку N проведена прямая m, перпендикулярная к плоскости Σ. Для этого в плоскости Σ (а^b) определены горизонталь h и фронталь f, и горизонтальная проекция перпендикуляра проведена перпендикулярно к горизонтальной проекции горизонтали, а фронтальная проекция — перпендикулярно к фронтальной проекции фронтали: Действительно, из чертежа следует, что прямая m перпендикулярна к прямой h, так как угол между горизонтальными проекциями сторон угла прямой и одна сторона его ( h ) параллельна плоскости П1. Точно так же прямая m перпендикулярна к прямой f. Но если прямая линия перпендикулярна к двум пересекающимся прямым плоскости, то она перпендикулярна к этой плоскости.
Рис. 8.2
В том случае, когда плоскость задана следами (рис. 8.3), проекции перпендикуляра располагаются перпендикулярно к одноименным следам плоскости: Плоскость, перпендикулярную к данной прямой, определяют с помощью пересекающихся линий уровня. На рисунке 8.4 (а- условие, 6 - решение) через точку А проведена плоскость Горизонталь h плоскости проходит через точку А На рисунке 8.4 фронталь f2 проходит через точку В
Рис. 8.3 Рис. 8.4
На рисунке 8.4 фронталь f2 проходит через точку В На рисунке 8.5 показана прямая n перпендикулярная горизонтально проецирующей плоскости. Эта прямая является горизонталью. На рисунке 8.6 изображена прямая n, перпендикулярная к фронтально проецирующей плоскости. Эта прямая n является фронталью. На рисунке 8.7 изображен отрезок прямой ( MN ), перпендикулярный к профильно проецирующей плоскости Это не должно нас удивлять, так как (h≡ f ), а перпендикулярность прямой и плоскости обеспечивается перпендикулярностью этой прямой к двум пересекающимся прямым плоскости. Для решения задачи нужно построить профильный след. Тогдa M3N3 Если требуется определить, перпендикулярна ли некоторая прямая т кзаданной плоскости Σ, то через какую-нибудь точку М этой прямой следует провести перпендикуляр n к плоскости Σ (рис. 8.8). При совпадении линии m и n прямая m перпендикулярна к плоскости Σ.
Рис. 8.5 Рис. 8.6
Рис. 8.7 Рис. 8.8
Примеры решения задач
8.2.1. Задание: Построить перпендикуляр из точки А на плоскость Решение: исходя из принципа перпендикулярности прямой и плоскости (прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости), необходимо в плоскости провести две пересекающиеся прямые: горизонталь h и фронталь f (рис. 8.9).

Рис.8.9
 и и  . Если плоскость задана следами, то . Если плоскость задана следами, то  и и 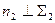 (рис. 8.10). (рис. 8.10).
Основание перпендикуляра определяется как точка пересечения его с плоскостью. Для этого нужно провести через нормаль проецирующую плоскость
Методы ПРЕОБРАЗОВАНИЯ проекций Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 649; Нарушение авторского права страницы