
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Общие понятия системы линейных уравнений.
Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной. Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного. Определение. Для системы линейных уравнений матрица А = А*= Определение. Если b1, b2, …, bm = 0, то система называется однородной. Замечание. Однородная система всегда совместна, т.к. всегда имеет нулевое решение. Элементарные преобразования систем. 1. Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю. 2. Перестановка уравнений местами. 3. Удаление из системы уравнений, являющихся тождествами для всех х.
Формулы Крамера. Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Теорема. Система из n уравнений с n неизвестными
в случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам: xi = Di = Пример. Найти решение системы уравнений: D = D1 = x1 = D2 = x2 = D3 = x3 = Замечание 1. Если система однородна, т.е. bi = 0, то при D¹ 0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0. Замечание 2. При D = 0 система имеет бесконечное множество решений.
Метод обратной матрицы. Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных. Пусть дана система уравнений: A = B = X = Тогда систему уравнений можно записать: A× X = B. Домножим слева обе части равенства на A-1: A-1× A× X = A-1× B, т.к. А-1× А = Е, то Е× Х = А-1× В, то справедлива следующая формула: Х = А-1× В Таким образом, для применения данного метода необходимо находить обратную матрицу. Пример. Решить систему уравнений: Х = Найдем обратную матрицу А-1. D = det A = M11 = M12 = M13 =
A-1 = Cделаем проверку: A× A-1 = Находим матрицу Х. Х = Получили решения системы: x =1; y = 2; z = 3.
4.Метод Гаусса. Пусть дана система m линейных уравнений с n неизвестными:
Полагая, что в системе коэффициент a11 отличен от нуля (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x1). Преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x1 с помощью эквивалентных преобразований описанным выше способом. В полученной системе
считая, что
при условии Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев: 1) если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна; 2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной; 3) если получается ступенчатая система коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна. Рассмотрим квадратную систему: У этой системы коэффициент a11 отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x1 не равен нулю. Проведем следующие преобразования системы: 1) поскольку a11¹ 0, первое уравнение оставим без изменений; 2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4; 3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3; 4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5. Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x1 (это и являлось целью преобразований 1 – 4): Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде матрицы
Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы, которую иногда называют просто матрицей системы. Системе (2) соответствует расширенная матрица
Преобразуем эту матрицу следующим образом: 1) первые две строки оставим без изменения, поскольку элемент a22 не равен нулю; 2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей; 3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой. В результате получится матрица, соответствующая системе, у которой неизвестная x1 исключена из всех уравнений, кроме первого, а неизвестная x2 — из всех уравнений кроме первого и второго:
Теперь исключим неизвестную x3 из четвертого уравнения. Для этого последнюю матрицу преобразуем так: 1) первые три строки оставим без изменения, так как a33 ¹ 0; 2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой: Полученная матрица соответствует системе
Из последнего уравнения этой системы получаем x4 = 2. Подставив это значение в третье уравнение, получим x3 = 3. Теперь из второго уравнения следует, что x2 = 1, а из первого — x1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x4, затем x3 и т. д.). Определение: Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей. Матрица коэффициентов системы (4) – треугольная матрица. Замечание: Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна. Рассмотрим другой пример: Проведем следующие преобразования расширенной матрицы системы: 1) первую строку оставим без изменения; 2) вместо второй строки запишем разность между второй строкой и удвоенной первой; 3) вместо третьей строки запишем разность между третьей строкой и утроенной первой; 4) четвертую строку заменим разностью между четвертой и первой; 5) пятую строку заменим разностью пятой строки и удвоенной первой. В результате преобразований получим матрицу
Оставив без изменения первые две строки этой матрицы, приведем ее элементарными преобразованиями к следующему виду:
Если теперь, следуя методу Гаусса, который также называют и методом последовательного исключения неизвестных, с помощью третьей строки привести к нулю коэффициенты при x3 в четвертой и пятой строках, то после деления всех элементов второй строки на 5 и деления всех элементов третьей строки на 2 получим матрицу
Каждая из двух последних строк этой матрицы соответствует уравнению 0x1+0x2+0x3+0x4+0x5 = 0. Это уравнение удовлетворяется любым набором чисел x1, x2, ¼, x5, и его следует удалить из системы. Таким образом, система с только что полученной расширенной матрицей эквивалентна системе с расширенной матрицей вида
Последняя строка этой матрицы соответствует уравнению Рассмотрим прямоугольную матрицу A, у которой число столбцов m больше, чем число строк n. Такую матрицу A назовем ступенчатой. Очевидно, что матрица (6) — ступенчатая матрица. Если при применении эквивалентных преобразований к системе уравнений хотя бы одно уравнение приводится к виду 0x1 + 0x2 + ¼ 0xn = bj (bj ¹ 0), то система несовместна или противоречива, так как ни один набор чисел x1, x2, ¼, xn не удовлетворяет этому уравнению. Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к ступенчатому виду и при этом система не получается противоречивой, то система совместна и является неопределенной, то есть имеет бесконечно много решений. В последней системе можно получить все решения, придавая конкретные числовые значения параметрам С1 и С2. Определение: Те переменные, коэффициенты при которых стоят на главной диагонали ступенчатой матрицы (это значит, что эти коэффициенты отличны от нуля), называются основными. В рассмотренном выше примере это неизвестные x1, x2, x3. Остальные переменные называются неосновными. В рассмотренном выше примере это переменные x4, и x5. Неосновным переменным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере. Основные переменные единственным образом выражаются через неосновные переменные. Определение: Если неосновным переменным приданы конкретные числовые значения и через них выражены основные переменные, то полученное решение называется частным решением. Определение: Если неосновные переменные выражены через параметры, то получается решение, которое называется общим решением. Определение: Если всем неосновным переменным приданы нулевые значения, то полученное решение называется базисным. Замечание: Одну и ту же систему иногда можно привести к разным наборам основных переменных. Так, например, можно поменять местами 3-й и 4-й столбцы в матрице (6). Тогда основными будут переменные x1, x2, x4, а неосновными – x3 и x5. Определение: Если получены два различных набора основных переменных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число переменных, называемое рангом системы. Рассмотрим еще одну систему, имеющую бесконечно много решений: Проведем преобразование расширенной матрицы системы по методу Гаусса:
Как видно, мы не получили ступенчатой матрицы, однако последнюю матрицу можно преобразовать, поменяв местами третий и четвертый столбцы: Эта матрица уже является ступенчатой. У соответствующей ей системы две неосновные переменные – x3, x5 и три основные – x1, x2, x4. Решение исходной системы представляется в следующем виде:
Приведем пример системы, не имеющей решения:
Преобразуем матрицу системы по методу Гаусса:
Последняя строка последней матрицы соответствует не имеющему решения уравнению 0x1 + 0x2 + 0x3 = 1. Следовательно, исходная система несовместна.
Лекция № 3. Тема: Векторы. Скалярное, векторное и смешанное произведение векторов План: 1. Понятие вектора. Коллинарность, ортогональность и компланарность векторов. 2. Линейная операция над векторами. 3. Скалярное произведение векторов и его применение 4. Векторное произведение векторов и его применение 5. Смешанное произведение векторов и его применение 1. Понятие вектора.Коллинарность, ортогональность и компланарность векторов.
 с начальной точкой А и конечной точкой В. с начальной точкой А и конечной точкой В.
Обозначение: Определение: Длиной или модулем вектора Определение: Вектор называется нулевым, если начало и конец вектора совпадают. Определение: Вектор единичной длины называется единичным. Определение: Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( Замечание: 1.Коллинеарные векторы могут быть направлены одинаково или противоположно. 2. Нулевой вектор считается коллинеарным любому вектору. Определение: Два вектора называются равными, если они коллинеарные, одинаково направлены и имеют одинаковые длины ( Определение: Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях 2. Линейные операции над векторами: Произведением вектора Противоположным вектором – Суммой двух векторов Сумму двух векторов можно построить также по правилу параллелограмма, где вектор Аналогично определяется сумма нескольких векторов. Например, суммой четырех вектор Вектор
Разностью двух векторов Замечание: в параллелограмме, построенном на векторах Определение: Координатами вектора
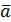 (x, y)), а в пространстве Oxyz – три числа x, y, z ( (x, y)), а в пространстве Oxyz – три числа x, y, z ( 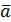 (x, y, z)) (x, y, z))
В соответствии с приведенными выше операциями над векторами, имеем: пусть даны векторы 1. 2. 3. 4. Аналогично, для вектора в пространстве 1. 2. 3. 4. |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 1642; Нарушение авторского права страницы