
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Запись квадратичной формы в матричном виде
Определение: Пусть при этом, матрица А называется матрицей квадратичной формы, а ее ранг - рангом квадратичной формы. Пример. Определить квадратичную форму с матрицей
Определение: Квадратичная форма называется симметрической, если
Приведение квадратичной формы к каноническому виду. Каноническим видом квадратичной формы называется ее выражение в виде суммы квадратов координат некоторого вектора из Rn: Определение: Невырожденная матрица Утверждение. Для каждой симметрической квадратичной формы существует линейное преобразование Используя данное утверждение в левой части Исследование на положительную (отрицательную) определенность. Определение: Симметрическая квадратичная форма, или, что, в сущности, то же – симметрическая матрица, называется положительно (отрицательно) определенной, если для всех ненулевых Утверждение. Собственные значения положительно (отрицательно) определенной матрицы строго положительны (отрицательны). Утверждение. (Критерий Сильвестра знаковой определенности симметрической квадратичной формы) Симметрическая квадратичная форма с матрицей 1) положительно определенной, когда все миноры матрицы
2) отрицательно определенной, когда знаки миноров матрицы
Именно знаковая определенность квадратичной формы, связанной с исследуемой функцией многих действительных переменных, позволяет идентифицировать так называемую стационарную точку функции, как точку локального минимума или максимума. Лекция № 6. Тема: Прямая линия на плоскости План: 1. Виды уравнений прямой на плоскости. 2. Угол между прямыми на плоскости, его вычисление. 3. Условие параллельности двух прямых. 4. Условие перпендикулярности двух прямых. 5. Расстояние от точки до прямой.
1. Виды уравнений прямой на плоскости. Определение.Уравнением линии называется такое уравнение, которому удовлетворяют координаты всех точек, лежащих на этой линии, и не удовлетворяют координаты ни одной точки, не лежащей на линии Обозначение: В общем виде F(x, y)=0 или y=f(x) (если возможно), где F(x, y), f(x) – некоторые функции 1. Уравнение прямой с угловым коэффициентом имеет вид y=kx+b, где k-угловой коэффициент прямой, равный k=tgα Частные случаи: ü b=0, следовательно, y=kx – уравнение прямой, проходящей через начало координат и образует острый угол α с осью OX при k=tgα > 0 и тупой угол α с осью OX при k=tgα < 0 ü α =0, следовательно, k=tg0=0, следовательно, y=b- уравнение прямой, параллельной оси OX ü α = 2. Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом Пусть дана точка A(x0, y0), которая лежит на прямой l и задан угловой коэффициент k=tgα , тогда уравнение прямой имеет вид 3. Уравнение прямой, проходящей через две точки Пусть даны две токи, принадлежащие прямой l: A(xa, ya), B(xb, yb), при чем xa≠ xb, ya≠ yb, тогда уравнение прямой имеет вид 4. Уравнение пучка прямых Если в уравнении k-произвольное число, то это уравнение определяет пучок прямых, проходящих через точку M(x, y), кроме прямых,
5. Уравнение прямой в отрезках Пусть прямая l отсекает на осях координат OX и OY отрезки соответственно а≠ 0 и в≠ 0.
 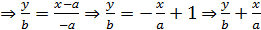 =1 =1
6. Общее уравнение прямой Имеет вид Ax+By+C=0, где А и В – одновременно не равны 0 т. е. А2+В2≠ 0 Частные случаи: ü В=0, A≠ 0 ü Пусть В≠ 0 (Обозначим a. Если A≠ 0 и С ≠ 0, то y=kx+b-уравнение прямой с угловым коэффициентом. b. Если A≠ 0 и С =0, то y=kx – уравнение прямой, проходящей через начало координат c. Если A=0 и С ≠ 0, то y=b – уравнение прямой, параллельной оси OY d. Если A=0 и С=0, то y=0 – уравнение оси OX 7.Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Заданы точка М(x0, y0) и ненулевой вектор Вектор Это уравнение можно записать в виде Ax+By+C=0, где А и В- координаты нормального вектора, С= - Ax0 – By0 – свободный член.
Угол между двумя прямыми. Пусть даны две прямые Обозначим Тогда угол между этими прямыми определяется по формуле Данный угол получается поворотом прямой
3. Условие параллельности прямых Если прямые Если прямые заданы общими уравнениями 4. Условие перпендикулярности прямых Если прямые Если прямые заданы общими уравнениями |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 1018; Нарушение авторского права страницы