Классификация изолированных особых точек
Точка  называется изолированной особой точкой функции
называется изолированной особой точкой функции  , если
, если  аналитическая в “проколотой” окрестности точки
аналитическая в “проколотой” окрестности точки  , т.е. на множестве
, т.е. на множестве  , а точка
, а точка  является особой точкой функции
является особой точкой функции  .
.
Другими словами, точка z0 называется изолированной особой точкой функции  , если существует такая окрестность точки
, если существует такая окрестность точки  , в которой нет других особых точек функции
, в которой нет других особых точек функции  .
.
Классификация изолированных особых точек следующая: устранимая особая точка, полюс порядка  , существенно особая точка.
, существенно особая точка.
Замечание. Бесконечно удаленная особая точка  является изолированной особой точкой для функции
является изолированной особой точкой для функции  , если существует окрестность
, если существует окрестность  точки
точки  , в которой нет других особых точек, за исключением бесконечно удаленной точки. Другими словами, у функции
, в которой нет других особых точек, за исключением бесконечно удаленной точки. Другими словами, у функции  не существует неограниченно возрастающей последовательности особых точек. Чтобы определить характер изолированной особой точки
не существует неограниченно возрастающей последовательности особых точек. Чтобы определить характер изолированной особой точки  для функции
для функции  нужно выполнить замену переменной
нужно выполнить замену переменной  и определить характер
и определить характер 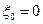 для функции
для функции  , который совпадает с характером точки
, который совпадает с характером точки  для функции
для функции  . Поэтому достаточно научиться определять характер конечной точки.
. Поэтому достаточно научиться определять характер конечной точки.
Если главная часть ряда Лорана (3.1.1) функции  в окрестности изолированной особой точки
в окрестности изолированной особой точки 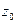 отсутствует, то
отсутствует, то 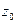 называется устранимой особой точкой.
называется устранимой особой точкой.
Другими словами, 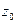 - устранимая особая точка
- устранимая особая точка 
 в окрестности точки
в окрестности точки  .
.
В этом случае существует  . Если функция не определена в точке
. Если функция не определена в точке  , то ее можно доопределить по непрерывности, положив
, то ее можно доопределить по непрерывности, положив  .
.
Пример 3.2.1. Для функции  найти все особые точки и определить их характер.
найти все особые точки и определить их характер.
Решение. Функция  имеет единственную конечную особую точку
имеет единственную конечную особую точку  . Разложим в ряд Лорана функцию
. Разложим в ряд Лорана функцию  в окрестности точки
в окрестности точки  , используя известное разложение,
, используя известное разложение,
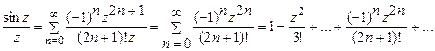 .
.
Поскольку главная часть отсутствует,  - это устранимая особая точка.
- это устранимая особая точка.
Для определения характера точки  , полагаем
, полагаем  , получим:
, получим:
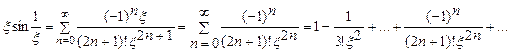 . Так как главная часть ряда Лорана содержит бесконечное число членов, то
. Так как главная часть ряда Лорана содержит бесконечное число членов, то  - это существенно особая точка, а, следовательно,
- это существенно особая точка, а, следовательно, 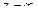 - существенно особая точка.
- существенно особая точка.
Полюс порядка  . Нули функции
. Нули функции
Если главная часть ряда Лорана функции  в окрестности ее изолированной особой точки
в окрестности ее изолированной особой точки  содержит конечное число членов:
содержит конечное число членов:  для всех
для всех 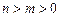 , причем
, причем 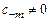 , то
, то  - называется полюсом порядка
- называется полюсом порядка  .
.
В окрестности полюса верно представление
 , где
, где 
 аналитическая в окрестности точки
аналитическая в окрестности точки  функция, причем
функция, причем  .
.
Из такого представления функции  вблизи полюса порядка
вблизи полюса порядка  видно, что
видно, что  неограниченно возрастает при стремлении
неограниченно возрастает при стремлении  к
к  .
.
Обратно: Если  изолированная особая точка
изолированная особая точка  и
и  (независимо от способа стремления
(независимо от способа стремления  к
к  ), то
), то  - полюс
- полюс  .
.
Точка  - нуль
- нуль  -го порядка функции
-го порядка функции  , если
, если  ,
, 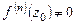 . В нуле
. В нуле  -го порядка
-го порядка  и
и  .
.
Пример 3.2.2. Для функции  найти нули и определить их порядок.
найти нули и определить их порядок.
Решение. Нулями функции  будут числа
будут числа  , где
, где  - любое целое число. Находим производные до тех пор, пока не встретится производная, для которой
- любое целое число. Находим производные до тех пор, пока не встретится производная, для которой  не являются нулями. В данном случае,
не являются нулями. В данном случае,  ,
,  . Отсюда
. Отсюда  являются нулями второго порядка.
являются нулями второго порядка.
Характер особой точки для функции  . Пусть точка
. Пусть точка  является нулем порядка
является нулем порядка  для функции
для функции 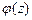 и нулем порядка
и нулем порядка  для функции
для функции  , тогда
, тогда 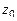 является для функции
является для функции  полюсом порядка
полюсом порядка  , если
, если  , устранимой особой точкой, если
, устранимой особой точкой, если  , нулем порядка
, нулем порядка  , если
, если  .
.
Пример 3.2.3. Для функции  найти все особые точки и определить их характер.
найти все особые точки и определить их характер.
Решение. Сначала находим нули знаменателя. Нулями функции  будут числа
будут числа  , где
, где  - любое целое число. В примере 3.2.2 было установлено, что
- любое целое число. В примере 3.2.2 было установлено, что  являются нулями второго порядка. Однако точка
являются нулями второго порядка. Однако точка  является также нулем первого порядка для числителя. Отсюда делаем вывод, что
является также нулем первого порядка для числителя. Отсюда делаем вывод, что  является простым полюсом для функции
является простым полюсом для функции 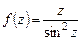 , а
, а  при
при  - полюсы второго порядка. Точка
- полюсы второго порядка. Точка  не является изолированной особой точкой, поскольку
не является изолированной особой точкой, поскольку  . Поэтому характер точки
. Поэтому характер точки  не определяется.
не определяется.
Существенно особая точка
Точка  называется существенно особой точкой функции
называется существенно особой точкой функции  , если главная часть ряда Лорана функции
, если главная часть ряда Лорана функции  в окрестности ее изолированной особой точки
в окрестности ее изолированной особой точки  содержит бесконечно много членов, т.е. бесконечное число коэффициентов
содержит бесконечно много членов, т.е. бесконечное число коэффициентов  в разложении (3.1.1).
в разложении (3.1.1).
Пример 3.2.4. Для функции  определить характер точки
определить характер точки  .
.
Решение. Используя известное разложение 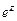 , находим разложение
, находим разложение 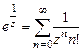 .Так как главная часть содержит бесконечное число членов, то точка
.Так как главная часть содержит бесконечное число членов, то точка  является существенно особой точкой.
является существенно особой точкой.
Пример 3.2.5. Определить характер  для функции
для функции  .
.
Решение. Выполнив замену переменной  , получим функцию
, получим функцию  . Определим характер точки
. Определим характер точки  . Как было показано в примере 3.2.4 точка
. Как было показано в примере 3.2.4 точка  является существенно особой точкой для функции
является существенно особой точкой для функции 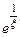 . Поэтому
. Поэтому  также является существенно особой точкой для функции
также является существенно особой точкой для функции  .
.
Пример 3.2.6. Определить характер 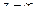 для следующих функций: а)
для следующих функций: а) 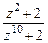 ; б)
; б)  ; в)
; в)  .
.
Решение. Полагая  , получим:
, получим:  ;
;  .
.
а) Точка  является нулем восьмого порядка функции
является нулем восьмого порядка функции  , следовательно, точка
, следовательно, точка  - нуль восьмого порядка заданной функции.
- нуль восьмого порядка заданной функции.
б) Точка  - полюс четвертого порядка функции
- полюс четвертого порядка функции  , поэтому точка
, поэтому точка  является полюсом четвертого порядка для данной функции.
является полюсом четвертого порядка для данной функции.
в) Разлагая заданную функцию в степенной ряд, получим  . Таким образом,
. Таким образом,  - существенно особая точка функции
- существенно особая точка функции  .
.
8.0.1.Определить характер всех конечных особых точек а)  ; б)
; б)  ; в)
; в) 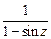 ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж).
; ж).  ; з)
; з)  .
.
8.0.2. Доказать, что  , если
, если  .
.
Ответы
8.0.1.а) z=0 – полюс второго порядка; б)  ,
,  – полюсы первого порядка; в)
– полюсы первого порядка; в)  – полюсы второго порядка; г)
– полюсы второго порядка; г) 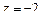 – существенно особая точка; д)
– существенно особая точка; д)  – существенно особая точка; е)
– существенно особая точка; е)  – существенно особая точка; ж)
– существенно особая точка; ж)  ,
,  - нуль первого порядка;
- нуль первого порядка;  ,
,  – полюсы первого порядка; з)
– полюсы первого порядка; з)  – полюс второго порядка.
– полюс второго порядка.
Теория вычетов
Вычет
Пусть  - изолированная особая точка функции
- изолированная особая точка функции  . Комплексное число
. Комплексное число  , где
, где  - замкнутый контур, который можно стянуть к
- замкнутый контур, который можно стянуть к  , оставаясь в кольце аналитичности функции
, оставаясь в кольце аналитичности функции  , называется вычетом
, называется вычетом  в точке
в точке  .
.
Очевидно,  в разложении (3.1.1).
в разложении (3.1.1).

