СПОСОБЫ ПРОЕЦИРОВАНИЯ 1.1. Общие понятия метода проецирования

ВВЕДЕНИЕ

Начертательная геометрия является основой графической грамотности, необходимой для современного уровня технического творчества. Она развивает логическое мышление и пространственное воображение, способность мысленно представлять форму предмета по плоскому изображению. Начертательная геометрия изучает методы изображения пространственных фигур по чертежу и алгоритмы решения позиционных, метрических и конструкционных задач.

Аппаратом начертательной геометрии является чертежно-графическая модель существующих или задуманных предметов реального мира. Изучение начертательной геометрии позволяет совершенствовать способность читать чертежи пространственных форм.

Современные инженеры, работающие в различных областях промышленности должны владеть теоретическими основами геометрического моделирования, уметь читать и анализировать чертежи. Знания, умения и навыки, приобретенные при изучении начертательной геометрии необходимы для изучения общеинженерных и специальных технических дисциплин, а также в инженерной деятельности.

Данное пособие разработано в соответствии с учебной программой курса «Инженерная и машинная графика». Оно содержит теоретический материал по начертательной геометрии, контрольные вопросы и задания для самостоятельного решения и демонстрирует возможности использования ПЭВМ для решения ряда задач начертательной геометрии и черчения.

Учебное пособие предназначено для студентов технических вузов и курсантов военных инженерных институтов.

Автор выражает благодарность сотрудникам кафедры ИиМГ Т.В. Кузьминой и В.Ф. Корзникову за помощь в техническом и графическом оформлении данного пособия.

СПОСОБЫ ПРОЕЦИРОВАНИЯ 1.1. Общие понятия метода проецирования

Операция проецирования является основой построения любого изображения.

Метод проекций заключается в проецировании каждой точки геометрического объекта на плоскость.

Рассмотрим точку А - геометрический объект. Зададим неко
торую плоскость П - плоскость проекций и точку S, не принадле
жащую П — центр проекций
(рис. 1.1). Спроецируем точку А
на плоскость П, проведем через
точки S и А проецирующую
прямую SA. Точка А_п пересече
ния проецирующей прямой SA с
плоскостью П есть проекция
точки А. Плоскость П и центр
S - аппарат проецирования.
В зависимости от выбора аппа
рата проецирования различают
центральное и параллельное Рис. 1.1

проецирование.

Центральное проецирование

Аппаратом центрального проецирования является плоскость проекции л и центр проецирования - точка S, причем S не принадлежит л. Сущность способа заключается в том, что все проецирующие лучи исходят из центра S.

Рассмотрим ряд произвольных точек и определим их центральные проекции (рис. 1.2).

Рис. 1.2. Центральное проецирование

Для этого из центра S через точки А и В проведем проецирующие лучи до пересечения с плоскостью проекций. А_п и В_п — проекции точек А и В на плоскость проекций П.

Если для некоторой точки К проецирующий луч оказался параллельным плоскости проекций л, то проекция К_п находится в несобственной точке, т. е. К_п удалена в бесконечность.

Параллельное проецирование

Аппаратом параллельного проецирования является плоскость проекций л и заданное направление проецирования s. Центр проецирования S удален в бесконечность. Сущность способа заключается в том, что все проецирующие лучи параллельны друг другу. Параллельное проецирование является частным случаем центрального проецирования.

Определим параллельные проекции точек. А и В (рис. 1.3а).

Для этого через точки А и В параллельно направлению проецирования проведем проецирующие лучи до пересечения с плоскостью л и найдем проекции точек А_п и В_п _.

Обратим внимание, что каждой точке пространства соответствует проекция на плоскости. Однако каждой проекции на плоскости соответствует бесконечное множество точек пространства,

т. е. проекция точки на плоскость не определяет ее положение в пространстве.

1.3а. Параллельное проецирование

Для однозначного определения точки в пространстве необходимо иметь два направления проецирования s \ и s ₂ (рис. 1.36). Тогда две проекции А_1п и A _2п на плоскости однозначно определяют ее положение в пространстве.

свойства оригинала сохраняются и на проекции. Такие неизменные свойства называются инвариантными (независимыми). Перечислим их без доказательства.

1. Проекция точки есть точка.

2. Проекция прямой есть прямая (в общем случае).

3. Не изменяется взаимная принадлежность геометрических
объектов и их проекций.

4. Проекции отрезков взаимно параллельных прямых парал
лельны.

5. Проекция точки пересечения линий есть точка пересече
ния проекций этих линий.

6. При прямоугольном проецировании прямой угол проеци
руется без искажения, если одна из его сторон параллельна плос
кости проекций, а другая ей не перпендикулярна.

Рис. 1.36. Параллельное проецирование

ТОЧКА

Эпюр Мошка

Ортогональное или прямоугольное проецирование является частным случаем параллельного (косоугольного) проецирования. Направление проецирующих лучей в ортогональном проецировании перпендикулярно плоскости проекций.

Метод ортогонального проецирования на две взаимно перпендикулярные плоскости называется методом Монжа. Гаспар Монж (1746-1818) - француз, основоположник начертательной геометрии.

Рис. 2.1. Система двух плоскостей проекций

Зададим две взаимно перпендикулярные плоскости проекций П1^П2 (рис. 2.1): П1 - горизонтальная плоскость проекций, П2 -фронтальная плоскость проекций. Линия пересечения плоскостей называется осью проекций и обозначается, x₁₂.

Четыре двухгранных угла, па которые плоскости делят пространство, называются четвертями.

Спроецируем точку А, произвольно выбранную в первой четверти, в данной системе плоскостей проекций. Направление лучей проецирования S1, перпендикулярно П1 и S2 перпендикулярно л₂. А\ - горизонтальная проекция точки А, А₂ - фронтальная про екция точки А. Проецирующие лучи АА1 и АА2 образуют плоскость, которая пересекает плоскость проекций по прямым А_ХА1 и Ах А₂. Эти прямые перпендикулярны к оси х₁₂ и называются ли ниями проекционной связи.

Повернем плоскость П1 вокруг оси х₁₂ до совмещения с П2 на 90° в направлении, указанном на чертеже (см. рис. 2.1). Получим одну плоскость — плоскость чертежа или эпюр (от фр. epures— чертеж) (рис. 2.2).

	Аг
Х12 Ах	• ха 0
	уа
	A1
П1

Рис. 2.2. Эпюр точки

Эпюром точки называется чертеж, на котором изображены две проекции точки, расположенные в проекционной связи.

Две проекции точки вполне определяют ее положение в пространстве. Если из проекций А1 и А2 восставить перпендикуляры

к плоскостям проекций, то точка А определится однозначно. Точка А в пространстве определена тремя координатами х, у, z, которые можно измерять на эпюре.

2.2. Ортогональная система трех плоскостей проекций

В практике для изображения геометрических объектов, решения некоторых задач возникает необходимость использовать третью плоскость проекций л₃, перпендикулярную П1 и П2. Плоскость П₃ - профильная плоскость проекций. А₃ - профильная проекция точки А.

Система трех плоскостей проекций делит пространство на 8 октантов, октанты принято нумеровать римскими цифрами (рис. 2.3).

Рис. 2.3. Система трёх плоскостей проекций 12

В первом октанте все координаты положительные.

Чтобы перейти к чертежу па плоскости, совместим все три плоскости в одну плоскость П₂ по направлениям, указанным па чертеже. Плоскость П1 вращаем вокруг оси х₁₂ на 90°, плоскость П3 - вокруг оси z₂₃ на 90° против часовой стрелки. При этом ось у раздваивается.

Получается комплексный чертеж точки (рис. 2.4).

Рис. 2.4. Комплексный чертеж точки

На комплексном чертеже все проекции точки А1, А2, А3 находятся в проекционной связи. Каждая проекция точки определяется двумя координатами:

А1-Х, У1;

А2-Х, Z;

А3-У3, Z.

В данном примере Х= 30, у = 25, z = 35. Третья профильная проекция точки может быть определена по линиям связи от проекций А1 и А2. Проекции А2 и А3, расположены на одной горизон-гальной линии связи, которая определяется координатой z (отрезок ОА z ), а от горизонтальной проекции А\ проводим линию связи

перпендикулярно оси у1, отрезок OA _у (координата у) переносим против часовой стрелки на горизонтальную ось у₃ и восставляем перпендикуляр (линию связи) до пересечения с горизонтальной линией связи от а2. Координата у от А1 переносится на горизонтальную ось y 3 всегда против часовой стрелки, так как плоскость П₃ при совмещении с П3 разворачивается против часовой стрелки.

Профильную проекцию А3 можно определить, откладывая координаты на соответствующих осях проекций с учетом знака.

Знаки координат зависят от того, в каком октанте расположена точка (табл. 1).

Таблица 1

Координата	Октанты
Координата	I	II	III	IV	V	VI	VII	VIII
х	+	+	+	+	-	-	-	-
У	+	-	-	+	+	-	-	+
2	+	+	-	-	+	+	-	-

2.3. Точки разных углов пространства. Точки частного положения

Если точка не принадлежит ни одной плоскости проекций, она занимает общее положение.

Если точка расположена в плоскости проекций или на оси проекций, она занимает частное положение.

Рассмотрим ряд точек общего положения (рис. 2.5, 2.6).

Точка В (х = 30, у = 25, z = -35) находится в IV октанте. Проекция В1 расположена ниже оси х на положительном направлении оси у. Проекция В₂ расположена тоже ниже оси х на отрицательном направлении оси z. В₃ определяется по линиям связи от В1 и В2 или по координатам У= 25, z = -35.

Точка С (х = -30, у = 40, z = 30) находится в V октанте. Проекция С1 расположена справа от оси z на отрицательном направлении оси х и ниже оси х на положительном направлении оси у. Проекция С₂ расположена выше оси х на положительном направлении оси z.

Точка L (х = 0, у = 0, z = 40) расположена на оси z.

Сз определяется по линиям связи от С1 и С2 или по координатам У = 40, z = 30.

Рассмотрим точки частного положения, расположенные на плоскостях и осях проекций.

Если координата Х = 0, то точка принадлежит плоскости П₃.

Если координата У= 0, то точка принадлежит плоскости П₂.

Если координата z = 0, то точка принадлежит плоскости П1.

Рассмотрим ряд точек частного положения (рис. 2.7, 2.8).

Рис. 2.7. Точки частного положения

Точка D (х = 0, у = 30, z = 20) принадлежит плоскости П₃ и совпадает с профильной проекцией D3 проекции D 1 и D2 расположены соответственно на осях у и z.

Точка Е (х = 30, у = 0, z = 35) принадлежит плоскости П₂ и совпадает с фронтальной проекцией Е₂, проекции Е1 и Е3 расположены соответственно на осях Х и Z.

Точка К (х = 40, у = 25, z = 0) принадлежит плоскости П1 и совпадает с горизонтальной проекцией К1, проекции К2 и К3, расположены соответственно на осях х и у.

Рис. 2.8. Комплексный чертеж точек частного положения

Вопросы и задания для самоконтроля

1. Сколько проекций точки вполне определяют ее положение в
пространстве?

2. Какая координата точки определяет ее расстояние:

а) до горизонтальной плоскости проекций П1

б) до фронтальной плоскости проекций П2

в) до профильной плоскости проекций П3?

3. Выполнить комплексный чертеж точек и указать, в каком
октанте они расположены:

а)А(х= 50, у = -10, z = -30);

б) В (х =-40, у= -20, z=35);

в) С (х = - 20, у = - 30, z = - 45);

г) D (Х=-30, У=0, Z=-50)

д) Е (х = 0, у = - 40, z = 25).

ПЛОСКОСТЬ

4.1. Способы задания плоскости

Плоскость считается заданной, если из всех точек пространства можно выделить только те точки, которые принадлежат данной плоскости. Плоскость на чертеже может быть определена следующими способами (каждый из способов допускает переход к любому другому способу):

Рис. 4.16. Прямая и точка

1) тремя точками, не лежащими на одной прямой (рис. 4.1 а);

2) прямой и точкой вне прямой (рис. 4.16);

3) двумя пересекающимися прямыми (рис. 4.1 в);

4) двумя параллельными прямыми (рис. 4.1 г);

5) любой плоской фигурой - отсеком пространства (рис. 4.1д);

6) следами плоскости (рис. 4.2).

Рис. 4.1 д. Фигура

Следы плоскости — это линии пересечения плоскости с плоскостями проекций.

Линия пересечения плоскости с плоскостью П1 называется го ризонтальным следом плоскости Q1 с плоскостью П2 - фрон тальным следом Q 2, с плоскостью П3 - профильным следом Q 3.

Точки пересечения следов на осях проекций называются точками схода следов Q_x, Q_y, Q_Z.

Отрезки OQ_Z , OQ_y, OQ_Z, отсекаемые осями проекций, называют параметрами плоскости (рис. 4.2).

Главные линии плоскости

Кроме прямых общего положения, в плоскости можно выде-лить линии частного положения, которые называют главными линиями плоскости. Главные линии плоскости - это линии уровня и линии наклона плоскости.

1. Горизонтали плоскости h - это прямые, принадлежащие какой-либо плоскости и параллельные плоскости л, (рис. 4.6).

Рис. 4.6. Горизонтали плоскости

На эпюре фронтальная проекция горизонтали h₂ параллельна оси х, а горизонтальная проекция горизонтали h₁ параллельна

горизонтальному следу плоскости h || Т1, т. е. горизонтальный след плоскости - это тоже её горизонталь.

2. Фронтали плоскости f - это прямые, принадлежащие какой-либо плоскости и параллельные плоскости П2 (рис. 4.7).

На эпюре горизонтальная проекция фронтали f1, параллельна оси x12, а фронтальная проекция фронтали параллельна фронтальному следу плоскости f2 || Г2, т. е. фронтальный след плоскости - это тоже фронталь плоскости.

Рис. 4.7. Фронтали плоскости

3. Профильные прямые плоскости р - это прямые, принадлежащие какой-либо плоскости и параллельные плоскости П3 (рис. 4.8).

На эпюре горизонтальная и фронтальная проекции профиль-ной прямой р1 и p 2 перпендикулярны оси х, а профильная проекция профильной прямой р₃ параллельна профильному следу р₃||0₃), т. е. профильный след плоскости - это тоже её профиль-

ная прямая.

4. Линия наибольшего наклона плоскости L - это прямая, принадлежащая плоскости и перпендикулярная к соответствующей линии уровня плоскости. С помощью линии наибольшего наклона определяется угол наибольшего наклона плоскости к соответствующей плоскости проекций.

Линия L, перпендикулярная горизонталям плоскости, определяет угол наклона плоскости к плоскости П1 (рис. 4.9).

Если плоскость задана следами, то горизонтальная проекция линии наибольшего наклона плоскости перпендикулярна гори-зонтальному следу λ 1 (рис. 4.9). Если плоскость задана другим способом, необходимо построить горизонталь плоскости, тогда горизонтальная проекция линии наибольшего наклона определяется прямой, перпендикулярной горизонтальной проекции гори-зонтали (l 1 перпендик. h 1).

Аналогично можно построить линии наибольшего наклона к другим плоскостям проекций.

Рис. 4.8. Профильные прямые плоскости 40

СЛЫЮ ПЛОСКОСТИ.

Параллельные плоскости

Плоскости параллельны, если две пересекающиеся прямые од ной плоскости соответственно параллельны двум пересе кающимся прямым другой плоскости (рис. 4.10).

Рис. 4.10. Параллельные плоскости

При задании плоскости следами две плоскости параллельны, если параллельны их одноимённые следы (см. рис. 4.10).

Рис. 4.9. Линия наибольшего наклона плоскости

Пример 1. Через точку К провести плоскость, параллельную заданной плоскости T (рис. 4.11).

X -

Рис. 4.11

Решение. Через точку проведем горизонталь h, параллельную заданной плоскости Т, т. е. h 1 параллельна Т1. Найдём фронтальный след горизонтали N ( N 1, N 2). Через фронтальный след горизонтали N ₂ проведём фронтальный след искомой плоскости Г₂ параллельно фронтальному следу плоскости Т₂ и определим точку схода следов Г_х. Проведем горизонтальный след плоскости Г₁ из Г_x. параллельно горизонтальному следу h₁.

4.5.2. Прямая линия, параллельная плоскости

Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в плоскости (рис. 4.12).

Через каждую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости Р.

Рис. 4.12. Прямая линия, параллельная плоскости

Пример 2. Через точку С провести прямую а, параллельную плоскости Р (рис. 4.13).

Решение. Одну из проекций искомой прямой а₂ проведём произвольно через точку С₂. Определим в данной плоскости Р

прямую, параллельную прямой а. Горизонтальная проекция прямой а₁ будет параллельна горизонтальной проекции прямой в плоскости: а₂||(1₂ 2₂) и а₁||(l₁ 2₁).

4.5.3. Пересекающиеся плоскости

Две плоскости пересекаются по прямой линии, для построения которой достаточно определить или две общие для плоскостей точки, или одну точку и направление линии пересечения.

Рассмотрим задачи на построение проекций линии пересечения плоскостей и их положения относительно плоскостей проекций.

1. Если плоскости заданы следами и следы пересекаются в пределах чертежа (рис. 4.14а), то две точки линии пересечения определяются на пересечении одноимённых следов. Точка 1 -пересечение горизонтальных следов, точка 2 - пересечение фронтальных следов. Линия l (l1l2) — линия пересечения плоскостей λ, и Σ.

Рис. 4.14а. Плоскости заданы следами

2. Один из частных случаев пересечения плоскостей, когда одна из них является проецирующей плоскостью (рис. 4.146).

Задача сводится к определению второй проекции линии, принадлежащей и проецирующей плоскости, и плоскости общего положения.

77/7,

Определяем точки пересечения соответствующего следа проецирующей плоскости с плоскостью общего положения (точки 1 и 2). По линиям связи определяем вторую проекцию. Затем необходимо определить видимость отсеков плоскости общего положения относительно линии пересечения.

Рис. 4.146. Одна из пересекающихся плоскостей- проецирующая

3. В некоторых случаях линия пересечения плоскостей является линией частного положения (рис. 4.14в).

Рассмотрим задачи на пересечение плоскостей по горизонтами. В первой задаче одна из плоскостей λ, является горизонтальной плоскостью уровня, поэтому фронтальная линия проекции пересечения h₂ совпадает со следом этой плоскости и является

(Горизонталью. Горизонтальная проекция определяется по точке 1 Пересечения следов и направлению h ₁ || λ ₁.

Рис. 4.14в. Пересечение плоскостей по линиям частного положения

В примере 2 горизонтальные следы плоскостей общего положения параллельны (λ 1 || Σ 1). Следовательно, горизонтальная проекция линии пересечения плоскостей будет параллельна им ( h 1 || λ 1 || Σ 1), а фронтальная проекция будет проходить через точку 1 пересечения фронтальных следов.

Аналогичны случаи пересечения плоскостей по фронтали. Существуют другие частные случаи пересечения плоскостей, когда линией пересечения являются проецирующие прямые.

4. Общий случай пересечения плоскостей, когда в пределах
чертежа сразу не определяются общие для данных плоскостей
точки. Для решения такой задачи используются вспомогательные
секущие плоскости обычно частного положения - или плоскости
уровня, или проецирующие.

Рассмотрим пример на рис. 4.15.

Даны две плоскости, заданные параллельными прямыми (а || b ) и треугольником AВС. Для определения двух общих точек данных плоскостей решаем задачу по следующему алгоритму:

1. Вводим первую вспомогательную горизонтальную плос-
кость уровня Σ.

2. Строим линии пересечения каждой данной плоскости со
вспомогательной (а || b ) ∩ Σ → h ^∑, ( ABC ) ∩ ∑ → h ^∑ ₁. Эти линии
являются горизонталями данных плоскостей.

3. Определяем точку пересечения линии пересечения. Точка
I- общая для данных плоскостей.

Рис. 4.15. Общий случай пересечения плоскостей 49

4. Для определения ещё одной общей точки вводим вторую
вспомогательную секущую плоскость уровня λ. Выполним те же
построения и определим вторую общую точку II.

5. Соединяем получившиеся точки I и II, которые определяют
линию пересечения плоскостей l (l ₁ l ₂).

При решении некоторых задач удобнее использовать вспомогательные проецирующие плоскости.

СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ

Преобразование проекций используется для наиболее выгодного изображения геометрических фигур при их исследовании и для решения метрических и позиционных задач. После преобразования чертежа объекты занимают частное положение относительно плоскостей проекций. Существует несколько способов преобразования проекций:

- способ замены плоскостей проекций;

- способ вращения вокруг проецирующих прямых и прямых

уровня;

- способ плоскопараллельного перемещения.

Принципиальное отличие первого способа (замены плоскостей проекций) от других заключается в том, что объект не меняет своего положения в пространстве, а вводятся новые дополнительные плоскости проекций. При использовании способов вращения и плоскопараллельного перемещения система плоскостей остаётся неизменной, а объект перемещается относительно системы плоскостей.

5.1. Способ замены плоскостей проекций

Сущность способа замены плоскостей рассмотрим на примере. На рис. 5.1 дана точка А в системе плоскостей проекций П1 / П2. Заменим одну из них, например П2, другой вертикальной плоскостью П4 ┴ П1, т.е. перейдём к новой системе плоскостей проекций П4 / П1. Определим новую фронтальную проекцию точки A 4, используя для этого неизменность координаты Z точки А, так как горизонтальная плоскость проекций П1 является общей для исходной и новой систем. На эпюре из горизонтальной проекции А1 проведём линию связи, перпендикулярную к новой оси, Х14 и отложим координату Z точки А.

Рис. 5.1. Способ замены плоскостей проекций

Способом замены плоскостей определяют натуральную вели-чину прямой и плоскости, определяют расстояние между прямыми плоскостями и т.д. При решении задач приходится менять последовательно либо одну, либо две плоскости проекций так,

чтобы геометрические объекты оказались в частном положении относительно новой системы.

Рассмотрим задачи на преобразование прямой и плоскости.

ПРИМЕР. Дана прямая АВ общего положения (рис. 5.2).

Преобразовать прямую АВ в проецирующую прямую.

лнрно прямой АВ, новая ось проекций Х45┴ A 4 B 4. Построим покую горизонтальную проекцию А₅В₅, отложив неизменную координату Y. Прямая АВ обращается в точку А₅ ≡ В₅ и является гори-юнтально проецирующей прямой в новой системе плоскостей

П4/П5.

XiE

Пример 2. Даны две параллельные прямые линии АВ и CD (рис. 5.3). Определить расстояние между ними.

Рис. 5.2

Решение. Прямую общего положения можно преобразовать в проецирующую прямую только двумя последовательными заменами плоскостей проекций, так как плоскость проекций, перпендикулярная к прямой общего положения, не будет перпендикулярна ни к П1 ни к П2. Первоначально заменим плоскость проекций П2 на П4 (┴ П1) параллельно прямой АВ, новая ось проекций х4||А1В1. Построим новую фронтальную проекцию А4В4, отложив неизменную координату Z. Прямая АВ преобразована в новой системе П1/П4 во фронталь, А4В4 - натуральная величина отрезка прямой, а угол а - угол наклона прямой к плоскости проекций П1. Затем заменим плоскость проекций П1 на П5 (┴ П4) перпендику-

Рис. 5.3

Решение. Чтобы определить расстояние между параллельными прямыми, необходимо преобразовать их в проецирующие прямые. Этого можно добиться двумя последовательными заменами плоскостей проекций. Первая замена плоскости проекций П1| на П5 — параллельно данным прямым, новая ось проекций Х₂₅|| С₂D₂ ||A 2 B 2. Прямые АВ и CD преобразованы в новой системе плоскостей проекций П₂/П₅ в горизонтали. Вторая замена плоскости проекций П₂ на П₄ - перпендикулярно прямым АВ и CD, новая ось проекций Х45 ┴ C 5 D 5 ┴ (А5В5)- На новую фрон-

тальную плоскость П₄ прямые АВ и CD проецируются в точки А₄ = В₄, С4 = D4. Измеряем расстояние между точками.

Пример 3. Дана плоскость, заданная треугольником ABC общего положения (рис. 5.4). Определить натуральную величину треугольника ABC.

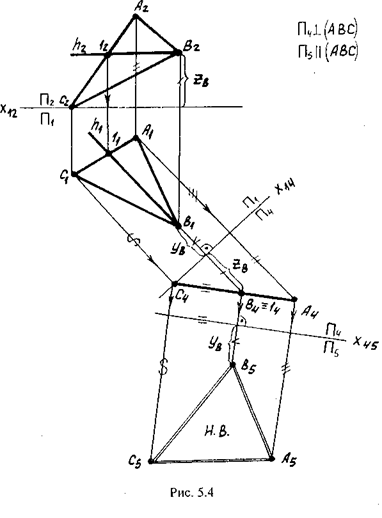
Решение. Чтобы определить натуральную величину плоскости, необходимо расположить её параллельно плоскости проекций. Плоскость общего положения невозможно сразу преобразовать в плоскость уровня, так как параллельная ей новая плоскость проекции не будет перпендикулярна ни к П1, ни к П2. По-чтому необходимо выполнить две последовательные замены плоскостей проекций, преобразовав данную плоскость сначала в проецирующую, а затем в плоскость уровня.

Заменим плоскость проекций П2 на П4 перпендикулярно треугольнику ABC. Чтобы определить направление П4, проведём в треугольнике ABC горизонталь h. Новая плоскость проекций П₄будет перпендикулярна горизонтали, новая ось проекций Х14 ┴ h 1. На линии связи откладываем неизменные координаты Z_A, Z _В, Z _С. Новая фронтальная проекция А₄ В₄ С₄ в системе плоскостей П1/П4 представляет собой прямую линию, плоскость ( ABC ) преобразо-вана во фронтально проецирующую.

Затем заменим плоскость проекций П1 на плоскость П5 параллельно треугольнику ABC, новая ось проекций Х₄₅ || А4, В4, С4 , неизменной остаётся координата Y. В новой системе плоскостей П4/П5 треугольник ABC является горизонтальной плоскостью уровня. Новая горизонтальная проекция A ₅ B ₅ C ₅ - натуральная величина треугольника АВС.

5.2. Способ вращения

Суть способа вращения состоит в том, что геометрический объект вращают в пространстве вокруг выбранной оси i до тре-буемого положения относительно плоскостей проекций. Траектории движения точек объекта являются дугами окружностей, центр которых находится на оси вращения.

НОЙ ОСИ Х12.

Рис. 5.6. Вращение прямой 65

Пример 4. Определить натуральную величину отрезка АВ прямой общего положения. Преобразовать данную прямую в проецирующую (рис. 5.6).

Решение. Чтобы определить натуральную величину отрез- ка прямой общего положения, необходимо преобразовать его в прямую уровня. Одна из проекций прямой уровня параллельна оси х12. Выбираем ось вращения i¹ перпендикулярно плоскости П1. Чтобы повернуть прямую линию на некоторый угол а, необ- ходимо повернуть на этот угол две её точки. Но задачу можно упростить, если ось вращения будет совпадать с одной из точек прямой. В нашем случае ось совпадает с точкой В. Эта точка ос-таётся неподвижной. Остаётся повернуть точку А до положения, при котором отрезок АВ окажется параллельным плоскости П₂. Проекция А¹₁ В¹₁ \\ х12, на фронтальной проекции точка А₂ переме- щается параллельно оси Х12. Данная прямая линия преобразована таким вращением во фронталь. Проекция А¹₂ В¹₂ является нату- ральной величиной отрезка АВ, а угол а - угол наклона прямой к плоскости П1.

Вторым вращением преобразуем отрезок АВ в проецирующую прямую. Для этого ось вращения i² выбираем перпендикулярно плоскости П₂. Ось i² совпадает с точкой А, которая останется неподвижной при втором вращении. Повернём точку В до положения, при котором прямая займёт положение, перпендикулярное плоскости проекции П1. На фронтальной проекции А²₂ В²₂ перпендикулярна оси х12, а на горизонтальной проекции В¹₁ перемещается параллельно оси х12 и совпадает с проекцией А¹₁. Новая горизонтальная проекция прямой А²₁ В²₁ преобразуется в точку. Вторым вращением данная прямая преобразована в горизонтально проецирующую.

Пример 5. Преобразовать плоскость Т общего положения во фронтально проецирующую. Определить угол её наклона к плоскости П1 (рис. 5.7).

Решение. Чтобы повернуть плоскость вокруг какой-либо оси на угол φ, необходимо повернуть на этот угол геометрические элементы, определяющие плоскость на чертеже.

Рис. 5.7. Вращение плоскости

Для преобразования плоскости Т во фронтально проецирую-щую необходимо повернуть её на такой угол, чтобы горизонтальный след плоскости оказался перпендикулярным к оси х12- Выбираем ось вращения i перпендикулярно плоскости П1 так, чтобы в пределах чертежа определялась неподвижная точка плоскости Т— точка пересечения оси i с плоскостью Т. Эту точку 1 (1₁, 1₂) опре-деляем с помощью горизонтали плоскости h. Определяем радиус вращения горизонтального следа плоскости T - i ₁ M ₁ ┴ T ₁. Поворачиваем след плоскости Т1 перпендикулярно оси х₁₂, радиус вращения i ₁ M¹₁ || х12. Определяется новая точка схода следов плоскости Т¹_х. Для определения нового фронтального следа Т¹₂ соединяем точку схода следов Т¹_х с фронтальной проекцией неподвижной точки плоскости 1₂. Плоскость Т преобразована во Фронтально проецирующую, угол а - угол наклона плоскости Т к плоскости проекций П1.

Пример 6. Определить натуральную величину треугольника ABC способом вращения (рис. 5.8).

Решение. Первым вращением вокруг оси i, перпендикулярной плоскости П2 и совпадающей с точкой В, преобразуем треугольник ABC в горизонтально проецирующую плоскость. Повернём фронтальную проекцию треугольника ABC в положение, при котором фронталь BD будет перпендикулярна оси х. Горизонтальные проекции точек А и С перемещаются параллельно оси х, точка В неподвижна. Плоскость преобразована в горизонтально проецирующую, проекция А¹₁ В¹₁ С¹₁ - прямая линия.

Рис. 5.8. Определение натуральной величины плоскости ( ABC ) способом вращения

Вторым вращением вокруг оси i ₁, перпендикулярной плоскости П1 и совпадающей с точкой С, преобразуем треугольник ABC во фронтальную плоскость уровня. Повернём горизонтальную проекцию А¹₁ В¹₁ С¹₁ до положения, параллельного оси х,

А²₁В²₁С²₁ || Х. На фронтальной проекции точки А и В перемещаются параллельно оси х, точка С — неподвижна. Новая фронтальная проекция А²₂В²₂С²₂ является натуральной величиной треугольника ABC.

5.2.2. Вращение вокруг липни уровня

Задачу на определение натуральной величины плоской фигуры можно решить более быстрым способом, если за ось вращения кыбрать линию уровня. Одним вращением вокруг этом линии можно расположить данную плоскость параллельно одной из плоскостей проекций, вращая вокруг горизонтали — параллельно плоскости П1 вокруг фронтали - параллельно плоскости П2.

Рассмотрим пример на рис. 5.9.

Горизонталь h плоскости ( ABC ) является осью вращения i. Точки А и 1 плоскости остаются неподвижными, так как расположены на оси вращения. Задача сводится к определению натуральной величины радиусов вращения двух точек плоскости В и С. Определяем радиусы вращения этих точек: О₁ В_1┴ h ₁, О^’₁С₁┴ h ₁. Найдём натуральную величину радиуса ОВ, вращаем

его вокруг оси, перпендикулярной плоскости П2 в точке О. О₁ В¹₁ — натуральная величина ОВ, откладываем её на горизонтальной проекции радиуса, определяем положение точки В после крашения - В₀. Через В₀ и неподвижную точку 1₁ проводим прямую до пересечения с прямой О^’₁С₁. Определяем положение точки С после вращения - С₀. А₁ В₀С₀ - натуральная величина i треугольника ABC, преобразованного в горизонтальную плоскость уровня. Фронтальная проекция плоскости i треугольника в результате вращения преобразуется в прямую, совпадающую с горизонталью плоскости h.

Рис. 5.9. Вращение вокруг горизонтали

Сущность этого способа заключается в том, что все точки геометрической фигуры перемещаются в плоскостях, параллельных одной из плоскостей проекций.

Следовательно, точки движутся в плоскостях уровня, и одна из проекций геометрической фигуры перемещается без изменения формы и размеров, а на другой проекции траектории движения точек параллельны оси х.

Рассмотрим преобразование отрезка АВ прямой общего положения в проецирующую прямую (рис. 5.10). Первоначально преобразуем прямую АВ во фронталь, переместив проекцию А₁ В₁ без изменения размеров параллельно оси х (в произвольном месте). Точки прямой АВ перемещаются параллельно плоскости П1. На фронтальной проекции траектории точек параллельны оси х. Новые фронтальные проекции определяем на пересечении линий связи от А¹₁ В¹₁, с траекториями движения точек.

5.3. Способ плоскопараллельного перемещения

При использовании способа вращения фигур иногда происхо-
дит наложение изображений. Этого можно избежать, применяя
способ ппоскопараллелъпого перемещения.
Рис. 5.10. Способ плоскопараллельного перемещения

Проекция А¹₂ В¹₂ является натуральной величиной АВ, так как первым перемещением прямая преобразована во фронталь.

Второе перемещение выполним параллельно плоскости П2. Фронтальную проекцию переместим без изменений размеров перпендикулярно оси х (А²₂В²₂ ┴ Х). На горизонтальной проекции

точки движутся параллельно оси х, и отрезок АВ преобразуется в горизонтально проецирующую прямую.

Пример 7. Определить расстояние от точки S до плоскости ABC (рис. 5.11) способом плоскопараллельного перемещения.

С:

Решение. Для решения этой задачи необходимо преобразовать плоскость общего положения в проецирующую. Если одна из проекций плоскости будет преобразована в прямую линию, то можно опустить перпендикуляр из точки S и определить расстояние. Перемещаем плоскость ABC перпендикулярно плоскости П2.

прямую линию. Опускаем перпендикуляр из перемещенной точки.?, на новую фронтальную проекцию треугольника.

Вопросы и задания для самоконтроля

1. В чём заключается сущность способа перемещения плос-
костей проекций?

2. Сколько последовательных преобразований и каких нужно
выполнить, чтобы определить натуральную величину плоскости
общего положения?

3. Как движутся точки геометрического объекта при враще-
нии его вокруг осей, перпендикулярных плоскостям проекций?

4. Сколько последовательных вращений и каких нужно вы
полнить, чтобы преобразовать прямую общего положения в про-
ецирующую?

5. Определите расстояние между двумя параллельными пря-
мыми общего положения способом плоскопараллельного пере-
мещения?

6. Определите натуральную величину треугольника враще-
нием его вокруг фронтали.

Рис. 5.11

Располагаем новую горизонтальную проекцию прямоугольника А¹₁В¹₁С¹₁ без изменения формы и размера так, чтобы горизонталь h оказалась перпендикулярной плоскости П₂. На фронтальной проекции точки перемещаются параллельно оси х. Новая фронтальная проекция треугольника А¹₂В¹₂С¹₂ преобразуется в

ПОВЕРХНОСТИ

Многогранные поверхности

Развертка многогранника

Разверткой поверхности называется плоская фигура, полученная совмещением поверхности с плоскостью.

Построение разверток важно для тех видов производства, где продукция изготавливается из листового материала. При проектировании листовых конструкций выполняется построение разверток их поверхностей. При построении развертки многогранника необходимо определить натуральную величину всех его граней.

Рис. 6.4. Пересечение прямой с многогранником

Существует несколько способов построения разверток: способ нормального сечения, способ раскатки.

Рассмотрим построение развертки призмы способом нормаль-

ного сечения.

Пример 5. Дама треугольная призма (рис. 6.5). Построить развертку поверхности данной призмы.

Рис. 6.5. Развёртка призмы. Способ нормального сечения

Решение. Пересечем призму плоскостью Т перпендикулярно ее боковым ребрам. Полученное сечение (123) называется нормальным. Так как в данной задаче ребра призмы являются горизонталями, то след плоскости нормального сечения Т₁ перпендикулярен горизонтальным проекциям ребер A ₁ F _1, B ₁ D ₁, C ₁ E ₁. Определяем натуральную величину нормального сечения призмы плоскостью Т способом вращения вокруг оси i. Фигура (1¹₂, 2¹₂, 3¹₂)натуральная величина нормального сечения. Для построения развертки на горизонтальной линии отложим отрезки, равные сторонам нормального сечения: 1₀2₀≡ 1¹₂2¹₂, 2₀3₀≡ 2¹₂3¹_2, 3₀1₀≡ 3¹₂1¹₂. Ребра призмы перпендикулярны линии нормального сечения, их натуральную величину измеряем на горизонтальной плоскости (так как ребра являются горизонталями) B₀ D ₀ ≡ B ₁ D ₁, A ₀ F ₀ ≡ A ₁ F ₁, С₀Е₀≡ С₁Е₁. Полученная фигура B ₀ AoCoBoDoE ₀ FoD o является боковой поверхностью призмы. Для получения полной развертки достраиваем основания призмы в натуральную величину.

6.2. Кривые поверхности

6.2. I. Основные понятия

В начертательной геометрии кривая поверхность определяется как непрерывное множество положений перемещающейся в пространстве линии, называемой образующей. Образующая может быть прямой (линейчатая поверхность) или кривой (нелинейчатая ) линией. Движение образующей в пространстве может осуществляться по некоторому закону. Такая поверхность называется закономерной в отличие от незакономерной (случайной) поверхности. К числу условий перемещения в пространстве образующей линии относятся: перемещение по неподвижным линиям направляющим, вращательное движение вокруг неподвижной оси, винтовое перемещение и др.

Одна и та же поверхность может быть образована перемещением различных линий и согласно различным условиям. Например, боковая поверхность прямого кругового цилиндра может быть рассмотрена как результат:

- перемещения окружности вдоль некоторой оси;

- вращения некоторой образующей прямой линии вокруг оси
вращения;

- вращения некоторой кривой линии, все точки которой рав-
ноудалены от оси вращения.

Рассматривая совокупность прямолинейных образующих с совокупностью образующих окружностей получим каркас данной поверхности цилиндра.

Множество неподвижных линий, инцидентных данной поверхности и объединенных каким-либо общим признаком, называется её каркасом.

6.2.2. Задание поверхности вращения на чертеже. Точки и линии па поверхности

На чертеже поверхность изображают очерком проекций поверхности или её отдельных частей.

Задать поверхность, на чертеже - значит указать условия, позволяющие построить каждую точку этой поверхности.

Точка принадлежит поверхности, если она находится на линии, принадлежащей данной поверхности. Рассмотрим чертёж конуса и точки, принадлежащие его поверхности (рис. 6.6). Фронтальная проекция конуса задана очерковыми образующими, определяющими границы поверхности, а горизонтальная -проекцией основания конуса. Каркас конуса - это совокупность образующих прямых линий, соединяющих их вершину S и основание конуса и совокупность параллелей — окружностей различного радиуса, плоскость которых перпендикулярна оси конуса.

Рис. 6.6

Рассмотрим ряд точек на боковой поверхности конуса. Точка А расположена на очерковой образующей конуса, её горизон-тальная проекция находится на линии связи на оси конуса. Обра-

тим внимание, что очерковая образующая является фронталью, т. е. её фронтальная проекция - натуральная величина образующей конуса.

Принадлежность точек В и С поверхности конуса определяется соответственно с помощью параллели радиуса R или образующей конуса

6.2.3. Позиционные задачи па пересечение поверхности с прямой линией и плоскостью

В общем случае пересечением поверхности с плоскостью является кривая линия.

Рассмотрим конические сечения фронтально проецирующими плоскостями и горизонтальной плоскостью уровня (рис. 6.7) Обозначим угол наклона образующей к оси конуса а, а угол наклона следа плоскости - ф. В зависимости от угла наклона плоскости линией сечения может быть окружность, эллипс, парабола, гипербола. Если:

φ = 90°, линия сечения - окружность;

φ > а - эллипс;

φ = а- парабола;

φ < а - гипербола.

Если секущая плоскость проходит через вершину конуса, то сечением является треугольник.

Пример 6. Построить линию сечения конуса фронтально проецирующей плоскостью Σ (рис. 6.8).

Решение. Линией сечения в данном случае будет неполный эллипс, так как угол наклона плоскости Σ к оси конуса больше угла наклона образующей. Фронтальная проекция линии сечения совпадает со следом плоскости, так как секущая плоскость является фронтально проецирующей. Определим горизонтальную проекцию сечения. Первоначально отметим опорные точки: точка 1 на очерковой образующей является высшей точкой сечения, точки 2 и 3 на основании конуса — низшие точки. Ряд промежу-

Рис. 6.7. Сечение конуса

точных точек 4, 5, 6, 7 определяем с помощью параллелей конуса, проведённых через эти точки. Точки 8, 9 определены через образующую конуса. Полученные точки плавно соединяем с учётом видимости.

Рис. 6.8

Пример 7. Определить точки пересечения прямой а с конусом (рис. 6.9).

Рис. 6.9. Пересечение прямой с конусом 87

Решение. Для решения задачи выгоднее всего использовать вспомогательную плоскость, проходящую через вершину конуса. Для этого дополним прямую а до плоскости прямой b, пересекающейся с ней в точке 1 (см. рис. 6.9). Определим горизонтальный след вспомогательной плоскости Σ (a ∩ b). Для этого найдём следы прямых а и b - М и М¹. Отметим точки пересечения основания конуса с горизонтальным следом ∑ - точки А и В. Определилась линия сечения конуса со вспомогательной плоскостью -треугольник ABS.

На пересечении линии сечения A ₁ B ₁ S ₁ и проекции прямой а₁ находим искомые точки K₁ и L ₁, по линиям связи -точки K₂ и L ₂. Затем определяем видимость прямой относительно точек пересечения.

6.2.4. Взаимное пересечение поверхностей

Две кривые поверхности в общем случае пересекаются по пространственной кривой линии. Для построения этой линии, в зависимости оттого, как заданы поверхности, применяют метод вспомогательных секущих плоскостей или метод секущих сфер.

При использовании метода секущих плоскостей вводится ряд вспомогательных плоскостей, пересекающих каждую поверхность по линии, простой по построению (окружность или прямая). На пересечении линий пересечения определяются общие для поверхностей точки. Иногда целесообразно использовать вспомогательные секущие сферы, так как сфера, центр которой располагается на оси поверхности вращения, пересекает ее по окружности (рис. 6.10).

Использование метода сфер требует выполнения следующих условий:

1.Оси поверхностей вращения должны пересекаться. Центр секущих сфер выбирается в точке пересечения осей.

2. Оси пересекающихся поверхностей вращения должны быть параллельны какой-либо плоскости проекции.

Рис. 6.10

Пример 8. Определить линию пересечения вертикального конуса и горизонтального цилиндра (рис. 6.11).

Решение. Для решения задачи удобно использовать способ вспомогательных секущих плоскостей. Если рассекать обе поверхности горизонтальными плоскостями уровня, то линии сечения будут простыми для построения линиями: для конуса - окружности, для цилиндра - образующие.

Сначала определим опорные точки. Это точки 1 и 2. Они определяются на пересечении очерковых образующих конуса с фронтальной проекцией цилиндра.

Боковая поверхность цилиндра является фронтально проецирующей.

Для нахождения промежуточных точек вводят ряд вспомогательных секущих горизонтальных плоскостей уровня ∑ ¹-∑ ⁵ Точки 3 и 4, определённые введением плоскости ∑ ², проходящей через ось цилиндра, являются точками границы видимости на горизонтальной проекции сечения. Полученные точки плавно соединяются с учётом видимости.

Пример 9. Определить линию пересечения вертикального it горизонтального конусов (рис. 6.12).

Решение. В данном случае целесообразно использовать метод секущих сфер, так как оси конусов пересекаются и параллельны фронтальной плоскости проекций. Первоначально определяем опорные (характерные) точки на пресечении очерковых образующих - точки 1 и 2. Для определения точек перехода через границу видимости вводим горизонтальную плоскость уровня ∑. Она пересекает вертикальный конус по окружности, а горизонтальный - по очерковым образующим. На их пересечении определяем точки 3 и 4.

Для нахождения промежуточных точек используем секущие сферы. Минимальная сфера радиуса R_min вписывается в больший конус. Оба конуса пересекаются сферой по окружностям, которые проецируются на фронтальную плоскость в виде прямых линий. На пересечении этих линий определяем точки 5 и 6. Далее вводим сферу большего радиуса, определяем точки 7 и 8. Полученные точки переносим на горизонтальную проекцию и плавно соединяем с учётом видимости.

Вопросы и задания для самоконтроля

1. Какая поверхность называется многогранником?

2. Перечислите правильные многогранники.

3. Что такое развёртка многогранника и какие способы её по
строения существуют?

4. Что называется каркасом поверхности?

5. Как определяют проекции точки, принадлежащей поверх-
ности вращения?

6. При каком расположении секущей плоскости в сечении ко-
нуса получаются окружность, парабола, эллипс и гипербола?

7. В чём сущность способов секущих плоскостей и секущих
сфер при определении линии пересечения поверхностей враще-
ния?

8.Определите линию пересечения двух конусов с вертикальными осями вращения (конусы задайте самостоятельно).

Рис 3.10. Следы прямой

Из этого следуют правила построения следов прямой:

1. Для построения проекций горизонтального следа

необходимо продолжить ее фронтальную проекцию до

пересечения с осью х (определяется проекция М₂) и из этой точки

восставить перпендикуляр к оси х до пересечения с

горизонтальной проекцией прямой (определяется проекция M ₁ = М).

2. Для построения проекций фронтального следа необходимо
продолжить ее горизонтальную проекцию до пересечения с осью
х (определяется точка N ₁ ) и из этой точки восставить
перпендикуляр к оси х до пересечения с фронтальной проекцией
прямой (определяется точка N₂ ≡ N).

3. Для построения проекций профильного следа необходимо
продолжить ее фронтальную проекцию до пересечения с осью z
(определяется точка Р₂) и из этой точки восставить
перпендикуляр к оси z до пересечения с профильной проекцией
прямой (определяется точка P₃≡ P). Горизонтальная проекция Р₁
определяется пересечением горизонтальной проекции прямой с
осью у.

3.5. Взаимное расположение прямых

Две прямые в пространстве могут занимать различное положение друг относительно друга: пересекаться, быть параллельными и скрещиваться.

1. Пересекающиеся прямые (рис. 3.11) имеют общую точку,
проекции которой К₁ и K₂ расположены на одной линии связи.

2. Параллельные прямые пересекаются в несобственной точке.
I la эпюре одноименные проекции параллельных прямых
параллельны, т. е. если а || b то а₁ || b ₁, а₂ || b _2, а₃ || b ₃ (рис. 3.12).

Для прямых общего положения их параллельность определяется двумя проекциями. Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, горизонтальные и фронтальные проекции профильных прямых всегда параллельны. Для оценки взаимного положения прямых следует построить их проекции на П3. В данном примере прямые АВ и CD параллельны.

ВВЕДЕНИЕ

Учебное пособие предназначено для студентов технических вузов и курсантов военных инженерных институтов.

СПОСОБЫ ПРОЕЦИРОВАНИЯ 1.1. Общие понятия метода проецирования

Операция проецирования является основой построения любого изображения.

Метод проекций заключается в проецировании каждой точки геометрического объекта на плоскость.

проецирование.

12 3 4 5 6 7 8 9 10 Следующая ⇒