
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Прямая линия, перпендикулярная плоскости
Прямая линия перпендикулярна плоскости, если она перпен-дикулярна любым двум пересекающимся прямым плоскости. Однако распознать перпендикулярность прямой линии и плос- кости в общем случае сложно, так как прямой угол проецируется на плоскость проекции в натуральную величину, когда одна из его сторон параллельна данной плоскости проекции. Следовательно, если на некоторой плоскости Z (рис. 4.19) провести две пересекающиеся прямые, одна из которых горизонталь h || П1, а другая — фронталь f || П2, то перпендикулярная к плоскости ∑ прямая а 53
проецируется на плоскость П1, перпендикулярно h1, а плоскость перпендикулярна f2. Итак, если прямая линия перпендикулярна к плоскости, то её горизонтальная проекция перпендикулярна горизонтальной про-екции горизонтали, а её фронтальная проекция - перпендикулярна фронтальной проекции фронтали, а также к одноимённым Следам. На рис. 4.19 рассмотрены случаи построения перпендикуляра из точки К к треугольнику ABC и к плоскости Z, заданной следа-ми. Если плоскости заданы не следами, то первоначально всегда Требуется определить горизонталь и фронталь в плоскости.
4.5.6. Взаимно перпендикулярные плоскости I Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Для построения плоскости, перпендикулярной к данной плоскости, достаточно определить прямую линию, ей перпендикуляр-ную. Через перпендикуляр к плоскости можно провести множе- ство плоскостей, перпендикулярных данной плоскости (рис. 4.20а).
Рис. 4.20а. Взаимно перпендикулярные плоскости Рис. 4.19. Прямая линия, перпендикулярная плоскости 54 55 Рассмотрим построение одной из плоскостей, перпендикулярной данной плоскости (с ∩ d ) (рис. 4.206).
4. Какие прямые линии в плоскости называются главными и 5. Сформулируйте условие параллельности прямой линии и 6. В каких случаях прямой угол между прямой линией и плос 7. В каких случаях плоскости пересекаются по линиям частно- а) прямыми уровня; б) проецирующими прямыми? 8. Определите линию пересечения двух плоскостей, заданных 9. Определите точку пересечения прямой общего положения L с плоскостью Z общего положения. Рис. 4.206. Взаимно перпендикулярные плоскости Определим горизонталь h и фронталь f данной плоскости. Из произвольной точки К восставим перпендикуляр а: на горизонтальной проекции a 1 ┴ h 1 а на фронтальной проекции a 1 ┴ f1. Дополним прямую а до плоскости, пересекающейся с ней произвольной прямой b. Плоскость (а ∩ b) перпендикулярна плоскости ( c ∩ b). Вопросы н задания для самоконтроля 1 Какими способами можно задать плоскость на чертеже? 2. Как можно перейти от любого способа задания плоскости к способу задания её следами? З.При каких условиях точка и прямая принадлежат плоскости? 56 57 СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ Преобразование проекций используется для наиболее выгодного изображения геометрических фигур при их исследовании и для решения метрических и позиционных задач. После преобразования чертежа объекты занимают частное положение относительно плоскостей проекций. Существует несколько способов преобразования проекций: - способ замены плоскостей проекций; - способ вращения вокруг проецирующих прямых и прямых уровня; - способ плоскопараллельного перемещения. Принципиальное отличие первого способа (замены плоскостей проекций) от других заключается в том, что объект не меняет своего положения в пространстве, а вводятся новые дополнительные плоскости проекций. При использовании способов вращения и плоскопараллельного перемещения система плоскостей остаётся неизменной, а объект перемещается относительно системы плоскостей. 5.1. Способ замены плоскостей проекций Сущность способа замены плоскостей рассмотрим на примере. На рис. 5.1 дана точка А в системе плоскостей проекций П1 / П2. Заменим одну из них, например П2, другой вертикальной плоскостью П4 ┴ П1, т.е. перейдём к новой системе плоскостей проекций П4 / П1. Определим новую фронтальную проекцию точки A 4, используя для этого неизменность координаты Z точки А, так как горизонтальная плоскость проекций П1 является общей для исходной и новой систем. На эпюре из горизонтальной проекции А1 проведём линию связи, перпендикулярную к новой оси, Х14 и отложим координату Z точки А. 58
Рис. 5.1. Способ замены плоскостей проекций Способом замены плоскостей определяют натуральную вели-чину прямой и плоскости, определяют расстояние между прямыми плоскостями и т.д. При решении задач приходится менять последовательно либо одну, либо две плоскости проекций так, 59 чтобы геометрические объекты оказались в частном положении относительно новой системы. Рассмотрим задачи на преобразование прямой и плоскости. ПРИМЕР. Дана прямая АВ общего положения (рис. 5.2). Преобразовать прямую АВ в проецирующую прямую.
лнрно прямой АВ, новая ось проекций Х45┴ A 4 B 4. Построим покую горизонтальную проекцию А5В5, отложив неизменную координату Y. Прямая АВ обращается в точку А5 ≡ В5 и является гори-юнтально проецирующей прямой в новой системе плоскостей П4/П5.
XiE |
 Пример 2. Даны две параллельные прямые линии АВ и CD (рис. 5.3). Определить расстояние между ними.
Пример 2. Даны две параллельные прямые линии АВ и CD (рис. 5.3). Определить расстояние между ними.
| П |
%
Рис. 5.2
Решение. Прямую общего положения можно преобразовать в проецирующую прямую только двумя последовательными заменами плоскостей проекций, так как плоскость проекций, перпендикулярная к прямой общего положения, не будет перпендикулярна ни к П1 ни к П2. Первоначально заменим плоскость проекций П2 на П4 (┴ П1) параллельно прямой АВ, новая ось проекций х4||А1В1. Построим новую фронтальную проекцию А4В4, отложив неизменную координату Z. Прямая АВ преобразована в новой системе П1/П4 во фронталь, А4В4 - натуральная величина отрезка прямой, а угол а - угол наклона прямой к плоскости проекций П1. Затем заменим плоскость проекций П1 на П5 (┴ П4) перпендику-
60
Рис. 5.3
Решение. Чтобы определить расстояние между параллельными прямыми, необходимо преобразовать их в проецирующие прямые. Этого можно добиться двумя последовательными заменами плоскостей проекций. Первая замена плоскости проекций П1| на П5 — параллельно данным прямым, новая ось проекций Х25|| С2D2 ||A 2 B 2. Прямые АВ и CD преобразованы в новой системе плоскостей проекций П2/П5 в горизонтали. Вторая замена плоскости проекций П2 на П4 - перпендикулярно прямым АВ и CD, новая ось проекций Х45 ┴ C 5 D 5 ┴ (А5В5)- На новую фрон-
61
тальную плоскость П4 прямые АВ и CD проецируются в точки А4 = В4, С4 = D4. Измеряем расстояние между точками.
Пример 3. Дана плоскость, заданная треугольником ABC общего положения (рис. 5.4). Определить натуральную величину треугольника ABC.
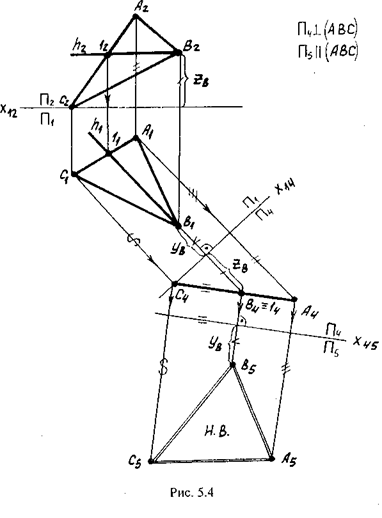
Решение. Чтобы определить натуральную величину плоскости, необходимо расположить её параллельно плоскости проекций. Плоскость общего положения невозможно сразу преобразовать в плоскость уровня, так как параллельная ей новая плоскость проекции не будет перпендикулярна ни к П1, ни к П2. По-чтому необходимо выполнить две последовательные замены плоскостей проекций, преобразовав данную плоскость сначала в проецирующую, а затем в плоскость уровня.
Заменим плоскость проекций П2 на П4 перпендикулярно треугольнику ABC. Чтобы определить направление П4, проведём в треугольнике ABC горизонталь h. Новая плоскость проекций П4 будет перпендикулярна горизонтали, новая ось проекций Х14 ┴ h 1. На линии связи откладываем неизменные координаты ZA, Z В, Z С. Новая фронтальная проекция А4 В4 С4 в системе плоскостей П1/П4 представляет собой прямую линию, плоскость ( ABC ) преобразо-вана во фронтально проецирующую.
Затем заменим плоскость проекций П1 на плоскость П5 параллельно треугольнику ABC, новая ось проекций Х45 || А4, В4, С4 , неизменной остаётся координата Y. В новой системе плоскостей П4/П5 треугольник ABC является горизонтальной плоскостью уровня. Новая горизонтальная проекция A 5 B 5 C 5 - натуральная величина треугольника АВС.
5.2. Способ вращения
Суть способа вращения состоит в том, что геометрический объект вращают в пространстве вокруг выбранной оси i до тре-буемого положения относительно плоскостей проекций. Траектории движения точек объекта являются дугами окружностей, центр которых находится на оси вращения.
62
63
|
|
Последнее изменение этой страницы: 2019-05-06; Просмотров: 59; Нарушение авторского права страницы