Линейные однородные и неоднородные уравнения с постоянными
Коэффициентами, метод вариации постоянной
Линейное однородное уравнение 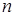 -го порядка с постоянными коэффициентами имеет вид
-го порядка с постоянными коэффициентами имеет вид
 ,
,
где  вещественные постоянные числа. Общим решением уравнения будет
вещественные постоянные числа. Общим решением уравнения будет  , где
, где 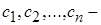 произвольные постоянные числа. Для нахождения линейно независимых частных решений
произвольные постоянные числа. Для нахождения линейно независимых частных решений  рассматриваемого уравнения используется метод Эйлера. Для этого составляем уравнение
рассматриваемого уравнения используется метод Эйлера. Для этого составляем уравнение  , которое называется характеристическим. Решив его, получим четыре случая.
, которое называется характеристическим. Решив его, получим четыре случая.
1) Корни  вещественные, не равные друг другу числа. Тогда
вещественные, не равные друг другу числа. Тогда  ,
,  ,...,
,...,  .
.
2) Корни  не равны между собой, но среди них есть комплексно сопряженные корни. Каждой паре
не равны между собой, но среди них есть комплексно сопряженные корни. Каждой паре  соответствуют два частных решения
соответствуют два частных решения  ,
,  .
.
3) Корни  все вещественные, но среди них некоторые совпадают, например,
все вещественные, но среди них некоторые совпадают, например,  (в этом случае говорят, что корень
(в этом случае говорят, что корень  имеет кратность
имеет кратность 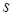 ). Совпадающим
). Совпадающим 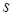 корням соответствуют следующие частные решения:
корням соответствуют следующие частные решения:  .
.
4) Корни  содержат
содержат 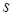 равных комплексно сопряженных пар
равных комплексно сопряженных пар  , тогда им соответствуют
, тогда им соответствуют  частных решения:
частных решения:
 ,
,
 .
.
Линейное неоднородное уравнение 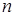 -го порядка с постоянными коэффициентами имеет вид
-го порядка с постоянными коэффициентами имеет вид
 ,
,
где  вещественные постоянные числа. Общим решением данного уравнения является сумма общего решения
вещественные постоянные числа. Общим решением данного уравнения является сумма общего решения  соответствующего однородного уравнения и какого-либо частного решения
соответствующего однородного уравнения и какого-либо частного решения  неоднородного уравнения:
неоднородного уравнения: 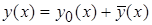 . Для нахождения частного решения можно воспользоваться методом Лагранжа (метод вариации постоянной). Для этого вначале находят общее решение соответствующего однородного уравнения:
. Для нахождения частного решения можно воспользоваться методом Лагранжа (метод вариации постоянной). Для этого вначале находят общее решение соответствующего однородного уравнения: 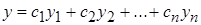 . Затем предполагают, что
. Затем предполагают, что  являются функциями от
являются функциями от 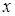 , и ищут общее решение неоднородного уравнения в виде
, и ищут общее решение неоднородного уравнения в виде  , где производные неизвестных функций
, где производные неизвестных функций  находят из системы уравнений
находят из системы уравнений

Решив систему, мы найдем  . Проинтегрировав последние уравнения, определим неизвестные функции
. Проинтегрировав последние уравнения, определим неизвестные функции 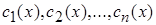 , тем самым найдем общее решение линейного неоднородного уравнения.
, тем самым найдем общее решение линейного неоднородного уравнения.
Примеры решения задач
1. Найти общее решение уравнения
 .
.
Решение. Составим характеристическое уравнение  , его корни
, его корни  , отсюда фундаментальная система решений
, отсюда фундаментальная система решений  ,
,  . Следовательно, общее решение имеет вид:
. Следовательно, общее решение имеет вид:  .
.
2. Найти частное решение уравнения
 ,
,  .
.
Решение. Найдем вначале общее решение, для этого составим характеристическое уравнение 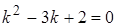 , его корни
, его корни 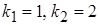 , отсюда фундаментальная система решений
, отсюда фундаментальная система решений  ,
,  . Следовательно, общее решение имеет вид:
. Следовательно, общее решение имеет вид:  .
.
Теперь определим произвольные постоянные  по заданным начальным условиям. Найдем производную
по заданным начальным условиям. Найдем производную  . Подставив начальные условия в
. Подставив начальные условия в  и
и  , получим систему уравнений
, получим систему уравнений

решением которой является 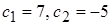 . Подставив найденные значения постоянных в общее решение, найдем частное решение:
. Подставив найденные значения постоянных в общее решение, найдем частное решение:  .
.
3. Найти общее решение уравнения
 .
.
Решение. Характеристическое уравнение  можно разложить так:
можно разложить так:

 .
.
Найдем корни  . Первому корню соответствует частное решение
. Первому корню соответствует частное решение  . Второй корень двукратный, то есть кратности 2, поэтому ему соответствуют два частных решения:
. Второй корень двукратный, то есть кратности 2, поэтому ему соответствуют два частных решения:  .
.
Таким образом, общее решение исходного уравнения:
 .
.
4. Найти общее решение уравнения
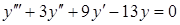 .
.
Решение. Характеристическое уравнение 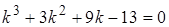 поделим уголком на
поделим уголком на  , получим
, получим  . Следовательно, уравнение
. Следовательно, уравнение
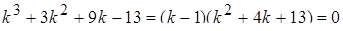 ,
,
имеет корни  . Первому вещественному корню соответствует частное решение
. Первому вещественному корню соответствует частное решение  , а паре комплексно сопряженных корней частные решения
, а паре комплексно сопряженных корней частные решения  . Общее решение запишется в виде:
. Общее решение запишется в виде: 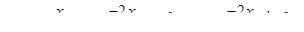 .
.
5. Найти общее решение уравнения
 .
.
Решение. Характеристическое уравнение  разложим на множители
разложим на множители


и найдем корни  . Первые два вещественных корня совпадают, их частные решения имею вид
. Первые два вещественных корня совпадают, их частные решения имею вид  . Следующие корни комплексно сопряженные, причем их реальная часть
. Следующие корни комплексно сопряженные, причем их реальная часть  , отсюда их частные решения
, отсюда их частные решения  . Таким образом, имеем общее решение заданного уравнения:
. Таким образом, имеем общее решение заданного уравнения:  .
.
6. Найти общее решение уравнения
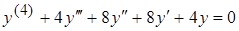 .
.
Решение. Характеристическое уравнение  , которое можно переписать в виде
, которое можно переписать в виде  имеет две равные комплексно-сопряженные пары корней
имеет две равные комплексно-сопряженные пары корней  . Тогда, получим четыре частных решения:
. Тогда, получим четыре частных решения:

 .
.
Отсюда, общее решение запишется как

7. Найти частное решение уравнения
 ,
, 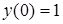 ,
, 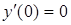 .
.
Решение. Характеристическое уравнение  соответствующего однородного уравнения
соответствующего однородного уравнения  имеет корни
имеет корни  , следовательно, общее решение однородного уравнения:
, следовательно, общее решение однородного уравнения:  .
.
Ищем решение неоднородного уравнения в виде
 .
.
Уравнения на неизвестные функции  следующие:
следующие:
 ,
,
 .
.
Выразив  из первого уравнения и подставив во второе, после несложных преобразований найдем
из первого уравнения и подставив во второе, после несложных преобразований найдем  tg x. Подставив найденное
tg x. Подставив найденное  в первое уравнение и выразив оттуда
в первое уравнение и выразив оттуда  , определим
, определим 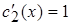 . После интегрирования найдем
. После интегрирования найдем
 ,
,  ,
,
где 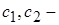 произвольные постоянные числа. Запишем общее решение заданного неоднородного уравнения:
произвольные постоянные числа. Запишем общее решение заданного неоднородного уравнения:
 .
.
Применив начальное условие 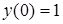 , получим
, получим
 ,
,
отсюда  . Вычислив производную
. Вычислив производную
 ,
,
с учетом второго условия 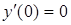 найдем
найдем
 ,
,
отсюда  . Следовательно, частное решение исходного уравнения имеет вид:
. Следовательно, частное решение исходного уравнения имеет вид:  .
.
8. Найти общее решение уравнения
 .
.
Решение. Характеристическое уравнение  соответствующего однородного уравнения имеет корни
соответствующего однородного уравнения имеет корни  , следовательно, общее решение однородного уравнения:
, следовательно, общее решение однородного уравнения:  .
.
Ищем решение неоднородного уравнения в виде
 .
.
Система на функции  имеет вид:
имеет вид:

Определитель этой системы не равен нулю. Решив методом Крамера, найдем
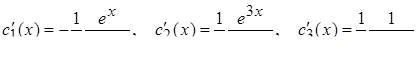 .
.
Интегрируя последние равенства, получим
 ,
,

 ,
,
 ,
,
где 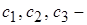 произвольные постоянные.
произвольные постоянные.
Итак, общее решение исходного неоднородного уравнения:

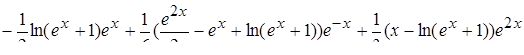 .
.
Задачи для самостоятельного решения
1.  . Ответ:
. Ответ: 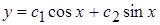 .
.
2. 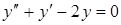 . Ответ:
. Ответ: 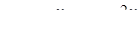 .
.
3.  . Ответ:
. Ответ:  .
.
4.  . Ответ:
. Ответ: 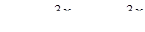 .
.
5. 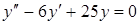 . Ответ:
. Ответ:  .
.
6.  . Ответ:
. Ответ:  .
.
7. 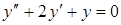 . Ответ:
. Ответ:  .
.
8.  . Ответ:
. Ответ:  .
.
9.  . Ответ:
. Ответ:  .
.
10.  . Ответ:
. Ответ:  .
.
11.  . Ответ:
. Ответ:  .
.
12.  . Ответ:
. Ответ:  .
.
13.  . Ответ:
. Ответ:  .
.
14.  . Ответ:
. Ответ:  .
.
15.  .
.
Ответ:  .
.
16.  . Ответ:
. Ответ:  .
.
17.  . Ответ:
. Ответ:  .
.
18.  . Ответ:
. Ответ:  .
.
19. 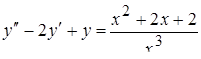 . Ответ:
. Ответ:  .
.
20.  . Ответ:
. Ответ:  .
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 16

