Линейные неоднородные уравнения с постоянными коэффициентами
С правой частью специального вида
Напомним, что линейное неоднородное уравнение 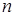 -го порядка с постоянными коэффициентами имеет вид
-го порядка с постоянными коэффициентами имеет вид
 ,
,
где коэффициенты  вещественные постоянные числа.
вещественные постоянные числа.
Общим решением такого уравнения является сумма общего решения  соответствующего однородного уравнения и какого-либо частного решения
соответствующего однородного уравнения и какого-либо частного решения  неоднородного уравнения:
неоднородного уравнения: 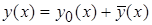 . Иногда частное решение удается найти в зависимости от правой части неоднородного уравнения, то есть от вида функции
. Иногда частное решение удается найти в зависимости от правой части неоднородного уравнения, то есть от вида функции  . Рассмотрим разные случаи.
. Рассмотрим разные случаи.
1) Если  полином
полином  -ой степени, и число нуль не является корнем характеристического уравнения соответствующего однородного уравнения, то частное решение ищем в виде
-ой степени, и число нуль не является корнем характеристического уравнения соответствующего однородного уравнения, то частное решение ищем в виде  , где
, где 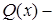 полином
полином  -ой степени, но с неопределенными коэффициентами. Для нахождения неизвестных коэффициентов надо воспользоваться методом неопределенных коэффициентов. Если нуль является корнем характеристического уравнения кратности
-ой степени, но с неопределенными коэффициентами. Для нахождения неизвестных коэффициентов надо воспользоваться методом неопределенных коэффициентов. Если нуль является корнем характеристического уравнения кратности 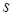 , тогда частное решение ищем в виде
, тогда частное решение ищем в виде  .
.
2) Если  и число
и число  не является корнем характеристического уравнения соответствующего однородного уравнения, то частное решение ищем в виде
не является корнем характеристического уравнения соответствующего однородного уравнения, то частное решение ищем в виде  . Здесь полином
. Здесь полином  с неопределенными коэффициентами, причем той же степени, что и полином
с неопределенными коэффициентами, причем той же степени, что и полином  . Если
. Если  является корнем характеристического уравнения кратности
является корнем характеристического уравнения кратности 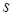 , тогда частное решение ищем в виде
, тогда частное решение ищем в виде  .
.
3) Если  , где
, где 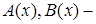 полиномы, их степени могут не совпадать, и комплексное число
полиномы, их степени могут не совпадать, и комплексное число  не является корнем характеристического уравнения, то частное решение ищем в виде
не является корнем характеристического уравнения, то частное решение ищем в виде  , здесь степень полиномов
, здесь степень полиномов  с неопределенными коэффициентами совпадает с наибольшей степенью полиномов
с неопределенными коэффициентами совпадает с наибольшей степенью полиномов  . Если комплексное число
. Если комплексное число  является корнем характеристического уравнения кратности
является корнем характеристического уравнения кратности 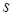 , то частное решение ищем в виде
, то частное решение ищем в виде  .
.
Примеры решения задач
1. Найти общее решение уравнения
 .
.
Решение. Составим однородное уравнение  . Его характеристическое уравнение
. Его характеристическое уравнение 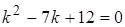 имеет корни
имеет корни  , отсюда, получим общее решение однородного уравнения:
, отсюда, получим общее решение однородного уравнения:  .
.
Теперь рассмотрим правую часть заданного неоднородного уравнения. В правой части стоит число 5, которое надо рассматривать как полином нулевой степени. Так как число нуль не является корнем характеристического уравнения, то частное решение неоднородного уравнения ищем в виде  , где A является произвольным полиномом нулевой степени, то есть произвольной постоянной. Для ее нахождения, надо
, где A является произвольным полиномом нулевой степени, то есть произвольной постоянной. Для ее нахождения, надо  подставить в исходное неоднородное уравнение:
подставить в исходное неоднородное уравнение:  . Отсюда видно, что
. Отсюда видно, что 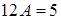 , или
, или  , следовательно,
, следовательно,  .
.
Итак, общее решение заданного уравнения имеет вид
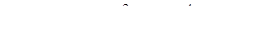 .
.
2. Найти общее решение уравнения
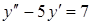 .
.
Решение. Для соответствующего однородного уравнения  характеристическое уравнение
характеристическое уравнение  имеет корни
имеет корни  , отсюда, получим общее решение однородного уравнения:
, отсюда, получим общее решение однородного уравнения:  .
.
Правая часть неоднородного уравнения представляет собой полином нулевой степени, при этом число нуль является корнем характеристического уравнения кратности 1, поэтому частное решение ищем в виде  . Подставляем в исходное неоднородное уравнение:
. Подставляем в исходное неоднородное уравнение:  ,
,  . Отсюда,
. Отсюда, 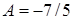 , тогда
, тогда  .
.
Таким образом, общее решение:  .
.
3. Найти общее решение уравнения
 .
.
Решение. Характеристическое уравнение  однородного уравнения
однородного уравнения  имеет корни
имеет корни  , следовательно,
, следовательно,  .
.
В правой части неоднородного уравнения стоит полином второго порядка. Число нуль является корнем кратности 2 характеристического уравнения. Поэтому частное решение ищем в виде  , где в скобках стоит полином второй степени с неопределенными коэффициентами. Для их определения надо
, где в скобках стоит полином второй степени с неопределенными коэффициентами. Для их определения надо 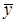 подставить в исходное уравнение. Предварительно вычислим производные:
подставить в исходное уравнение. Предварительно вычислим производные:
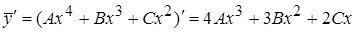 ,
,
 ,
,
 ,
,
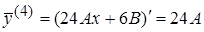 .
.
Подставив производные в неоднородное уравнение, найдем
 .
.
Приравняв коэффициенты при одинаковых степенях x в левой и правой частях последнего равенства, получим систему алгебраических уравнений для определения чисел A, B, C:

откуда 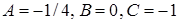 . Тогда, получим частное решение в виде
. Тогда, получим частное решение в виде
 .
.
Общим решением заданного уравнения является функция
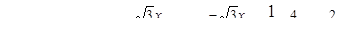 .
.
4. Найти общее решение уравнения
 .
.
Решение. Составим однородное уравнение  . Его характеристическое уравнение
. Его характеристическое уравнение  имеет корни
имеет корни  . Следовательно, получим общее решение однородного уравнения в виде
. Следовательно, получим общее решение однородного уравнения в виде  .
.
Правая часть заданного уравнения состоит из суммы трех функций  . Поэтому вначале мы найдем частные решения уравнений:
. Поэтому вначале мы найдем частные решения уравнений:
1)  , 2)
, 2)  , 3)
, 3)  .
.
Первое уравнение описано в пункте 2). Сравнив  с нашей правой частью
с нашей правой частью 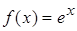 , найдем
, найдем 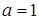 и
и  полином нулевой степени. Число
полином нулевой степени. Число 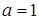 совпадает с одним из корней
совпадает с одним из корней  , отсюда частное решение первого уравнения ищем в виде
, отсюда частное решение первого уравнения ищем в виде  , где
, где  полином нулевой степени, то есть число, которое надо определить. Для этого вычислим производные
полином нулевой степени, то есть число, которое надо определить. Для этого вычислим производные  ,
,  и подставим их в первое уравнение
и подставим их в первое уравнение
 , или
, или  ,
,
отсюда 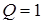 , следовательно,
, следовательно,  .
.
Второе уравнение с правой частью  описано в пункте 2). Число
описано в пункте 2). Число  не совпадает ни с одним из корней характеристического уравнения, поэтому частное решение второго уравнения ищем в виде
не совпадает ни с одним из корней характеристического уравнения, поэтому частное решение второго уравнения ищем в виде  . Вычислив производные и подставив их во второе уравнение, найдем
. Вычислив производные и подставив их во второе уравнение, найдем 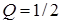 , тогда
, тогда  .
.
Третье уравнение описано в пункте 1). Сравнив  с нашей правой частью
с нашей правой частью  , найдем
, найдем 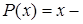 полином первой степени. Также нуль является корнем характеристического уравнения кратности 1, поэтому частное решение ищем в виде
полином первой степени. Также нуль является корнем характеристического уравнения кратности 1, поэтому частное решение ищем в виде 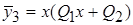 , где
, где 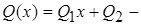 полином первой степени с неопределенными коэффициентами
полином первой степени с неопределенными коэффициентами  . Вычислив производные
. Вычислив производные  ,
,  и подставив их в третье уравнение, получим
и подставив их в третье уравнение, получим
 .
.
Приравняв коэффициенты при одинаковых степенях 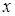 в левой и правой частях полученного равенства, найдем систему алгебраических уравнений
в левой и правой частях полученного равенства, найдем систему алгебраических уравнений

решением которой является  ,
,  , отсюда
, отсюда  .
.
Итак, частным решением исходного уравнения будет
 ,
,
а общим решением  .
.
5. Найти общее решение уравнения
 .
.
Решение. Запишем однородное уравнение  . Его характеристическое уравнение
. Его характеристическое уравнение  имеет корни
имеет корни  . Следовательно, общее решение однородного уравнения:
. Следовательно, общее решение однородного уравнения:
 .
.
Правая часть заданного неоднородного уравнения имеет вид  , где
, где  . Заметим, что число а не является корнем характеристического уравнения. Поэтому частное решение ищем в виде
. Заметим, что число а не является корнем характеристического уравнения. Поэтому частное решение ищем в виде
 .
.
Подставив 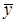 в неоднородное уравнение, найдем
в неоднородное уравнение, найдем
 .
.
Сравнивая коэффициенты при одинаковых степенях x, получим:
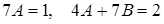 ,
,
отсюда  . Тогда
. Тогда  , следовательно, общее решение исходного уравнения запишется в виде
, следовательно, общее решение исходного уравнения запишется в виде
 .
.
6. Найти общее решение уравнения
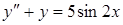 .
.
Решение. Характеристическое уравнение соответствующего однородного уравнения  имеет корни
имеет корни  , следовательно, общее решение однородного уравнения
, следовательно, общее решение однородного уравнения  .
.
Правая часть уравнения имеет вид  , где
, где  . Число
. Число  не является корнем характеристического уравнения и полиномы
не является корнем характеристического уравнения и полиномы  являются полиномами нулевой степени. Поэтому частное решение ищем в виде
являются полиномами нулевой степени. Поэтому частное решение ищем в виде
 .
.
Подставив 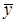 в заданное неоднородное уравнение, найдем
в заданное неоднородное уравнение, найдем
 .
.
Приравнивая коэффициенты в левой и правой частях равенства при 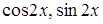 , получим
, получим
 .
.
Значит, 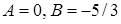 . Поэтому
. Поэтому 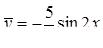 , следовательно, общее решение исходного уравнения:
, следовательно, общее решение исходного уравнения:  .
.
7. Найти общее решение уравнения
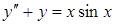 .
.
Решение. Характеристическое уравнение соответствующего однородного уравнения  имеет корни
имеет корни  , следовательно, общее решение однородного уравнения
, следовательно, общее решение однородного уравнения  .
.
Правая часть заданного уравнения представляет собой функцию вида  , где
, где  . Видно, что число
. Видно, что число  совпадает с числом
совпадает с числом 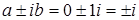 , то есть
, то есть  является корнем характеристического уравнения кратности 1. Полином
является корнем характеристического уравнения кратности 1. Полином  есть полином первой степени. Таким образом, ищем частное решение в виде
есть полином первой степени. Таким образом, ищем частное решение в виде
 ,
,
где  неопределенные коэффициенты. Дифференцируем частное решение два раза и результат подставляем в заданное неоднородное уравнение. В полученном равенстве, приравняв коэффициенты в левой и правой частях при
неопределенные коэффициенты. Дифференцируем частное решение два раза и результат подставляем в заданное неоднородное уравнение. В полученном равенстве, приравняв коэффициенты в левой и правой частях при  , получим систему алгебраических уравнений
, получим систему алгебраических уравнений
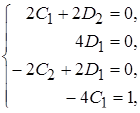
решениями которых являются  , отсюда
, отсюда
 .
.
Тогда общим решением заданного уравнения будет
 .
.
Задачи для самостоятельного решения
1.  . Ответ:
. Ответ:  .
.
2.  . Ответ:
. Ответ:  .
.
3.  . Ответ:
. Ответ:  .
.
4.  . Ответ:
. Ответ: 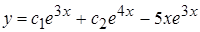 .
.
5.  . Ответ:
. Ответ:  .
.
6.  . Ответ:
. Ответ:  .
.
7. 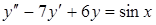 . Ответ:
. Ответ:  .
.
8. 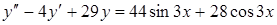 .
.
Ответ: 
 .
.
9. 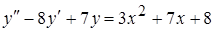 . Ответ:
. Ответ: 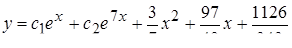 .
.
10.  . Ответ:
. Ответ:  .
.
11.  .
.
Ответ: 
 .
.
12.  . Ответ:
. Ответ:  .
.
13.  . Ответ:
. Ответ:  .
.
14.  .
.
Ответ: 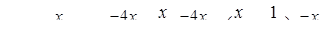 .
.
15.  .
.
Ответ: 
 .
.
16.  . Ответ:
. Ответ:  .
.
17.  . Ответ:
. Ответ: 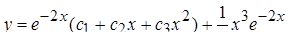 .
.
18.  . Ответ:
. Ответ: 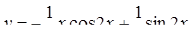 .
.
19.  . Ответ:
. Ответ:  chx.
chx.
20.  . Ответ:
. Ответ:  .
.

