
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Базис. Разложение вектора по базису.
10 Базис. Рассмотрим в пространстве R3систему декартовых прямоугольных координат. Тройку векторов, 1) Вектор 2) Векторы 3) Векторы называют координатным базисом. Любой вектор в пространстве может быть выражен через векторы
20Пусть вектор, задан координатами начала и конца А(х1, у1, z1) и В(х2, у2, z2). Проекции вектора
Проекции X, Y, Z вектора
Формула:
выражает длину вектора
30 Пусть
причём
Пример2. Пусть (см.рис.) М- середина ВС и N- середина AC. Определить векторы Решение. Имеем
Следовательно,
Ответ:
Пример3 . Даны точки А(1; 2; 3) и В(3; -4; 6). Найти длину вектора Решение. По формулам (2) имеем: Х=3-1=2
Z=6-3=3 Следовательно, Далее по формуле (4) и (5) получим:
Пример 4. Радиус вектора точки М составляет с осью ох угол 450 с осью оу угол 600. Длина его r=6. Определить координаты точки М, если её координата z- отрицательна, и выразить вектор Решение. По формулам (5) имеем:
т.е.
3 . Скалярное произведение. 10 Скалярным произведением двух ненулевых векторов Скалярное произведение векторов
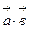 = =  , ,
Где 20 Свойства скалярного произведения: 1) 2) 3) 4) Если а 1) Если 2) Для базисных векторов
30 Если векторы
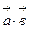 = = 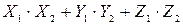 . .
40 Угол между векторами:
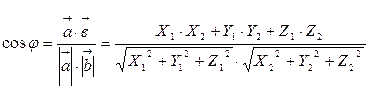
Условие параллельности векторов
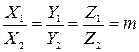 , ,
т.е.
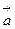 и и 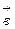 есть: есть: 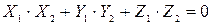
Пример 5. Определить угол между векторами Решение.
Пример 6. Определить угол между векторами Решение .
Пример 7. Определить углы треугольника А(2; -1; 3), В(1; 1; 1) и С(0; 0; 5). Решение. По формуле (2) найдём координаты векторов:
Скалярное произведение из (8):
Следовательно, векторы Далее находим координаты вектора: По формуле (9): Следовательно,
Пример 8. Найти скалярное произведение векторов Решение.
Векторное произведение. 10 Векторным произведением вектора 1) длина вектора 2) Вектор 3) Векторы Векторное произведение обозначается
20 Свойства векторного произведения: 1) 2) 3) 4) 30 40 Выражение векторного произведения через координаты сомножителей:
 = = 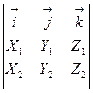
Эту формулу с помощью определителей второго порядка можно записать в виде:
 = = 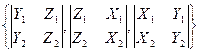
50 Площадь параллелограмма построенного на векторах S= И площадь треугольника построенного на векторах S=
Пример 8. Даны векторы Найти: 1) Решение. 1) Находим векторное произведение
2) Найдём координаты вектора
Ответ:
Пример 9. Вычислить площадь параллелограмма, построенного на векторах Решение. Находим векторное произведение
Пример 10. Вычислить площадь треугольника с вершинами А(7; 3; 4), В(1; 0; 6) и С(4; 5; -2). Решение. находим векторы
Площадь треугольника АВС равна половине площади параллелограмма построенного на векторах
Ответ: S=24, 5 кв.ед.
5.Смешанное произведение трех векторов . 10 Смешенным произведением векторов

20 Свойства смешанного произведения: 1) 2) Если два из трёх данных векторов равны или параллельны, то их смешанное произведение равно 0. 3)
30 Объём параллелепипеда, построенного на векторах
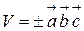
( + при правой тройке, - при левой) Объём пирамиды построенной на векторах

40 Если
Пример 11. Найти смешанное произведение векторов Решение. По формуле (15), находим:
Ответ: 4.
Пример 12. Найти объём треугольной пирамиды с вершинами А(0; 0; 1), В(2; 3; 5), C(6; 2; 3) и D(3; 7; 2). Решение. Найдём векторы
Найдём смешанное произведение этих векторов:
Так как объём пирамиды равен Ответ:
Пример 13. Даны радиус вектора трёх последовательных вершин параллелограмма ABCD: Решение.
Так как Решая систему
Получим x=7, y=7, z=7. Ответ. Пример 14. Установить, компланарны ли векторы Решение. Найдём смешанное произведение:
следовательно, векторы Контрольные вопросы. 1.Векторы. Линейные операции над векторами. 2.Базис. Разложение вектора по базису. 3.Скалярные произведения. 4.Векторные произведения. 5.Смешанное произведение двух векторов.
Задания. 1. Проверить векторные тождества 1)
2. В равнобедренной трапеции ОАСВ угол ВОА=600 , ОВ=ВС=СА=2, М и N- середины сторон ВС и АС. Выразить векторы 4. Вектор 5. Даны точки А(2; 2; 0) и В(0; -2; 5). Построить вектор 6. Даны векторы а) 7. Определить при каком значении m векторы 8. Даны точки А(3; 3; -2), В(0; -3; -4), С(0; -3; 0) и D(0; 2; -4). Построить векторы 9. Векторы 1) 11.Векторы 12.Даны векторы 14.Вычислить площадь параллелограмма построенного на векторах 15.Вычислить площадь параллелограмма, построенного на векторах: 16. Найти смешанное произведение векторов: a=i-j+k, в=i+j+k, c=2i+3j+4k. 17. Показать, что векторы: a=7i-3j+2k, в=3i-7j+8k, c=i-j-k - компланарны. 3) Вычислить объём треугольной пирамиды с вершинами А(0; 0; 1), В(2; 3; 5), С(6; 2; 3) и D(3; 7; 2). Найти длину высоты пирамиды, опущенной на грань BCD.
Тема 5. Популярное:
|
Последнее изменение этой страницы: 2016-03-17; Просмотров: 2122; Нарушение авторского права страницы