Касательная и нормаль к кривой.

Если кривая задана в декартовой системе координат уравнением

, то , где - угол между касательной к этой кривой в точке с абсциссой и положительным направлением оси .

Если кривая задана уравнением , то уравнения касательной и нормали к этой кривой в точке имеют соответственно вид:

, (1)

. (2)

Угол между двумя кривыми и в точке их пересечения определяется как угол между прямыми, касательными к этим кривым в точке их пересечения по формуле

, (3)

где угловые коэффициенты касательных к кривым в точке их пересечения и равны соответственно , .

Пример 1. Составить уравнение касательной и нормали к кривой в точке .

Решение. Подставляя в заданное уравнение параболы значение , находим ординату точки касания . Находим угловой коэффициент касательной, , следовательно, . Подставляя найденные значение в уравнение (1), имеем уравнение касательной , подставляя эти же значения в уравнение (2), получим уравнение нормали .

Пример 2. Найти углы под которыми пересекаются прямая и парабола .

Решение. Найдем точки пересечения кривых, решив систему уравнений

Отсюда имеем , . Далее, определим угловые коэффициенты касательных к параболе в точках и .Соответственно имеем , . Угловой коэффициент прямой во всех точках один и тот же и равен в нашем случае 2. Далее находим углы ,

Пример 3. Определить в каких точках заданной линии касательная к этой линии параллельна прямой и написать уравнение этой касательной

, .

Решение. Находим производную . Далее находим значение из уравнения . Имеем, .Значения функции при есть и . Отсюда имеем, и точки заданной линии в которых касательная к этой линии параллельна данной прямой . Найдем теперь уравнения этих касательных. Используя формулу (1), получим

-уравнение касательной в точке ,

-уравнение касательной в точке .

Контрольные вопросы.

1.Геометрический смысл производной.

2.Касательная и нормаль к кривой.

3.Угол между двумя кривыми.

4.Другие приложения производной.

Задания.

1.Найти углы, под которыми пересекаются эллипс и парабола

, .

2. Определить в каких точках заданной линии касательная к этой линии параллельна прямой и написать уравнение этой касательной

1) , ; 2) , ; 3) , .

3.Найти угол между кривой и прямой

Тема 14.

Интегральное исчисление.

Неопределенный интеграл.

Функция - называется первообразной для функции на промежутке , если в каждой точке этого промежутка выполняется равенство

или .

Если первообразная для функции , то множество , где произвольная постоянная, называется неопределённым интегралом от функции и обознается

При этом называется подынтегральной функцией.

Процесс отыскания первообразной называется интегрированием.

Свойства неопределённого интеграла:

1. ,

2. ,

3. ,

4. , где некоторая постоянная,

5. .

6. (Инвариантность формулы интегрирования) Если = , то и

= .

Пример 1. Найти первообразную функции .

Решение. Рассмотрим функцию => .

Следовательно, первообразная есть

Таблица основных интегралов:

1. ,

2. при ,

3. ,

4. , при и , и в частности ,

5. ,

6. ,

7. ,

8. ,

9. ,

10. ,

11. ,

12. .

Пример 2. Вычислить интеграл .

Решение.

Пример 3 . Вычислить интеграл .

Решение .

Замена переменной в неопределённом интеграле.

Пусть - первообразная для функции на некотором множестве . Если непрерывно дифференцируемая функция на некотором множестве , то

Пример 4. Вычислить интеграл .

Решение.

Пример 5. Вычислить

Пример 6. Вычислить

Интегрирование по частям.

Пусть и - некоторые непрерывно дифференцируемые функции на некотором множестве .

Формула интегрирования по частям:

Пример 7. Вычислить интеграл

Решение. Положим , откуда По формуле интегрирования по частям при , имеем

Пример 8 . Вычислить интеграл

Решение. Положим

Тогда

Поэтому по формуле интегрирования по частям

К последнему интегралу применяем ещё раз формулу интегрирования по частям, где и

Итак,

Контрольные вопросы.

1. Первообразная и неопределённый интеграл.

2. Методы интегрирования.

3. Основные свойства неопределённого интеграла.

4.Таблица основных интегралов.

5.Замена переменной в неопределённом интеграле.

6.Формула интегрирование по частям.

Задания.

1. Вычислить интегралы:

1) , 2) , 3) , 4) .

2.Решить заменой переменной:

1) 2) .

3.Решить рациональные дроби:

1) 2) ; 3) ; 4) .

3.Применяя формулу интегрирование по частям, найти интегралы:

1) 2) 3)

4) ; 5) 6) 7) ; 8) .

Тема 15

Определённый интеграл

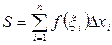Пусть функция определена на отрезке , . Разобьем этот отрезок на частичных отрезков точками . В каждом из полученных частичных отрезков выберем произвольную точку

Сумма

- называется интегральной суммой для функции

на отрезке .

Предел интегральной суммы

при , который не

зависит ни от способа разбиения

отрезка на частичные отрезки,

ни от выбора точек в них, называется

определенным интегралом

от функции на отрезке

и обозначается

Свойства определённого интеграла.

1. ,

2. ,

3. .

.Формула Ньютона- Лейбница.

Если функция непрерывна на отрезке и функция является некоторой ее первообразной на этом отрезке, то имеет место формула Ньютона-Лейбница

.

Пример 1. Вычислить интегралы

а)

б) .

Пример 2. Вычислить интеграл .

Решение. .

Пример 3. Вычислить интеграл ( заменой переменной).

2.Вычисление площадей плоских фигур.

Площадь криволинейной трапеции ограниченной линиями , , расположенной выше оси Ох ( ), равна:

.

Если криволинейная трапеция расположена ниже оси Ох ( ), то ее площадь может быть найдена по формуле

.

Пусть на отрезке заданны и непрерывны функции такие, что . Площадь фигуры , ограниченной кривыми , , и прямыми вычисляется по формуле:

.

Площадь криволинейной трапеции, верхняя граница которой задана параметрическими уравнениями

, вычисляется по формуле:

.

Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением и двумя полярными радиусами, составляющими с полярной осью углы и , вычисляется по формуле:

.

Пример 4. Найти площадь плоской фигуры ограниченной линиями

х=0, у=4.

Решение. Будем иметь (ед²).

Пример 5. Найти площадь фигуры, ограниченной линиями

,

у

Решение.

х

3. Вычисление объёмов тел вращения .

Объём тела, полученного вращением вокруг оси Оx, криволинейной трапеции , определяется формулой

.

Пример 6. Найти объем тела, образованного вращением

фигуры, ограниченной линиями , , , х=1 вокруг оси Оx,

Решение.